Loading AI tools
Form of causal modeling that fit networks of constructs to data From Wikipedia, the free encyclopedia
Structural equation modeling (SEM) is a diverse set of methods used by scientists doing both observational and experimental research. SEM is used mostly in the social and behavioral sciences but it is also used in epidemiology,[2] business,[3] and other fields. A definition of SEM is difficult without reference to technical language, but a good starting place is the name itself.
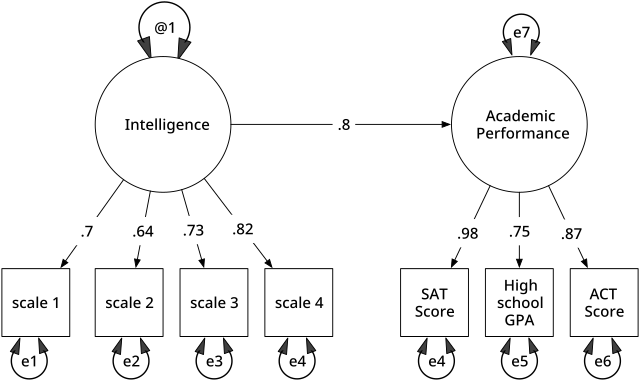
SEM involves a model representing how various aspects of some phenomenon are thought to causally connect to one another. Structural equation models often contain postulated causal connections among some latent variables (variables thought to exist but which can't be directly observed). Additional causal connections link those latent variables to observed variables whose values appear in a data set. The causal connections are represented using equations but the postulated structuring can also be presented using diagrams containing arrows as in Figures 1 and 2. The causal structures imply that specific patterns should appear among the values of the observed variables. This makes it possible to use the connections between the observed variables' values to estimate the magnitudes of the postulated effects, and to test whether or not the observed data are consistent with the requirements of the hypothesized causal structures.[4]
The boundary between what is and is not a structural equation model is not always clear but SE models often contain postulated causal connections among a set of latent variables (variables thought to exist but which can't be directly observed, like an attitude, intelligence or mental illness) and causal connections linking the postulated latent variables to variables that can be observed and whose values are available in some data set. Variations among the styles of latent causal connections, variations among the observed variables measuring the latent variables, and variations in the statistical estimation strategies result in the SEM toolkit including confirmatory factor analysis, confirmatory composite analysis, path analysis, multi-group modeling, longitudinal modeling, partial least squares path modeling, latent growth modeling and hierarchical or multilevel modeling.[5][6][7][8][9]
SEM researchers use computer programs to estimate the strength and sign of the coefficients corresponding to the modeled structural connections, for example the numbers connected to the arrows in Figure 1. Because a postulated model such as Figure 1 may not correspond to the worldly forces controlling the observed data measurements, the programs also provide model tests and diagnostic clues suggesting which indicators, or which model components, might introduce inconsistency between the model and observed data. Criticisms of SEM methods hint at: disregard of available model tests, problems in the model's specification, a tendency to accept models without considering external validity, and potential philosophical biases.[10]
A great advantage of SEM is that all of these measurements and tests occur simultaneously in one statistical estimation procedure, where all the model coefficients are calculated using all information from the observed variables. This means the estimates are more accurate than if a researcher were to calculate each part of the model separately.[11]
Structural equation modeling (SEM) began differentiating itself from correlation and regression when Sewall Wright provided explicit causal interpretations for a set of regression-style equations based on a solid understanding of the physical and physiological mechanisms producing direct and indirect effects among his observed variables.[12][13][14] The equations were estimated like ordinary regression equations but the substantive context for the measured variables permitted clear causal, not merely predictive, understandings. O. D. Duncan introduced SEM to the social sciences in his 1975 book[15] and SEM blossomed in the late 1970's and 1980's when increasing computing power permitted practical model estimation. In 1987 Hayduk[6] provided the first book-length introduction to structural equation modeling with latent variables, and this was soon followed by Bollen's popular text (1989).[16]
Different yet mathematically related modeling approaches developed in psychology, sociology, and economics. Early Cowles Commission work on simultaneous equations estimation centered on Koopman and Hood's (1953) algorithms from transport economics and optimal routing, with maximum likelihood estimation, and closed form algebraic calculations, as iterative solution search techniques were limited in the days before computers. The convergence of two of these developmental streams (factor analysis from psychology, and path analysis from sociology via Duncan) produced the current core of SEM. One of several programs Karl Jöreskog developed at Educational Testing Services, LISREL[17][18][19] embedded latent variables (which psychologists knew as the latent factors from factor analysis) within path-analysis-style equations (which sociologists inherited from Wright and Duncan). The factor-structured portion of the model incorporated measurement errors which permitted measurement-error-adjustment, though not necessarily error-free estimation, of effects connecting different postulated latent variables.
Traces of the historical convergence of the factor analytic and path analytic traditions persist as the distinction between the measurement and structural portions of models; and as continuing disagreements over model testing, and whether measurement should precede or accompany structural estimates.[20][21] Viewing factor analysis as a data-reduction technique deemphasizes testing, which contrasts with path analytic appreciation for testing postulated causal connections – where the test result might signal model misspecification. The friction between factor analytic and path analytic traditions continue to surface in the literature.
Wright's path analysis influenced Hermann Wold, Wold's student Karl Jöreskog, and Jöreskog's student Claes Fornell, but SEM never gained a large following among U.S. econometricians, possibly due to fundamental differences in modeling objectives and typical data structures. The prolonged separation of SEM's economic branch led to procedural and terminological differences, though deep mathematical and statistical connections remain.[22][23] The economic version of SEM can be seen in SEMNET discussions of endogeneity, and in the heat produced as Judea Pearl's approach to causality via directed acyclic graphs (DAG's) rubs against economic approaches to modeling.[4] Discussions comparing and contrasting various SEM approaches are available[24][25] but disciplinary differences in data structures and the concerns motivating economic models make reunion unlikely. Pearl[4] extended SEM from linear to nonparametric models, and proposed causal and counterfactual interpretations of the equations. Nonparametric SEMs permit estimating total, direct and indirect effects without making any commitment to linearity of effects or assumptions about the distributions of the error terms.[25]
SEM analyses are popular in the social sciences because computer programs make it possible to estimate complicated causal structures, but the complexity of the models introduces substantial variability in the quality of the results. Some, but not all, results are obtained without the "inconvenience" of understanding experimental design, statistical control, the consequences of sample size, and other features contributing to good research design.[citation needed]
The following considerations apply to the construction and assessment of many structural equation models.
Building or specifying a model requires attending to:
Structural equation models attempt to mirror the worldly forces operative for causally homogeneous cases – namely cases enmeshed in the same worldly causal structures but whose values on the causes differ and who therefore possess different values on the outcome variables. Causal homogeneity can be facilitated by case selection, or by segregating cases in a multi-group model. A model's specification is not complete until the researcher specifies:
The latent level of a model is composed of endogenous and exogenous variables. The endogenous latent variables are the true-score variables postulated as receiving effects from at least one other modeled variable. Each endogenous variable is modeled as the dependent variable in a regression-style equation. The exogenous latent variables are background variables postulated as causing one or more of the endogenous variables and are modeled like the predictor variables in regression-style equations. Causal connections among the exogenous variables are not explicitly modeled but are usually acknowledged by modeling the exogenous variables as freely correlating with one another. The model may include intervening variables – variables receiving effects from some variables but also sending effects to other variables. As in regression, each endogenous variable is assigned a residual or error variable encapsulating the effects of unavailable and usually unknown causes. Each latent variable, whether exogenous or endogenous, is thought of as containing the cases' true-scores on that variable, and these true-scores causally contribute valid/genuine variations into one or more of the observed/reported indicator variables.[26]
The LISREL program assigned Greek names to the elements in a set of matrices to keep track of the various model components. These names became relatively standard notation, though the notation has been extended and altered to accommodate a variety of statistical considerations.[19][6][16][27] Texts and programs "simplifying" model specification via diagrams or by using equations permitting user-selected variable names, re-convert the user's model into some standard matrix-algebra form in the background. The "simplifications" are achieved by implicitly introducing default program "assumptions" about model features with which users supposedly need not concern themselves. Unfortunately, these default assumptions easily obscure model components that leave unrecognized issues lurking within the model's structure, and underlying matrices.
Two main components of models are distinguished in SEM: the structural model showing potential causal dependencies between endogenous and exogenous latent variables, and the measurement model showing the causal connections between the latent variables and the indicators. Exploratory and confirmatory factor analysis models, for example, focus on the causal measurement connections, while path models more closely correspond to SEMs latent structural connections.
Modelers specify each coefficient in a model as being free to be estimated, or fixed at some value. The free coefficients may be postulated effects the researcher wishes to test, background correlations among the exogenous variables, or the variances of the residual or error variables providing additional variations in the endogenous latent variables. The fixed coefficients may be values like the 1.0 values in Figure 2 that provide a scales for the latent variables, or values of 0.0 which assert causal disconnections such as the assertion of no-direct-effects (no arrows) pointing from Academic Achievement to any of the four scales in Figure 1. SEM programs provide estimates and tests of the free coefficients, while the fixed coefficients contribute importantly to testing the overall model structure. Various kinds of constraints between coefficients can also be used.[27][6][16] The model specification depends on what is known from the literature, the researcher's experience with the modeled indicator variables, and the features being investigated by using the specific model structure.
There is a limit to how many coefficients can be estimated in a model. If there are fewer data points than the number of estimated coefficients, the resulting model is said to be "unidentified" and no coefficient estimates can be obtained. Reciprocal effect, and other causal loops, may also interfere with estimation.[28][29][27]
Model coefficients fixed at zero, 1.0, or other values, do not require estimation because they already have specified values. Estimated values for free model coefficients are obtained by maximizing fit to, or minimizing difference from, the data relative to what the data's features would be if the free model coefficients took on the estimated values. The model's implications for what the data should look like for a specific set of coefficient values depends on: a) the coefficients' locations in the model (e.g. which variables are connected/disconnected), b) the nature of the connections between the variables (covariances or effects; with effects often assumed to be linear), c) the nature of the error or residual variables (often assumed to be independent of, or causally-disconnected from, many variables), and d) the measurement scales appropriate for the variables (interval level measurement is often assumed).
A stronger effect connecting two latent variables implies the indicators of those latents should be more strongly correlated. Hence, a reasonable estimate of a latent's effect will be whatever value best matches the correlations between the indicators of the corresponding latent variables – namely the estimate-value maximizing the match with the data, or minimizing the differences from the data. With maximum likelihood estimation, the numerical values of all the free model coefficients are individually adjusted (progressively increased or decreased from initial start values) until they maximize the likelihood of observing the sample data – whether the data are the variables' covariances/correlations, or the cases' actual values on the indicator variables. Ordinary least squares estimates are the coefficient values that minimize the squared differences between the data and what the data would look like if the model was correctly specified, namely if all the model's estimated features correspond to real worldly features.
The appropriate statistical feature to maximize or minimize to obtain estimates depends on the variables' levels of measurement (estimation is generally easier with interval level measurements than with nominal or ordinal measures), and where a specific variable appears in the model (e.g. endogenous dichotomous variables create more estimation difficulties than exogenous dichotomous variables). Most SEM programs provide several options for what is to be maximized or minimized to obtain estimates the model's coefficients. The choices often include maximum likelihood estimation (MLE), full information maximum likelihood (FIML), ordinary least squares (OLS), weighted least squares (WLS), diagonally weighted least squares (DWLS), and two stage least squares.[27]
One common problem is that a coefficient's estimated value may be underidentified because it is insufficiently constrained by the model and data. No unique best-estimate exists unless the model and data together sufficiently constrain or restrict a coefficient's value. For example, the magnitude of a single data correlation between two variables is insufficient to provide estimates of a reciprocal pair of modeled effects between those variables. The correlation might be accounted for by one of the reciprocal effects being stronger than the other effect, or the other effect being stronger than the one, or by effects of equal magnitude. Underidentified effect estimates can be rendered identified by introducing additional model and/or data constraints. For example, reciprocal effects can be rendered identified by constraining one effect estimate to be double, triple, or equivalent to, the other effect estimate,[29] but the resultant estimates will only be trustworthy if the additional model constraint corresponds to the world's structure. Data on a third variable that directly causes only one of a pair of reciprocally causally connected variables can also assist identification.[28] Constraining a third variable to not directly cause one of the reciprocally-causal variables breaks the symmetry otherwise plaguing the reciprocal effect estimates because that third variable must be more strongly correlated with the variable it causes directly than with the variable at the "other" end of the reciprocal which it impacts only indirectly.[28] Notice that this again presumes the properness of the model's causal specification – namely that there really is a direct effect leading from the third variable to the variable at this end of the reciprocal effects and no direct effect on the variable at the "other end" of the reciprocally connected pair of variables. Theoretical demands for null/zero effects provide helpful constraints assisting estimation, though theories often fail to clearly report which effects are allegedly nonexistent.
 | This article may benefit from being shortened by the use of summary style. |
Model assessment depends on the theory, the data, the model, and the estimation strategy. Hence model assessments consider:
Research claiming to test or "investigate" a theory requires attending to beyond-chance model-data inconsistency. Estimation adjusts the model's free coefficients to provide the best possible fit to the data. The output from SEM programs includes a matrix reporting the relationships among the observed variables that would be observed if the estimated model effects actually controlled the observed variables' values. The "fit" of a model reports match or mismatch between the model-implied relationships (often covariances) and the corresponding observed relationships among the variables. Large and significant differences between the data and the model's implications signal problems. The probability accompanying a χ2 (chi-squared) test is the probability that the data could arise by random sampling variations if the estimated model constituted the real underlying population forces. A small χ2 probability reports it would be unlikely for the current data to have arisen if the modeled structure constituted the real population causal forces – with the remaining differences attributed to random sampling variations.
If a model remains inconsistent with the data despite selecting optimal coefficient estimates, an honest research response reports and attends to this evidence (often a significant model χ2 test).[30] Beyond-chance model-data inconsistency challenges both the coefficient estimates and the model's capacity for adjudicating the model's structure, irrespective of whether the inconsistency originates in problematic data, inappropriate statistical estimation, or incorrect model specification. Coefficient estimates in data-inconsistent ("failing") models are interpretable, as reports of how the world would appear to someone believing a model that conflicts with the available data. The estimates in data-inconsistent models do not necessarily become "obviously wrong" by becoming statistically strange, or wrongly signed according to theory. The estimates may even closely match a theory's requirements but the remaining data inconsistency renders the match between the estimates and theory unable to provide succor. Failing models remain interpretable, but only as interpretations that conflict with available evidence.
Replication is unlikely to detect misspecified models which inappropriately-fit the data. If the replicate data is within random variations of the original data, the same incorrect coefficient placements that provided inappropriate-fit to the original data will likely also inappropriately-fit the replicate data. Replication helps detect issues such as data mistakes (made by different research groups), but is especially weak at detecting misspecifications after exploratory model modification – as when confirmatory factor analysis (CFA) is applied to a random second-half of data following exploratory factor analysis (EFA) of first-half data.
A modification index is an estimate of how much a model's fit to the data would "improve" (but not necessarily how much the model's structure would improve) if a specific currently-fixed model coefficient were freed for estimation. Researchers confronting data-inconsistent models can easily free coefficients the modification indices report as likely to produce substantial improvements in fit. This simultaneously introduces a substantial risk of moving from a causally-wrong-and-failing model to a causally-wrong-but-fitting model because improved data-fit does not provide assurance that the freed coefficients are substantively reasonable or world matching. The original model may contain causal misspecifications such as incorrectly directed effects, or incorrect assumptions about unavailable variables, and such problems cannot be corrected by adding coefficients to the current model. Consequently, such models remain misspecified despite the closer fit provided by additional coefficients. Fitting yet worldly-inconsistent models are especially likely to arise if a researcher committed to a particular model (for example a factor model having a desired number of factors) gets an initially-failing model to fit by inserting measurement error covariances "suggested" by modification indices. MacCallum (1986) demonstrated that "even under favorable conditions, models arising from specification serchers must be viewed with caution."[31] Model misspecification may sometimes be corrected by insertion of coefficients suggested by the modification indices, but many more corrective possibilities are raised by employing a few indicators of similar-yet-importantly-different latent variables.[32]
"Accepting" failing models as "close enough" is also not a reasonable alternative. A cautionary instance was provided by Browne, MacCallum, Kim, Anderson, and Glaser who addressed the mathematics behind why the χ2 test can have (though it does not always have) considerable power to detect model misspecification.[33] The probability accompanying a χ2 test is the probability that the data could arise by random sampling variations if the current model, with its optimal estimates, constituted the real underlying population forces. A small χ2 probability reports it would be unlikely for the current data to have arisen if the current model structure constituted the real population causal forces – with the remaining differences attributed to random sampling variations. Browne, McCallum, Kim, Andersen, and Glaser presented a factor model they viewed as acceptable despite the model being significantly inconsistent with their data according to χ2. The fallaciousness of their claim that close-fit should be treated as good enough was demonstrated by Hayduk, Pazkerka-Robinson, Cummings, Levers and Beres[34] who demonstrated a fitting model for Browne, et al.'s own data by incorporating an experimental feature Browne, et al. overlooked. The fault was not in the math of the indices or in the over-sensitivity of χ2 testing. The fault was in Browne, MacCallum, and the other authors forgetting, neglecting, or overlooking, that the amount of ill fit cannot be trusted to correspond to the nature, location, or seriousness of problems in a model's specification.[35]
Many researchers tried to justify switching to fit-indices, rather than testing their models, by claiming that χ2 increases (and hence χ2 probability decreases) with increasing sample size (N). There are two mistakes in discounting χ2 on this basis. First, for proper models, χ2 does not increase with increasing N,[30] so if χ2 increases with N that itself is a sign that something is detectably problematic. And second, for models that are detectably misspecified, χ2 increase with N provides the good-news of increasing statistical power to detect model misspecification (namely power to detect Type II error). Some kinds of important misspecifications cannot be detected by χ2,[35] so any amount of ill fit beyond what might be reasonably produced by random variations warrants report and consideration.[36][30] The χ2 model test, possibly adjusted,[37] is the strongest available structural equation model test.
Numerous fit indices quantify how closely a model fits the data but all fit indices suffer from the logical difficulty that the size or amount of ill fit is not trustably coordinated with the severity or nature of the issues producing the data inconsistency.[35] Models with different causal structures which fit the data identically well, have been called equivalent models.[27] Such models are data-fit-equivalent though not causally equivalent, so at least one of the so-called equivalent models must be inconsistent with the world's structure. If there is a perfect 1.0 correlation between X and Y and we model this as X causes Y, there will be perfect fit and zero residual error. But the model may not match the world because Y may actually cause X, or both X and Y may be responding to a common cause Z, or the world may contain a mixture of these effects (e.g. like a common cause plus an effect of Y on X), or other causal structures. The perfect fit does not tell us the model's structure corresponds to the world's structure, and this in turn implies that getting closer to perfect fit does not necessarily correspond to getting closer to the world's structure – maybe it does, maybe it doesn't. This makes it incorrect for a researcher to claim that even perfect model fit implies the model is correctly causally specified. For even moderately complex models, precisely equivalently-fitting models are rare. Models almost-fitting the data, according to any index, unavoidably introduce additional potentially-important yet unknown model misspecifications. These models constitute a greater research impediment.
This logical weakness renders all fit indices "unhelpful" whenever a structural equation model is significantly inconsistent with the data,[36] but several forces continue to propagate fit-index use. For example, Dag Sorbom reported that when someone asked Karl Joreskog, the developer of the first structural equation modeling program, "Why have you then added GFI?" to your LISREL program, Joreskog replied "Well, users threaten us saying they would stop using LISREL if it always produces such large chi-squares. So we had to invent something to make people happy. GFI serves that purpose."[38] The χ2 evidence of model-data inconsistency was too statistically solid to be dislodged or discarded, but people could at least be provided a way to distract from the "disturbing" evidence. Career-profits can still be accrued by developing additional indices, reporting investigations of index behavior, and publishing models intentionally burying evidence of model-data inconsistency under an MDI (a mound of distracting indices). There seems no general justification for why a researcher should "accept" a causally wrong model, rather than attempting to correct detected misspecifications. And some portions of the literature seems not to have noticed that "accepting a model" (on the basis of "satisfying" an index value) suffers from an intensified version of the criticism applied to "acceptance" of a null-hypothesis. Introductory statistics texts usually recommend replacing the term "accept" with "failed to reject the null hypothesis" to acknowledge the possibility of Type II error. A Type III error arises from "accepting" a model hypothesis when the current data are sufficient to reject the model.
Whether or not researchers are committed to seeking the world’s structure is a fundamental concern. Displacing test evidence of model-data inconsistency by hiding it behind index claims of acceptable-fit, introduces the discipline-wide cost of diverting attention away from whatever the discipline might have done to attain a structurally-improved understanding of the discipline’s substance. The discipline ends up paying a real costs for index-based displacement of evidence of model misspecification. The frictions created by disagreements over the necessity of correcting model misspecifications will likely increase with increasing use of non-factor-structured models, and with use of fewer, more-precise, indicators of similar yet importantly-different latent variables.[32]
The considerations relevant to using fit indices include checking:
Some of the more commonly used fit statistics include
The following table provides references documenting these, and other, features for some common indices: the RMSEA (Root Mean Square Error of Approximation), SRMR (Standardized Root Mean Squared Residual), CFI (Confirmatory Fit Index), and the TLI (the Tucker-Lewis Index). Additional indices such as the AIC (Akaike Information Criterion) can be found in most SEM introductions.[27] For each measure of fit, a decision as to what represents a good-enough fit between the model and the data reflects the researcher's modeling objective (perhaps challenging someone else's model, or improving measurement); whether or not the model is to be claimed as having been "tested"; and whether the researcher is comfortable "disregarding" evidence of the index-documented degree of ill fit.[30]
| RMSEA | SRMR | CFI | |
|---|---|---|---|
| Index Name | Root Mean Square Error of Approximation | Standardized Root Mean Squared Residual | Confirmatory Fit Index |
| Formula | RMSEA = sq-root((χ2 - d)/(d(N-1))) | ||
| Basic References | [43][44][45] | ||
| Factor Model proposed wording
for critical values |
.06 wording?[39] | ||
| NON-Factor Model proposed wording
for critical values |
|||
| References proposing revised/changed, disagreements over critical values |
[39] | [39] | [39] |
| References indicating two-index or paired-index
criteria are required |
[39] | [39] | [39] |
| Index based on χ2 | Yes | No | Yes |
| References recommending against use
of this index |
[36] | [36] | [36] |
Researchers agree samples should be large enough to provide stable coefficient estimates and reasonable testing power but there is no general consensus regarding specific required sample sizes, or even how to determine appropriate sample sizes. Recommendations have been based on the number of coefficients to be estimated, the number of modeled variables, and Monte Carlo simulations addressing specific model coefficients.[27] Sample size recommendations based on the ratio of the number of indicators to latents are factor oriented and do not apply to models employing single indicators having fixed nonzero measurement error variances.[32] Overall, for moderate sized models without statistically difficult-to-estimate coefficients, the required sample sizes (N’s) seem roughly comparable to the N’s required for a regression employing all the indicators.
The larger the sample size, the greater the likelihood of including cases that are not causally homogeneous. Consequently, increasing N to improve the likelihood of being able to report a desired coefficient as statistically significant, simultaneously increases the risk of model misspecification, and the power to detect the misspecification. Researchers seeking to learn from their modeling (including potentially learning their model requires adjustment or replacement) will strive for as large a sample size as permitted by funding and by their assessment of likely population-based causal heterogeneity/homogeneity. If the available N is huge, modeling sub-sets of cases can control for variables that might otherwise disrupt causal homogeneity. Researchers fearing they might have to report their model’s deficiencies are torn between wanting a larger N to provide sufficient power to detect structural coefficients of interest, while avoiding the power capable of signaling model-data inconsistency. The huge variation in model structures and data characteristics suggests adequate sample sizes might be usefully located by considering other researchers’ experiences (both good and bad) with models of comparable size and complexity that have been estimated with similar data.
Causal interpretations of SE models are the clearest and most understandable but those interpretations will be fallacious/wrong if the model’s structure does not correspond to the world’s causal structure. Consequently, interpretation should address the overall status and structure of the model, not merely the model’s estimated coefficients. Whether a model fits the data, and/or how a model came to fit the data, are paramount for interpretation. Data fit obtained by exploring, or by following successive modification indices, does not guarantee the model is wrong but raises serious doubts because these approaches are prone to incorrectly modeling data features. For example, exploring to see how many factors are required preempts finding the data are not factor structured, especially if the factor model has been “persuaded” to fit via inclusion of measurement error covariances. Data’s ability to speak against a postulated model is progressively eroded with each unwarranted inclusion of a “modification index suggested” effect or error covariance. It becomes exceedingly difficult to recover a proper model if the initial/base model contains several misspecifications.[46]
Direct-effect estimates are interpreted in parallel to the interpretation of coefficients in regression equations but with causal commitment. Each unit increase in a causal variable’s value is viewed as producing a change of the estimated magnitude in the dependent variable’s value given control or adjustment for all the other operative/modeled causal mechanisms. Indirect effects are interpreted similarly, with the magnitude of a specific indirect effect equaling the product of the series of direct effects comprising that indirect effect. The units involved are the real scales of observed variables’ values, and the assigned scale values for latent variables. A specified/fixed 1.0 effect of a latent on a specific indicator coordinates that indicator’s scale with the latent variable’s scale. The presumption that the remainder of the model remains constant or unchanging may require discounting indirect effects that might, in the real world, be simultaneously prompted by a real unit increase. And the unit increase itself might be inconsistent with what is possible in the real world because there may be no known way to change the causal variable’s value. If a model adjusts for measurement errors, the adjustment permits interpreting latent-level effects as referring to variations in true scores.[26]
SEM interpretations depart most radically from regression interpretations when a network of causal coefficients connects the latent variables because regressions do not contain estimates of indirect effects. SEM interpretations should convey the consequences of the patterns of indirect effects that carry effects from background variables through intervening variables to the downstream dependent variables. SEM interpretations encourage understanding how multiple worldly causal pathways can work in coordination, or independently, or even counteract one another. Direct effects may be counteracted (or reinforced) by indirect effects, or have their correlational implications counteracted (or reinforced) by the effects of common causes.[15] The meaning and interpretation of specific estimates should be contextualized in the full model.
SE model interpretation should connect specific model causal segments to their variance and covariance implications. A single direct effect reports that the variance in the independent variable produces a specific amount of variation in the dependent variable’s values, but the causal details of precisely what makes this happens remains unspecified because a single effect coefficient does not contain sub-components available for integration into a structured story of how that effect arises. A more fine-grained SE model incorporating variables intervening between the cause and effect would be required to provide features constituting a story about how any one effect functions. Until such a model arrives each estimated direct effect retains a tinge of the unknown, thereby invoking the essence of a theory. A parallel essential unknownness would accompany each estimated coefficient in even the more fine-grained model, so the sense of fundamental mystery is never fully eradicated from SE models.
Even if each modeled effect is unknown beyond the identity of the variables involved and the estimated magnitude of the effect, the structures linking multiple modeled effects provide opportunities to express how things function to coordinate the observed variables – thereby providing useful interpretation possibilities. For example, a common cause contributes to the covariance or correlation between two effected variables, because if the value of the cause goes up, the values of both effects should also go up (assuming positive effects) even if we do not know the full story underlying each cause.[15] (A correlation is the covariance between two variables that have both been standardized to have variance 1.0). Another interpretive contribution might be made by expressing how two causal variables can both explain variance in a dependent variable, as well as how covariance between two such causes can increase or decrease explained variance in the dependent variable. That is, interpretation may involve explaining how a pattern of effects and covariances can contribute to decreasing a dependent variable’s variance.[47] Understanding causal implications implicitly connects to understanding “controlling”, and potentially explaining why some variables, but not others, should be controlled.[4][48] As models become more complex these fundamental components can combine in non-intuitive ways, such as explaining how there can be no correlation (zero covariance) between two variables despite the variables being connected by a direct non-zero causal effect.[15][16][6][29]
The statistical insignificance of an effect estimate indicates the estimate could rather easily arise as a random sampling variation around a null/zero effect, so interpreting the estimate as a real effect becomes equivocal. As in regression, the proportion of each dependent variable’s variance explained by variations in the modeled causes are provided by R2, though the Blocked-Error R2 should be used if the dependent variable is involved in reciprocal or looped effects, or if it has an error variable correlated with any predictor’s error variable.[49]
The caution appearing in the Model Assessment section warrants repeat. Interpretation should be possible whether a model is or is not consistent with the data. The estimates report how the world would appear to someone believing the model – even if that belief is unfounded because the model happens to be wrong. Interpretation should acknowledge that the model coefficients may or may not correspond to “parameters” – because the model’s coefficients may not have corresponding worldly structural features.
Adding new latent variables entering or exiting the original model at a few clear causal locations/variables contributes to detecting model misspecifications which could otherwise ruin coefficient interpretations. The correlations between the new latent’s indicators and all the original indicators contribute to testing the original model’s structure because the few new and focused effect coefficients must work in coordination with the model’s original direct and indirect effects to coordinate the new indicators with the original indicators. If the original model’s structure was problematic, the sparse new causal connections will be insufficient to coordinate the new indicators with the original indicators, thereby signaling the inappropriateness of the original model’s coefficients through model-data inconsistency.[29] The correlational constraints grounded in null/zero effect coefficients, and coefficients assigned fixed nonzero values, contribute to both model testing and coefficient estimation, and hence deserve acknowledgment as the scaffolding supporting the estimates and their interpretation.[29]
Interpretations become progressively more complex for models containing interactions, nonlinearities, multiple groups, multiple levels, and categorical variables.[27] Effects touching causal loops, reciprocal effects, or correlated residuals also require slightly revised interpretations.[6][29]
Careful interpretation of both failing and fitting models can provide research advancement. To be dependable, the model should investigate academically informative causal structures, fit applicable data with understandable estimates, and not include vacuous coefficients.[50] Dependable fitting models are rarer than failing models or models inappropriately bludgeoned into fitting, but appropriately-fitting models are possible.[34][51][52][53]
The multiple ways of conceptualizing PLS models[54] complicate interpretation of PLS models. Many of the above comments are applicable if a PLS modeler adopts a realist perspective by striving to ensure their modeled indicators combine in a way that matches some existing but unavailable latent variable. Non-causal PLS models, such as those focusing primarily on R2 or out-of-sample predictive power, change the interpretation criteria by diminishing concern for whether or not the model’s coefficients have worldly counterparts. The fundamental features differentiating the five PLS modeling perspectives discussed by Rigdon, Sarstedt and Ringle[54] point to differences in PLS modelers’ objectives, and corresponding differences in model features warranting interpretation.
Caution should be taken when making claims of causality even when experiments or time-ordered investigations have been undertaken. The term causal model must be understood to mean "a model that conveys causal assumptions", not necessarily a model that produces validated causal conclusions—maybe it does maybe it does not. Collecting data at multiple time points and using an experimental or quasi-experimental design can help rule out certain rival hypotheses but even a randomized experiments cannot fully rule out threats to causal claims. No research design can fully guarantee causal structures.[4]
Structural equation modeling is fraught with controversies. Researchers from the factor analytic tradition commonly attempt to reduce sets of multiple indicators to fewer, more manageable, scales or factor-scores for later use in path-structured models. This constitutes a stepwise process with the initial measurement step providing scales or factor-scores which are to be used later in a path-structured model. This stepwise approach seems obvious but actually confronts severe underlying deficiencies. The segmentation into steps interferes with thorough checking of whether the scales or factor-scores validly represent the indicators, and/or validly report on latent level effects. A structural equation model simultaneously incorporating both the measurement and latent-level structures not only checks whether the latent factors appropriately coordinates the indicators, it also checks whether that same latent simultaneously appropriately coordinates each latent’s indictors with the indicators of theorized causes and/or consequences of that latent.[29] If a latent is unable to do both these styles of coordination, the validity of that latent is questioned, and a scale or factor-scores purporting to measure that latent is questioned. The disagreements swirled around respect for, or disrespect of, evidence challenging the validity of postulated latent factors. The simmering, sometimes boiling, discussions resulted in a special issue of the journal Structural Equation Modeling focused on a target article by Hayduk and Glaser[20] followed by several comments and a rejoinder,[21] all made freely available, thanks to the efforts of George Marcoulides.
These discussions fueled disagreement over whether or not structural equation models should be tested for consistency with the data, and model testing became the next focus of discussions. Scholars having path-modeling histories tended to defend careful model testing while those with factor-histories tended to defend fit-indexing rather than fit-testing. These discussions led to a target article in Personality and Individual Differences by Paul Barrett[36] who said: “In fact, I would now recommend banning ALL such indices from ever appearing in any paper as indicative of model “acceptability” or “degree of misfit”.” [36](page 821). Barrett’s article was also accompanied by commentary from both perspectives.[50][55]
The controversy over model testing declined as clear reporting of significant model-data inconsistency becomes mandatory. Scientists do not get to ignore, or fail to report, evidence just because they do not like what the evidence reports.[30] The requirement of attending to evidence pointing toward model mis-specification underpins more recent concern for addressing “endogeneity” – a style of model mis-specification that interferes with estimation due to lack of independence of error/residual variables. In general, the controversy over the causal nature of structural equation models, including factor-models, has also been declining. Stan Mulaik, a factor-analysis stalwart, has acknowledged the causal basis of factor models.[56] The comments by Bollen and Pearl regarding myths about causality in the context of SEM[25] reinforced the centrality of causal thinking in the context of SEM.
A briefer controversy focused on competing models. Comparing competing models can be very helpful but there are fundamental issues that cannot be resolved by creating two models and retaining the better fitting model. The statistical sophistication of presentations like Levy and Hancock (2007),[57] for example, makes it easy to overlook that a researcher might begin with one terrible model and one atrocious model, and end by retaining the structurally terrible model because some index reports it as better fitting than the atrocious model. It is unfortunate that even otherwise strong SEM texts like Kline (2016)[27] remain disturbingly weak in their presentation of model testing.[58] Overall, the contributions that can be made by structural equation modeling depend on careful and detailed model assessment, even if a failing model happens to be the best available.
An additional controversy that touched the fringes of the previous controversies awaits ignition.[citation needed] Factor models and theory-embedded factor structures having multiple indicators tend to fail, and dropping weak indicators tends to reduce the model-data inconsistency. Reducing the number of indicators leads to concern for, and controversy over, the minimum number of indicators required to support a latent variable in a structural equation model. Researchers tied to factor tradition can be persuaded to reduce the number of indicators to three per latent variable, but three or even two indicators may still be inconsistent with a proposed underlying factor common cause. Hayduk and Littvay (2012)[32] discussed how to think about, defend, and adjust for measurement error, when using only a single indicator for each modeled latent variable. Single indicators have been used effectively in SE models for a long time,[51] but controversy remains only as far away as a reviewer who has considered measurement from only the factor analytic perspective.
Though declining, traces of these controversies are scattered throughout the SEM literature, and you can easily incite disagreement by asking: What should be done with models that are significantly inconsistent with the data? Or by asking: Does model simplicity override respect for evidence of data inconsistency? Or, what weight should be given to indexes which show close or not-so-close data fit for some models? Or, should we be especially lenient toward, and “reward”, parsimonious models that are inconsistent with the data? Or, given that the RMSEA condones disregarding some real ill fit for each model degree of freedom, doesn’t that mean that people testing models with null-hypotheses of non-zero RMSEA are doing deficient model testing? Considerable variation in statistical sophistication is required to cogently address such questions, though responses will likely center on the non-technical matter of whether or not researchers are required to report and respect evidence.
Structural equation modeling programs differ widely in their capabilities and user requirements.[66]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
