Tetrahedron

Not to be confused with Tetraedron or Tetrahedron (journal).

In geometry, a tetrahedron (pl.: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra.^[1]

The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex.

The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid".

Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.^[1]

For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere (the insphere) tangent to the tetrahedron's faces.^[2]

Regular tetrahedron

A regular tetrahedron and its net

A regular tetrahedron is a tetrahedron in which all four faces are equilateral triangles. In other words, all of its faces are the same size and shape (congruent) and all edges are the same length. The regular tetrahedron is the simplest convex deltahedron, a polyhedron in which all of its faces are equilateral triangles; there are seven other convex deltahedra.^[3]

Regular tetrahedron, described as the classical element of fire.

The regular tetrahedron is also one of the five regular Platonic solids, a set of polyhedra in which all of their faces are regular polygons.^[4] Known since antiquity, the Platonic solid is named after the Greek philosopher Plato, who associated those four solids with nature. The regular tetrahedron was considered the classical element of fire, because of his interpretation of its sharpest corner being most penetrating.^[5]

The regular tetrahedron is self-dual, meaning its dual is another regular tetrahedron.

Measurement

3D model of a regular tetrahedron

Consider a regular tetrahedron with edge length ${\displaystyle a}$. Its height is ${\textstyle {{\sqrt {\frac {2}{3}}}a}}$.^[6] Its surface area is four times the area of an equilateral triangle: ${\textstyle A=4\cdot \left({\frac {\sqrt {3}}{4}}a^{2}\right)=a^{2}{\sqrt {3}}\approx 1.732a^{2}.}$^[7] The volume is one-third of the base times the height, the general formula for a pyramid;^[7] this can also be found by dissecting a cube into a tetrahedron and four triangular pyramids.^[8] $${\displaystyle V={\frac {1}{3}}\cdot \left({\frac {\sqrt {3}}{4}}a^{2}\right)\cdot {\frac {\sqrt {6}}{3}}a={\frac {a^{3}}{6{\sqrt {2}}}}\approx 0.118a^{3}.}$$

Its dihedral angle—the angle formed by two planes in which adjacent faces lie—is ${\textstyle \arccos \left(1/3\right)=\arctan \left(2{\sqrt {2}}\right)\approx 70.529^{\circ }.}$^[7]

The radii of its circumsphere ${\displaystyle R}$, insphere ${\displaystyle r}$, midsphere ${\displaystyle r_{\mathrm {M} }}$, and exsphere ${\displaystyle r_{\mathrm {E} }}$ are:^[7] $${\displaystyle {\begin{aligned}R={\sqrt {\frac {3}{8}}}a,&\qquad r={\frac {1}{3}}R={\frac {a}{\sqrt {24}}},\\r_{\mathrm {M} }={\sqrt {rR}}={\frac {a}{\sqrt {8}}},&\qquad r_{\mathrm {E} }={\frac {a}{\sqrt {6}}}.\end{aligned}}}$$ For a regular tetrahedron with side length ${\displaystyle a}$ and circumsphere radius ${\displaystyle R}$, the distances ${\displaystyle d_{i}}$ from an arbitrary point in 3-space to its four vertices satisfy the equations:^[9] $${\displaystyle {\begin{aligned}{\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+{\frac {16R^{4}}{9}}&=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+{\frac {2R^{2}}{3}}\right)^{2},\\4\left(a^{4}+d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}\right)&=\left(a^{2}+d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}\right)^{2}.\end{aligned}}}$$

With respect to the base plane the slope of a face (2√2) is twice that of an edge (√2), corresponding to the fact that the horizontal distance covered from the base to the apex along an edge is twice that along the median of a face. In other words, if C is the centroid of the base, the distance from C to a vertex of the base is twice that from C to the midpoint of an edge of the base. This follows from the fact that the medians of a triangle intersect at its centroid, and this point divides each of them in two segments, one of which is twice as long as the other (see proof).

Its solid angle at a vertex subtended by a face is ${\textstyle \arccos \left({\frac {23}{27}}\right)={\frac {\pi }{2}}-3\arcsin \left({\frac {1}{3}}\right)=3\arccos \left({\frac {1}{3}}\right)-\pi ,}$ or approximately 0.55129 steradians, 1809.8 square degrees, and 0.04387 spats.

Cartesian coordinates

One way to construct a regular tetrahedron is by using the following Cartesian coordinates, defining the four vertices of a tetrahedron with edge length 2, centered at the origin, and two-level edges: $${\displaystyle \left(\pm 1,0,-{\frac {1}{\sqrt {2}}}\right)\quad {\mbox{and}}\quad \left(0,\pm 1,{\frac {1}{\sqrt {2}}}\right)}$$

Expressed symmetrically as 4 points on the unit sphere, centroid at the origin, with lower face parallel to the ${\displaystyle xy}$ plane, the vertices are: $${\displaystyle {\begin{aligned}\left({\sqrt {\frac {8}{9}}},0,-{\frac {1}{3}}\right),&\quad \left(-{\sqrt {\frac {2}{9}}},{\sqrt {\frac {2}{3}}},-{\frac {1}{3}}\right),\\\left(-{\sqrt {\frac {2}{9}}},-{\sqrt {\frac {2}{3}}},-{\frac {1}{3}}\right),&\quad (0,0,1)\end{aligned}}}$$ with the edge length of ${\textstyle {\frac {2{\sqrt {6}}}{3}}}$.

A regular tetrahedron can be embedded inside a cube in two ways such that each vertex is a vertex of the cube, and each edge is a diagonal of one of the cube's faces. For one such embedding, the Cartesian coordinates of the vertices are $${\displaystyle {\begin{aligned}(1,1,1),&\quad (1,-1,-1),\\(-1,1,-1),&\quad (-1,-1,1).\end{aligned}}}$$ This yields a tetrahedron with edge-length ${\displaystyle 2{\sqrt {2}}}$, centered at the origin. For the other tetrahedron (which is dual to the first), reverse all the signs. These two tetrahedra's vertices combined are the vertices of a cube, demonstrating that the regular tetrahedron is the 3-demicube, a polyhedron that is by alternating a cube. This form has Coxeter diagram and Schläfli symbol ${\displaystyle \mathrm {h} \{4,3\}}$.

Symmetry

Main article: Tetrahedral symmetry

The cube and tetrahedron

The proper rotations, (order-3 rotation on a vertex and face, and order-2 on two edges) and reflection plane (through two faces and one edge) in the symmetry group of the regular tetrahedron

The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron, showing one of the two tetrahedra in the cube. The symmetries of a regular tetrahedron correspond to half of those of a cube: those that map the tetrahedra to themselves, and not to each other. The tetrahedron is the only Platonic solid not mapped to itself by point inversion.

The regular tetrahedron has 24 isometries, forming the symmetry group known as full tetrahedral symmetry ${\displaystyle \mathrm {T} _{\mathrm {d} }}$, which is isomorphic to the symmetric group ${\displaystyle S_{4}}$. This point group has rotational tetrahedral symmetry ${\displaystyle \mathrm {T} }$, which is isomorphic to alternating group ${\displaystyle A_{4}}$ (the identity and 11 proper rotations); six reflections in a plane perpendicular to an edge, six reflections in a plane combined with 90° rotation about an axis perpendicular to the plane, consisted of three axes, two per axis, together six (equivalently, they are 90° rotations combined with inversion).

Orthogonal projections of the regular tetrahedron

The regular tetrahedron has two special orthogonal projections, one centered on a vertex or equivalently on a face, and one centered on an edge. The first corresponds to the A₂ Coxeter plane.

Orthographic projection

Centered by	Face/vertex	Edge
Image
Projective symmetry	[3]	[4]

Cross section of regular tetrahedron

A central cross section of a regular tetrahedron is a square.

The two skew perpendicular opposite edges of a regular tetrahedron define a set of parallel planes. When one of these planes intersects the tetrahedron the resulting cross section is a rectangle.^[10] When the intersecting plane is near one of the edges the rectangle is long and skinny. When halfway between the two edges the intersection is a square. The aspect ratio of the rectangle reverses as you pass this halfway point. For the midpoint square intersection the resulting boundary line traverses every face of the tetrahedron similarly. If the tetrahedron is bisected on this plane, both halves become wedges.

A tetragonal disphenoid viewed orthogonally to the two green edges.

This property also applies for tetragonal disphenoids when applied to the two special edge pairs.

Spherical tiling

The tetrahedron can also be represented as a spherical tiling (of spherical triangles), and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Orthographic projection	Stereographic projection

Helical stacking

A single 30-tetrahedron ring Boerdijk–Coxeter helix within the 600-cell, seen in stereographic projection

Regular tetrahedra can be stacked face-to-face in a chiral aperiodic chain called the Boerdijk–Coxeter helix.

In four dimensions, all the convex regular 4-polytopes with tetrahedral cells (the 5-cell, 16-cell and 600-cell) can be constructed as tilings of the 3-sphere by these chains, which become periodic in the three-dimensional space of the 4-polytope's boundary surface.

Related figures

Compounds of tetrahedra

Left to right: compound of two tetrahedra, compound of five tetrahedra, compound of ten tetrahedra

The stellated octahedron is constructed by extending its faces to form equilateral triangles on each regular octahedron's face. In the perspective of polyhedral compounds, this figure comprises two such dual tetrahedra,^[11] a self-dual because of sharing a common intersphere in the center.^[12] Another interesting polyhedral compound involves five intersecting tetrahedra, which has been known for hundreds of years. It comes up regularly in the world of origami. Joining the twenty vertices would form a regular dodecahedron. There are both left-handed and right-handed forms, which are mirror images of each other. Superimposing both forms gives a compound of ten tetrahedra, in which the ten tetrahedra are arranged as five pairs of stellae octangulae.

Truncated tetrahedron and its dual, the triakis tetrahedron

Many polyhedra are constructed involving regular tetrahedra. By truncating the vertices of a regular tetrahedron, it becomes a truncated tetrahedron.^[13] The dual of this solid is the triakis tetrahedron, a regular tetrahedron with four triangular pyramids attached to each of its faces. i.e., its Kleetope.^[14] Some Johnson solid such as elongated triangular pyramid and elongated triangular bipyramid are constructed by attaching one and two regular tetrahedra onto the bases of a triangular prism; the triangular bipyramid is constructed by attaching two regular tetrahedra face-to-face.^[15]

Regular tetrahedron is the degenerated antiprism.^[16]

Pentachoron as the generalization of a four-dimensional tetrahedron

The pentachoron is a four-dimensional polytope, a generalization of a tetrahedron in four-dimensional space. It is bounded by five regular tetrahedra, known as cells.^[17]

Five tetrahedra are laid flat on a plane, with the highest 3-dimensional points marked as 1, 2, 3, 4, and 5. These points are then attached and a thin volume of an empty space is left, where the five edge angles do not quite meet.

Regular tetrahedra alone do not tessellate (fill space), but if alternated with regular octahedra in the ratio of two tetrahedra to one octahedron, they form the alternated cubic honeycomb, which is a tessellation. Some tetrahedra that are not regular, including the Schläfli orthoscheme and the Hill tetrahedron, can tessellate.

Irregular tetrahedra

If all three pairs of opposite edges of a tetrahedron are perpendicular, then it is called an orthocentric tetrahedron. When only one pair of opposite edges are perpendicular, it is called a semi-orthocentric tetrahedron. In a trirectangular tetrahedron the three face angles at one vertex are right angles, as at the corner of a cube.

An isodynamic tetrahedron is one in which the cevians that join the vertices to the incenters of the opposite faces are concurrent.

An isogonic tetrahedron has concurrent cevians that join the vertices to the points of contact of the opposite faces with the inscribed sphere of the tetrahedron.

Disphenoid

Main article: Disphenoid

A space-filling tetrahedral disphenoid inside a cube. Two edges have dihedral angles of 90°, and four edges have dihedral angles of 60°.

A disphenoid is a tetrahedron with four congruent triangles as faces; the triangles necessarily have all angles acute. The regular tetrahedron is a special case of a disphenoid. Other names for the same shape include bisphenoid, isosceles tetrahedron and equifacial tetrahedron.

Orthoschemes

A cube dissected into six characteristic orthoschemes.

A 3-orthoscheme is a tetrahedron where all four faces are right triangles. A 3-orthoscheme is not a disphenoid, because its opposite edges are not of equal length. It is not possible to construct a disphenoid with right triangle or obtuse triangle faces.

An orthoscheme is an irregular simplex that is the convex hull of a tree in which all edges are mutually perpendicular. In a 3-dimensional orthoscheme, the tree consists of three perpendicular edges connecting all four vertices in a linear path that makes two right-angled turns. The 3-orthoscheme is a tetrahedron having two right angles at each of two vertices, so another name for it is birectangular tetrahedron. It is also called a quadrirectangular tetrahedron because it contains four right angles.^[18]

Coxeter also calls quadrirectangular tetrahedra "characteristic tetrahedra", because of their integral relationship to the regular polytopes and their symmetry groups.^[19] For example, the special case of a 3-orthoscheme with equal-length perpendicular edges is characteristic of the cube, which means that the cube can be subdivided into instances of this orthoscheme. If its three perpendicular edges are of unit length, its remaining edges are two of length √2 and one of length √3, so all its edges are edges or diagonals of the cube. The cube can be dissected into six such 3-orthoschemes four different ways, with all six surrounding the same √3 cube diagonal. The cube can also be dissected into 48 smaller instances of this same characteristic 3-orthoscheme (just one way, by all of its symmetry planes at once). The characteristic tetrahedron of the cube is an example of a Heronian tetrahedron.

Every regular polytope, including the regular tetrahedron, has its characteristic orthoscheme. There is a 3-orthoscheme, which is the "characteristic tetrahedron of the regular tetrahedron". The regular tetrahedron is subdivided into 24 instances of its characteristic tetrahedron by its planes of symmetry. The 24 characteristic tetrahedra of the regular tetrahedron occur in two mirror-image forms, 12 of each.

Characteristics of the regular tetrahedron[20]
	edge	arc		dihedral
𝒍	${\displaystyle 2}$	109°28′16″	${\displaystyle \pi -2\kappa }$	70°31′44″	${\displaystyle \pi -2\psi }$
𝟀	${\displaystyle {\sqrt {\tfrac {4}{3}}}\approx 1.155}$	70°31′44″	${\displaystyle 2\kappa }$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
𝝉[a]	${\displaystyle 1}$	54°44′8″	${\displaystyle {\tfrac {\pi }{2}}-\kappa }$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
𝟁	${\displaystyle {\sqrt {\tfrac {1}{3}}}\approx 0.577}$	54°44′8″	${\displaystyle {\tfrac {\pi }{2}}-\kappa }$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
${\displaystyle _{0}R/l}$	${\displaystyle {\sqrt {\tfrac {3}{2}}}\approx 1.225}$
${\displaystyle _{1}R/l}$	${\displaystyle {\sqrt {\tfrac {1}{2}}}\approx 0.707}$
${\displaystyle _{2}R/l}$	${\displaystyle {\sqrt {\tfrac {1}{6}}}\approx 0.408}$
${\displaystyle \kappa }$		35°15′52″	${\displaystyle {\tfrac {{\text{arc sec }}3}{2}}}$

If the regular tetrahedron has edge length 𝒍 = 2, its characteristic tetrahedron's six edges have lengths ${\displaystyle {\sqrt {\tfrac {4}{3}}}}$, ${\displaystyle 1}$, ${\displaystyle {\sqrt {\tfrac {1}{3}}}}$ around its exterior right-triangle face (the edges opposite the characteristic angles 𝟀, 𝝉, 𝟁),^[a] plus ${\displaystyle {\sqrt {\tfrac {3}{2}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{2}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{6}}}}$ (edges that are the characteristic radii of the regular tetrahedron). The 3-edge path along orthogonal edges of the orthoscheme is ${\displaystyle 1}$, ${\displaystyle {\sqrt {\tfrac {1}{3}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{6}}}}$, first from a tetrahedron vertex to an tetrahedron edge center, then turning 90° to an tetrahedron face center, then turning 90° to the tetrahedron center. The orthoscheme has four dissimilar right triangle faces. The exterior face is a 60-90-30 triangle which is one-sixth of a tetrahedron face. The three faces interior to the tetrahedron are: a right triangle with edges ${\displaystyle 1}$, ${\displaystyle {\sqrt {\tfrac {3}{2}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{2}}}}$, a right triangle with edges ${\displaystyle {\sqrt {\tfrac {1}{3}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{2}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{6}}}}$, and a right triangle with edges ${\displaystyle {\sqrt {\tfrac {4}{3}}}}$, ${\displaystyle {\sqrt {\tfrac {3}{2}}}}$, ${\displaystyle {\sqrt {\tfrac {1}{6}}}}$.

Space-filling tetrahedra

A space-filling tetrahedron packs with directly congruent or enantiomorphous (mirror image) copies of itself to tile space.^[21] The cube can be dissected into six 3-orthoschemes, three left-handed and three right-handed (one of each at each cube face), and cubes can fill space, so the characteristic 3-orthoscheme of the cube is a space-filling tetrahedron in this sense. (The characteristic orthoscheme of the cube is one of the Hill tetrahedra, a family of space-filling tetrahedra. All space-filling tetrahedra are scissors-congruent to a cube.)

A disphenoid can be a space-filling tetrahedron in the directly congruent sense, as in the disphenoid tetrahedral honeycomb. Regular tetrahedra, however, cannot fill space by themselves (moreover, it is not scissors-congruent to any other polyhedra which can fill the space, see Hilbert's third problem). The tetrahedral-octahedral honeycomb fills space with alternating regular tetrahedron cells and regular octahedron cells in a ratio of 2:1.

Fundamental domains

For Euclidean 3-space, there are 3 simple and related Goursat tetrahedra. They can be seen as points on and within a cube.

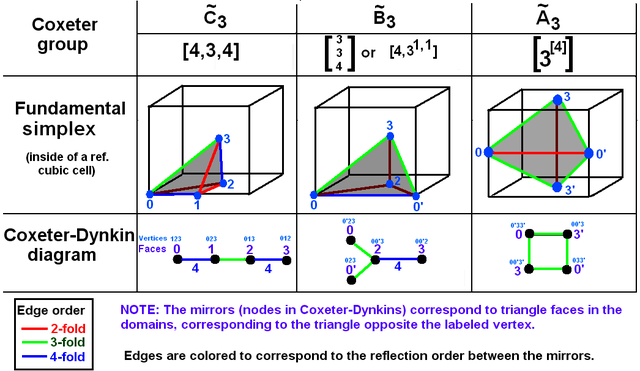
An irregular tetrahedron which is the fundamental domain^[22] of a symmetry group is an example of a Goursat tetrahedron. The Goursat tetrahedra generate all the regular polyhedra (and many other uniform polyhedra) by mirror reflections, a process referred to as Wythoff's kaleidoscopic construction.

For polyhedra, Wythoff's construction arranges three mirrors at angles to each other, as in a kaleidoscope. Unlike a cylindrical kaleidoscope, Wythoff's mirrors are located at three faces of a Goursat tetrahedron such that all three mirrors intersect at a single point. (The Coxeter-Dynkin diagram of the generated polyhedron contains three nodes representing the three mirrors. The dihedral angle between each pair of mirrors is encoded in the diagram, as well as the location of a single generating point which is multiplied by mirror reflections into the vertices of the polyhedron.)

Among the Goursat tetrahedra which generate 3-dimensional honeycombs we can recognize an orthoscheme (the characteristic tetrahedron of the cube), a double orthoscheme (the characteristic tetrahedron of the cube face-bonded to its mirror image), and the space-filling disphenoid illustrated above.^[19] The disphenoid is the double orthoscheme face-bonded to its mirror image (a quadruple orthoscheme). Thus all three of these Goursat tetrahedra, and all the polyhedra they generate by reflections, can be dissected into characteristic tetrahedra of the cube.

Isometries of irregular tetrahedra

The isometries of an irregular (unmarked) tetrahedron depend on the geometry of the tetrahedron, with 7 cases possible. In each case a 3-dimensional point group is formed. Two other isometries (C₃, [3]⁺), and (S₄, [2⁺,4⁺]) can exist if the face or edge marking are included. Tetrahedral diagrams are included for each type below, with edges colored by isometric equivalence, and are gray colored for unique edges.

Tetrahedron name				Edge equivalence diagram	Description
Symmetry
Schön.	Cox.	Orb.	Ord.
Regular tetrahedron					Four equilateral triangles It forms the symmetry group Td, isomorphic to the symmetric group, S4. A regular tetrahedron has Coxeter diagram and Schläfli symbol {3,3}.
Td T	[3,3] [3,3]+	*332 332	24 12
Triangular pyramid					An equilateral triangle base and three equal isosceles triangle sides It gives 6 isometries, corresponding to the 6 isometries of the base. As permutations of the vertices, these 6 isometries are the identity 1, (123), (132), (12), (13) and (23), forming the symmetry group C3v, isomorphic to the symmetric group, S3. A triangular pyramid has Schläfli symbol {3}∨( ).
C3v C3	[3] [3]+	*33 33	6 3
Mirrored sphenoid					Two equal scalene triangles with a common base edge This has two pairs of equal edges (1,3), (1,4) and (2,3), (2,4) and otherwise no edges equal. The only two isometries are 1 and the reflection (34), giving the group Cs, also isomorphic to the cyclic group, Z2.
Cs =C1h =C1v	[ ]	*	2
Irregular tetrahedron (No symmetry)					Four unequal triangles Its only isometry is the identity, and the symmetry group is the trivial group. An irregular tetrahedron has Schläfli symbol ( )∨( )∨( )∨( ).
C1	[ ]+	1	1
Disphenoids (Four equal triangles)
Tetragonal disphenoid					Four equal isosceles triangles It has 8 isometries. If edges (1,2) and (3,4) are of different length to the other 4 then the 8 isometries are the identity 1, reflections (12) and (34), and 180° rotations (12)(34), (13)(24), (14)(23) and improper 90° rotations (1234) and (1432) forming the symmetry group D2d. A tetragonal disphenoid has Coxeter diagram and Schläfli symbol s{2,4}.
D2d S4	[2+,4] [2+,4+]	2*2 2×	8 4
Rhombic disphenoid					Four equal scalene triangles It has 4 isometries. The isometries are 1 and the 180° rotations (12)(34), (13)(24), (14)(23). This is the Klein four-group V4 or Z22, present as the point group D2. A rhombic disphenoid has Coxeter diagram and Schläfli symbol sr{2,2}.
D2	[2,2]+	222	4
Generalized disphenoids (2 pairs of equal triangles)
Digonal disphenoid					Two pairs of equal isosceles triangles This gives two opposite edges (1,2) and (3,4) that are perpendicular but different lengths, and then the 4 isometries are 1, reflections (12) and (34) and the 180° rotation (12)(34). The symmetry group is C2v, isomorphic to the Klein four-group V4. A digonal disphenoid has Schläfli symbol { }∨{ }.
C2v C2	[2] [2]+	*22 22	4 2
Phyllic disphenoid					Two pairs of equal scalene or isosceles triangles This has two pairs of equal edges (1,3), (2,4) and (1,4), (2,3) but otherwise no edges equal. The only two isometries are 1 and the rotation (12)(34), giving the group C2 isomorphic to the cyclic group, Z2.
C2	[2]+	22	2

Subdivision and similarity classes

Tetrahedra subdivision is a process used in computational geometry and 3D modeling to divide a tetrahedron into several smaller tetrahedra. This process enhances the complexity and detail of tetrahedral meshes, which is particularly beneficial in numerical simulations, finite element analysis, and computer graphics. One of the commonly used subdivision methods is the Longest Edge Bisection (LEB), which identifies the longest edge of the tetrahedron and bisects it at its midpoint, generating two new, smaller tetrahedra. When this process is repeated multiple times, bisecting all the tetrahedra generated in each previous iteration, the process is called iterative LEB.

A similarity class is the set of tetrahedra with the same geometric shape, regardless of their specific position, orientation, and scale. So, any two tetrahedra belonging to the same similarity class may be transformed to each other by an affine transformation. The outcome of having a limited number of similarity classes in iterative subdivision methods is significant for computational modeling and simulation. It reduces the variability in the shapes and sizes of generated tetrahedra, preventing the formation of highly irregular elements that could compromise simulation results.

The iterative LEB of the regular tetrahedron has been shown to produce only 8 similarity classes. Furthermore, in the case of nearly equilateral tetrahedra where their two longest edges are not connected to each other, and the ratio between their longest and their shortest edge is less than or equal to ${\displaystyle {\sqrt {3/2}}}$, the iterated LEB produces no more than 37 similarity classes.^[23]

General properties

In general, a tetrahedron is a three-dimensional object with four faces, six edges, and four vertices. It can be considered as pyramid whenever one of its faces can be considered as the base. Its skeleton can be generally seen as a graph by Steinitz's theorem, known as tetrahedral graph, one of the Platonic graphs. It is complete graph ${\displaystyle K_{4}}$ because every pair of its vertices has a unique edge. In a plane, this graph can be regarded as a triangle in which three vertices connect to its fourth vertex in the center, known as the universal vertex; hence, the tetrahedral graph is a wheel graph.^[24]

The tetrahedron is one of the polyhedra that does not have space diagonal; the other polyhedra with such a property are Császár polyhedron and Schonhardt polyhedron.^[25] It is also known as 3-simplex, the generalization of a triangle in multi-dimension. It is self-dual, meaning its dual polyhedron is a tetrahedron itself.^[26] Many other properties of tetrahedra are explicitly described in the following sections.

Volume

A simple way to obtain the volume of a tetrahedron is given by the formula for the volume: $${\displaystyle V={\frac {1}{3}}Ah.}$$ where ${\displaystyle A}$ is the base' area and ${\displaystyle h}$ is the height from the base to the apex. This applies to each of the four choices of the base, so the distances from the apices to the opposite faces are inversely proportional to the areas of these faces. Another way is by dissecting a triangular prism into three pieces.^[27]

Algebraic approach

A linear algebra approach is an alternative way by the given vertices in terms of vectors as: $${\displaystyle {\begin{aligned}\mathbf {a} &=(a_{1},a_{2},a_{3}),\\\mathbf {b} &=(b_{1},b_{2},b_{3}),\\\mathbf {c} &=(c_{1},c_{2},c_{3}),\\\mathbf {d} &=(d_{1},d_{2},d_{3}).\end{aligned}}}$$ In terms of a determinant, the volume of a tetrahedron is ${\textstyle {\frac {1}{6}}\det(\mathbf {a} -\mathbf {d} ,\mathbf {b} -\mathbf {d} ,\mathbf {c} -\mathbf {d} )}$, one-sixth of any parallelepiped's volume sharing three converging edges with it.^[28]

Similarly by the given vertices, another approach is by the absolute value of the scalar triple product, representing the absolute values of determinants ${\displaystyle 6\cdot V={\begin{vmatrix}\mathbf {a} &\mathbf {b} &\mathbf {c} \end{vmatrix}}}$. Hence $${\displaystyle 36\cdot V^{2}={\begin{vmatrix}\mathbf {a^{2}} &\mathbf {a} \cdot \mathbf {b} &\mathbf {a} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b^{2}} &\mathbf {b} \cdot \mathbf {c} \\\mathbf {a} \cdot \mathbf {c} &\mathbf {b} \cdot \mathbf {c} &\mathbf {c^{2}} \end{vmatrix}}.}$$

Here ${\displaystyle \mathbf {a} \cdot \mathbf {b} =ab\cos {\gamma }}$, ${\displaystyle \mathbf {b} \cdot \mathbf {c} =bc\cos {\alpha }}$, and ${\displaystyle \mathbf {a} \cdot \mathbf {c} =ac\cos {\beta }.}$ The variables ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$ denotes each norm of a vector ${\displaystyle \mathbf {a} }$, ${\displaystyle \mathbf {b} }$, and ${\displaystyle \mathbf {c} }$ respectively. This gives $${\displaystyle V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}},\,}$$ where the Greek lowercase letters denotes the plane angles occurring in vertex ${\displaystyle \mathbf {d} }$: the angle ${\displaystyle \alpha }$ is an angle between the two edges connecting the vertex ${\displaystyle \mathbf {d} }$ to the vertices ${\displaystyle \mathbf {b} }$ and ${\displaystyle \mathbf {c} }$; the angle ${\displaystyle \beta }$ does so for the vertices ${\displaystyle \mathbf {a} }$ and ${\displaystyle \mathbf {c} }$; while the angle ${\displaystyle \gamma }$ is defined by the position of the vertices ${\displaystyle \mathbf {a} }$ and ${\displaystyle \mathbf {b} }$. Considering that ${\displaystyle \mathbf {d} =0}$, then $${\displaystyle 6\cdot V=\left|\det \left({\begin{matrix}a_{1}&b_{1}&c_{1}&d_{1}\\a_{2}&b_{2}&c_{2}&d_{2}\\a_{3}&b_{3}&c_{3}&d_{3}\\1&1&1&1\end{matrix}}\right)\right|\,.}$$

Given the distances between the vertices of a tetrahedron the volume can be computed using the Cayley–Menger determinant: $${\displaystyle 288\cdot V^{2}={\begin{vmatrix}0&1&1&1&1\\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\\1&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{2}\\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\\1&d_{14}^{2}&d_{24}^{2}&d_{34}^{2}&0\end{vmatrix}}}$$ where the subscripts ${\displaystyle i,j\in \{1,2,3,4\}}$ represent the vertices ${\displaystyle \{\mathbf {a} ,\mathbf {b} ,\mathbf {c} ,\mathbf {d} \}}$, and ${\displaystyle d_{ij}}$ is the pairwise distance between them, the length of the edge connecting the two vertices. A negative value of the determinant means that a tetrahedron cannot be constructed with the given distances. This formula, sometimes called Tartaglia's formula, is essentially due to the painter Piero della Francesca in the 15th century, as a three-dimensional analogue of the 1st century Heron's formula for the area of a triangle.

Other approaches

Let ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$ be the lengths of three edges that meet at a point, and ${\displaystyle x}$, ${\displaystyle y}$, and ${\displaystyle z}$ be those of the opposite edges. The volume of the tetrahedron ${\displaystyle V}$ is:^[29] $${\displaystyle V={\frac {\sqrt {4a^{2}b^{2}c^{2}-a^{2}X^{2}-b^{2}Y^{2}-c^{2}Z^{2}+XYZ}}{12}}}$$ where $${\displaystyle {\begin{aligned}X&=b^{2}+c^{2}-x^{2},\\Y&=a^{2}+c^{2}-y^{2},\\Z&=a^{2}+b^{2}-z^{2}.\end{aligned}}}$$ The above formula uses six lengths of edges, and the following formula uses three lengths of edges and three angles.^[29] $${\displaystyle V={\frac {abc}{6}}{\sqrt {1+2\cos {\alpha }\cos {\beta }\cos {\gamma }-\cos ^{2}{\alpha }-\cos ^{2}{\beta }-\cos ^{2}{\gamma }}}}$$

Six edge-lengths of Tetrahedron

The volume of a tetrahedron can be ascertained by using the Heron formula. Suppose ${\displaystyle U}$, ${\displaystyle V}$, ${\displaystyle W}$, ${\displaystyle u}$. ${\displaystyle v}$, and ${\displaystyle w}$ are the lengths of the tetrahedron's edges as in the following image. Here, the first three form a triangle, with ${\displaystyle u}$ opposite ${\displaystyle U}$, ${\displaystyle v}$ opposite ${\displaystyle V}$, and ${\displaystyle w}$ opposite ${\displaystyle W}$. Then, $${\displaystyle V={\frac {\sqrt {\,(-p+q+r+s)\,(p-q+r+s)\,(p+q-r+s)\,(p+q+r-s)}}{192\,u\,v\,w}}}$$ where $${\displaystyle {\begin{aligned}p={\sqrt {xYZ}},&\quad q={\sqrt {yZX}},\\r={\sqrt {zXY}},&\quad s={\sqrt {xyz}},\end{aligned}}}$$ and $${\displaystyle {\begin{aligned}X=(w-U+v)(U+v+w),&\quad x=(U-v+w)(v-w+U),\\Y=(u-V+w)(V+w+u),&\quad y=(V-w+u)(w-u+V),\\Z=(v-W+u)(W+u+v),&\quad z=(W-u+v)\,(u-v+W).\end{aligned}}}$$

Any plane containing a bimedian (connector of opposite edges' midpoints) of a tetrahedron bisects the volume of the tetrahedron.^[30]

For tetrahedra in hyperbolic space or in three-dimensional elliptic geometry, the dihedral angles of the tetrahedron determine its shape and hence its volume. In these cases, the volume is given by the Murakami–Yano formula, after Jun Murakami and Masakazu Yano.^[31] However, in Euclidean space, scaling a tetrahedron changes its volume but not its dihedral angles, so no such formula can exist.

Any two opposite edges of a tetrahedron lie on two skew lines, and the distance between the edges is defined as the distance between the two skew lines. Let ${\displaystyle d}$ be the distance between the skew lines formed by opposite edges ${\displaystyle a}$ and ${\displaystyle \mathbf {b} -\mathbf {c} }$ as calculated here. Then another formula for the volume of a tetrahedron ${\displaystyle V}$ is given by $${\displaystyle V={\frac {d|(\mathbf {a} \times \mathbf {(b-c)} )|}{6}}.}$$

Analogous to a triangle

The tetrahedron has many properties analogous to those of a triangle, including an insphere, circumsphere, medial tetrahedron, and exspheres. It has respective centers such as incenter, circumcenter, excenters, Spieker center and points such as a centroid. However, there is generally no orthocenter in the sense of intersecting altitudes.^[32]

Gaspard Monge found a center that exists in every tetrahedron, now known as the Monge point: the point where the six midplanes of a tetrahedron intersect. A midplane is defined as a plane that is orthogonal to an edge joining any two vertices that also contains the centroid of an opposite edge formed by joining the other two vertices.^[33] An orthogonal line dropped from the Monge point to any face meets that face at the midpoint of the line segment between that face's orthocenter and the foot of the altitude dropped from the opposite vertex. If the tetrahedron's altitudes do intersect, then the Monge point and the orthocenter coincide to give the class of orthocentric tetrahedron.

A line segment joining a vertex of a tetrahedron with the centroid of the opposite face is called a median and a line segment joining the midpoints of two opposite edges is called a bimedian of the tetrahedron. Hence, a tetrahedron has four medians and three bimedians. These seven line segments are all concurrent at a point called the centroid of the tetrahedron.^[34] In addition, the four medians are divided in a 3:1 ratio by the centroid.^[35] The centroid of a tetrahedron is the midpoint between its Monge point and circumcenter. These points define the Euler line of the tetrahedron that is analogous to the Euler line of a triangle.

The nine-point circle of the general triangle has an analogue in the circumsphere of a tetrahedron's medial tetrahedron. It is the twelve-point sphere and besides the centroids of the four faces of the reference tetrahedron, it passes through four substitute Euler points, one third of the way from the Monge point toward each of the four vertices. Finally, it passes through the four base points of orthogonal lines dropped from each Euler point to the face not containing the vertex that generated the Euler point.^[36]

The center ${\displaystyle T}$ of the twelve-point sphere also lies on the Euler line. Unlike its triangular counterpart, this center lies one-third of the way from the Monge point ${\displaystyle M}$ towards the circumcenter. Additionally, an orthogonal line through ${\displaystyle T}$ to a chosen face is coplanar with two other orthogonal lines to the same face. The first is an orthogonal line passing through the corresponding Euler point to the chosen face. The second is an orthogonal line passing through the centroid of the chosen face. This orthogonal line through the twelve-point center lies midway between the Euler point orthogonal line and the centroidal orthogonal line. Furthermore, for any face, the twelve-point center lies at the midpoint of the corresponding Euler point and the orthocenter for that face.

The radius of the twelve-point sphere is one-third of the circumradius of the reference tetrahedron.

There is a relation among the angles made by the faces of a general tetrahedron given by^[37]

${\displaystyle {\begin{vmatrix}-1&\cos {(\alpha _{12})}&\cos {(\alpha _{13})}&\cos {(\alpha _{14})}\\\cos {(\alpha _{12})}&-1&\cos {(\alpha _{23})}&\cos {(\alpha _{24})}\\\cos {(\alpha _{13})}&\cos {(\alpha _{23})}&-1&\cos {(\alpha _{34})}\\\cos {(\alpha _{14})}&\cos {(\alpha _{24})}&\cos {(\alpha _{34})}&-1\\\end{vmatrix}}=0\,}$

where ${\displaystyle \alpha _{ij}}$ is the angle between the faces ${\displaystyle i}$ and ${\displaystyle j}$.

The geometric median of the vertex position coordinates of a tetrahedron and its isogonic center are associated, under circumstances analogous to those observed for a triangle. Lorenz Lindelöf found that, corresponding to any given tetrahedron is a point now known as an isogonic center, ${\displaystyle O}$, at which the solid angles subtended by the faces are equal, having a common value of ${\displaystyle \pi }$ sr, and at which the angles subtended by opposite edges are equal.^[38] A solid angle of ${\displaystyle \pi }$ sr is one quarter of that subtended by all of space. When all the solid angles at the vertices of a tetrahedron are smaller than ${\displaystyle \pi }$ sr, ${\displaystyle O}$ lies inside the tetrahedron. Because the sum of distances from ${\displaystyle O}$ to the vertices is a minimum, ${\displaystyle O}$ coincides with the geometric median ${\displaystyle M}$ of the vertices. If the solid angle at one of the vertices ${\displaystyle v}$ measures exactly ${\displaystyle \pi }$ sr, then ${\displaystyle O}$ and ${\displaystyle M}$ coincide with ${\displaystyle v}$. However, if a tetrahedron has a vertex ${\displaystyle v}$ with solid angle greater than ${\displaystyle \pi }$ sr, ${\displaystyle M}$ still corresponds to ${\displaystyle v}$, but ${\displaystyle O}$ lies outside the tetrahedron.

Trigonometry and the space of all shapes

Main article: Trigonometry of a tetrahedron

Illustration of the law of sines for tetrahedra

A corollary of the usual law of sines is that in a tetrahedron with vertices ${\displaystyle O}$, ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$, is given by $${\displaystyle \sin \angle OAB\cdot \sin \angle OBC\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \angle OCB\cdot \sin \angle OBA.}$$ One may view the two sides of this identity as corresponding to clockwise and counterclockwise orientations of the surface. Putting any of the four vertices in the role of ${\displaystyle O}$ yields four such identities, but at most three of them are independent. If the "clockwise" sides of three of them are multiplied and the product is inferred to be equal to the product of the "counterclockwise" sides of the same three identities. Hence, common factors are cancelled from both sides, and the result is the fourth identity.

Three angles are the angles of some triangle if and only if their sum is 180° (π radians). What condition on 12 angles is necessary and sufficient for them to be the 12 angles of some tetrahedron? The sum of the angles of any side of the tetrahedron must be 180°. Since there are four such triangles, there are four such constraints on sums of angles, and the number of degrees of freedom is thereby reduced from 12 to 8. The four relations given by this sine law further reduce the number of degrees of freedom, from 8 down to not 4 but 5, since the fourth constraint is not independent of the first three. Thus, the space of all shapes of tetrahedra is 5-dimensional.^[39]

Let ${\displaystyle P_{1}}$, ${\displaystyle P_{2}}$, ${\displaystyle P_{3}}$, ${\displaystyle P_{4}}$ be the points of a tetrahedron. Let ${\displaystyle \Delta _{i}}$ be the area of the face opposite vertex ${\displaystyle P_{i}}$ and let ${\displaystyle \theta _{ij}}$ be the dihedral angle between the two faces of the tetrahedron adjacent to the edge ${\displaystyle P_{i}P_{j}}$. The law of cosines for a tetrahedron, which relates the areas of the faces of the tetrahedron to the dihedral angles about a vertex, is given by the following relation:^[40] $${\displaystyle \Delta _{i}^{2}=\Delta _{j}^{2}+\Delta _{k}^{2}+\Delta _{l}^{2}-2(\Delta _{j}\Delta _{k}\cos \theta _{il}+\Delta _{j}\Delta _{l}\cos \theta _{ik}+\Delta _{k}\Delta _{l}\cos \theta _{ij})}$$

Interior point

Let ${\displaystyle P}$ be any interior point of a tetrahedron of volume ${\displaystyle V}$ for which the vertices are ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$, and ${\displaystyle D}$, and for which the areas of the opposite faces are ${\displaystyle F_{a}}$, ${\displaystyle F_{b}}$, ${\displaystyle F_{c}}$, and ${\displaystyle F_{d}}$. Then,^[41] $${\displaystyle PA\cdot F_{\mathrm {a} }+PB\cdot F_{\mathrm {b} }+PC\cdot F_{\mathrm {c} }+PD\cdot F_{\mathrm {d} }\geq 9V.}$$

For vertices ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$, and ${\displaystyle D}$, interior point ${\displaystyle P}$, and feet ${\displaystyle J}$, ${\displaystyle K}$, ${\displaystyle L}$, and ${\displaystyle M}$ of the perpendiculars from ${\displaystyle P}$ to the faces, and suppose the faces have equal areas, then:^[42] $${\displaystyle PA+PB+PC+PD\geq 3(PJ+PK+PL+PM).}$$

Inradius

Denoting the inradius of a tetrahedron as ${\displaystyle r}$ and the inradii of its triangular faces as ${\displaystyle r_{1}}$ for ${\displaystyle i=1,2,3,4}$, then:^[43] $${\displaystyle {\frac {1}{r_{1}^{2}}}+{\frac {1}{r_{2}^{2}}}+{\frac {1}{r_{3}^{2}}}+{\frac {1}{r_{4}^{2}}}\leq {\frac {2}{r^{2}}},}$$ with equality if and only if the tetrahedron is regular.

If ${\displaystyle A_{1}}$, ${\displaystyle A_{2}}$, ${\displaystyle A_{3}}$ and ${\displaystyle A_{4}}$ denote the area of each faces, the value of ${\displaystyle r}$ is given by $${\displaystyle r={\frac {3V}{A_{1}+A_{2}+A_{3}+A_{4}}}.}$$

This formula is obtained from dividing the tetrahedron into four tetrahedra whose points are the three points of one of the original faces and the incenter. Since the four subtetrahedra fill the volume, then: $${\displaystyle V={\frac {1}{3}}A_{1}r+{\frac {1}{3}}A_{2}r+{\frac {1}{3}}A_{3}r+{\frac {1}{3}}A_{4}r.}$$

Circumradius

Denote the circumradius of a tetrahedron as R. Let a, b, c be the lengths of the three edges that meet at a vertex, and A, B, C the length of the opposite edges. Let V be the volume of the tetrahedron. Then^[44][45]

${\displaystyle R={\frac {\sqrt {(aA+bB+cC)(aA+bB-cC)(aA-bB+cC)(-aA+bB+cC)}}{24V}}.}$

Circumcenter

The circumcenter of a tetrahedron can be found as intersection of three bisector planes. A bisector plane is defined as the plane centered on, and orthogonal to an edge of the tetrahedron. With this definition, the circumcenter C of a tetrahedron with vertices x₀,x₁,x₂,x₃ can be formulated as matrix-vector product:^[46]

${\displaystyle {\begin{aligned}C&=A^{-1}B&{\text{where}}&\ &A=\left({\begin{matrix}\left[x_{1}-x_{0}\right]^{T}\\\left[x_{2}-x_{0}\right]^{T}\\\left[x_{3}-x_{0}\right]^{T}\end{matrix}}\right)&\ &{\text{and}}&\ &B={\frac {1}{2}}\left({\begin{matrix}\|x_{1}\|^{2}-\|x_{0}\|^{2}\\\|x_{2}\|^{2}-\|x_{0}\|^{2}\\\|x_{3}\|^{2}-\|x_{0}\|^{2}\end{matrix}}\right)\\\end{aligned}}}$

In contrast to the centroid, the circumcenter may not always lay on the inside of a tetrahedron. Analogously to an obtuse triangle, the circumcenter is outside of the object for an obtuse tetrahedron.

Integer tetrahedra

Main article: Heronian tetrahedron

There exist tetrahedra having integer-valued edge lengths, face areas and volume. These are called Heronian tetrahedra. One example has one edge of 896, the opposite edge of 990 and the other four edges of 1073; two faces are isosceles triangles with areas of 436800 and the other two are isosceles with areas of 47120, while the volume is 124185600.^[47]

A tetrahedron can have integer volume and consecutive integers as edges, an example being the one with edges 6, 7, 8, 9, 10, and 11 and volume 48.^[48]

Applications

A four-sided die and pyramorphix

The Royal Game of Ur, dating from 2600 BC, was played with a set of tetrahedral dice. Especially in roleplaying, this solid is known as a 4-sided die, one of the more common polyhedral dice, with the number rolled appearing around the bottom or on the top vertex. Some Rubik's Cube-like puzzles are tetrahedral, such as the Pyraminx and Pyramorphix.

Stanley Kubrick originally intended the monolith in 2001: A Space Odyssey to be a tetrahedron, according to Marvin Minsky, a cognitive scientist and expert on artificial intelligence who advised Kubrick on the HAL 9000 computer and other aspects of the movie. Kubrick scrapped the idea of using the tetrahedron as a visitor who saw footage of it did not recognize what it was and he did not want anything in the movie regular people did not understand.^[49] The tetrahedron with regular faces is a solution to an old puzzle asking to form four equilateral triangles using six unbroken matchsticks. The solution places the matchsticks along the edges of a tetrahedron.^[50]

An irregular volume in space can be approximated by an irregular triangulated surface, and irregular tetrahedral volume elements.

A caltrop

Several applications of tetrahedra in related fields with engineering are the following:

• In numerical analysis, complicated three-dimensional shapes are commonly broken down into, or approximated by, a polygonal mesh of irregular tetrahedra in the process of setting up the equations for finite element analysis especially in the numerical solution of partial differential equations.^[51] These methods have wide applications in practical applications in computational fluid dynamics,^[52] aerodynamics, electromagnetic fields, civil engineering, chemical engineering, naval architecture and engineering, and related fields.
• The tetrahedron has inherently rigid.^[53] For this reason, it is often used to stiffen frame structures such as spaceframes.
• The tetrahedron is used in caltrops to provide an area denial weapon. This is due to their nature of having a sharp corner that always points upwards.^[54] Large steel tetrahedra have been used as anti-tank measures,^[55] or concrete tetrahedra as tetrapods to break down waves at coastlines.^[56]
• At some airfields, a large frame in the shape of a tetrahedron with two sides covered with a thin material is mounted on a rotating pivot and always points into the wind. It is built big enough to be seen from the air and is sometimes illuminated. Its purpose is to serve as a reference to pilots, indicating wind direction.^[57]

The tetrahedron can be described as tetrahedral molecular geometry in stereochemistry.^[58] This chemical structure can be found in water H
₂O and methane (CH
₄).^[59] The tetrahedron shape is seen in nature in covalently bonded molecules. All sp³-hybridized atoms are surrounded by atoms (or lone electron pairs) at the four corners of a tetrahedron. For this reason, one of the leading journals in organic chemistry is called Tetrahedron. For a perfect tetrahedron, the central angle between any two vertices is arccos(−⁠1/3⁠), or approximately 109.47°.^[60]

Quaternary phase diagrams of mixtures of chemical substances are represented graphically as tetrahedra. However, quaternary phase diagrams in communication engineering are represented graphically on a two-dimensional plane.

The vertices of a regular tetrahedron applies as the minimum solution known for ${\displaystyle n=4}$ in both Thomson problem (concerning the minimum-energy configuration of ${\displaystyle n}$ charged particles on a sphere) and for the Tammes problem (of constructing a spherical code maximizing the smallest distance among the points).^[61]

If six equal resistors are soldered together to form a tetrahedron, then the resistance measured between any two vertices is half that of one resistor.^[62] Since silicon is the most common semiconductor used in solid-state electronics, and silicon has a valence of four, the tetrahedral shape of the four chemical bonds in silicon is a strong influence on how crystals of silicon form and what shapes they assume.

Tetrahedra are used in color space conversion algorithms specifically for cases in which the luminance axis diagonally segments the color space (e.g. RGB, CMY).^[63]

The tetrahedral hypothesis, originally published by William Lowthian Green, explains the formation of the Earth with the shape of a tetrahedron.^[64] It was popular through the early 20th century.^[65][66]

Related topics

Regular tetrahedra cannot tessellate space by themselves, although this result seems likely enough that Aristotle claimed it was possible. However, two regular tetrahedra can be combined with an octahedron, giving a rhombohedron that can tile space as the tetrahedral-octahedral honeycomb. On the other hand, several irregular tetrahedra are known, of which copies can tile space, for instance, the characteristic orthoscheme of the cube and the disphenoid of the disphenoid tetrahedral honeycomb. The complete list remains an open problem.^[67]

If one relaxes the requirement that the tetrahedra be all the same shape, one can tile space using only tetrahedra in many different ways. For example, one can divide an octahedron into four identical tetrahedra and combine them again with two regular ones. (As a side-note: these two kinds of tetrahedron have the same volume.)

The tetrahedron is unique among the uniform polyhedra in possessing no parallel faces.

See also

• Boerdijk–Coxeter helix
• Möbius configuration
• Caltrop
• Demihypercube and simplex – n-dimensional analogues
• Synergetics (Fuller)
• Tetrahedral kite
• Tetrahedral number
• Tetrahedroid
• Tetrahedron packing
• Triangular dipyramid – constructed by joining two tetrahedra along one face
• Trirectangular tetrahedron
• Orthoscheme

Notes

1. (Coxeter 1973) uses the greek letter 𝝓 (phi) to represent one of the three characteristic angles 𝟀, 𝝓, 𝟁 of a regular polytope. Because 𝝓 is commonly used to represent the golden ratio constant ≈ 1.618, for which Coxeter uses 𝝉 (tau), we reverse Coxeter's conventions, and use 𝝉 to represent the characteristic angle.