Octahedron

Not to be confused with Octahedron (album).

In geometry, an octahedron (pl.: octahedra or octahedrons) is a polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. Many types of irregular octahedra also exist, including both convex and non-convex shapes.

A regular octahedron is the three-dimensional case of the more general concept of a cross-polytope.

Regular octahedron

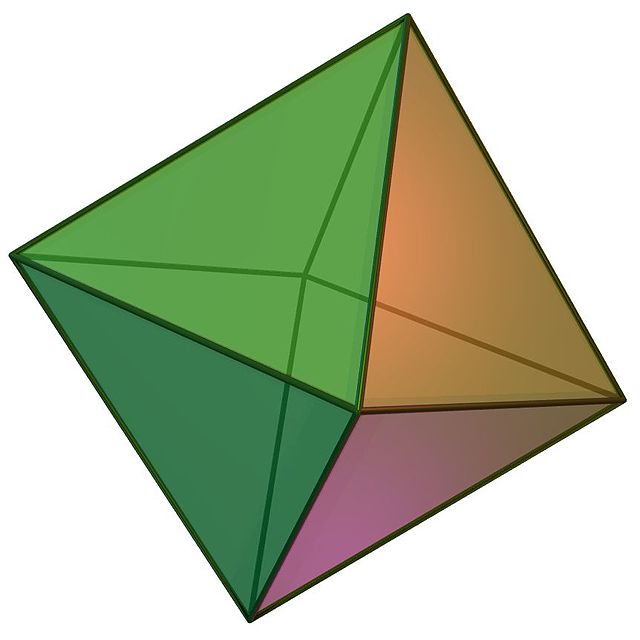
The regular octahedron and its dual polyhedron, the cube.

A regular octahedron is an octahedron that is a regular polyhedron. All the faces of a regular octahedron are equilateral triangles of the same size, and exactly four triangles meet at each vertex. A regular octahedron is convex, meaning that for any two points within it, the line segment connecting them lies entirely within it.

It is one of the eight convex deltahedra because all of the faces are equilateral triangles.^[1] It is a composite polyhedron made by attaching two equilateral square pyramids.^[2][3] Its dual polyhedron is the cube, and they have the same three-dimensional symmetry groups, the octahedral symmetry ${\displaystyle \mathrm {O} _{\mathrm {h} }}$.^[3]

As a Platonic solid

Sketch of a regular octahedron by Johannes Kepler

Kepler's Platonic solid model of the Solar System

The regular octahedron is one of the Platonic solids, a set of polyhedrons whose faces are congruent regular polygons and the same number of faces meet at each vertex.^[4] This ancient set of polyhedrons was named after Plato who, in his Timaeus dialogue, related these solids to nature. One of them, the regular octahedron, represented the classical element of wind.^[5]

Following its attribution with nature by Plato, Johannes Kepler in his Harmonices Mundi sketched each of the Platonic solids.^[5] In his Mysterium Cosmographicum, Kepler also proposed the Solar System by using the Platonic solids setting into another one and separating them with six spheres resembling the six planets. The ordered solids started from the innermost to the outermost: regular octahedron, regular icosahedron, regular dodecahedron, regular tetrahedron, and cube.^[6]

Like its dual, the regular octahedron has three properties: any two faces, two vertices, and two edges are transformed by rotation and reflection under the symmetry orbit, such that the appearance remains unchanged; these are isohedral, isogonal, and isotoxal respectively. Hence, it is considered a regular polyhedron. Four triangles surround each vertex, so the regular octahedron is ${\displaystyle 3.3.3.3}$ by vertex configuration or ${\displaystyle \{3,4\}}$ by Schläfli symbol.^[7]

As a square bipyramid

Square bipyramid

Many octahedra of interest are square bipyramids.^[8] A square bipyramid is a bipyramid constructed by attaching two square pyramids base-to-base. These pyramids cover their square bases, so the resulting polyhedron has eight triangular faces.^[1]

A square bipyramid is said to be right if the square pyramids are symmetrically regular and both of their apices are on the line passing through the base's center; otherwise, it is oblique.^[9] The resulting bipyramid has three-dimensional point group of dihedral group ${\displaystyle D_{4\mathrm {h} }}$ of sixteen: the appearance is symmetrical by rotating around the axis of symmetry that passing through apices and base's center vertically, and it has mirror symmetry relative to any bisector of the base; it is also symmetrical by reflecting it across a horizontal plane.^[10] Therefore, this square bipyramid is face-transitive or isohedral.^[11]

If the edges of a square bipyramid are all equal in length, then that square bipyramid is a regular octahedron.

Metric properties and Cartesian coordinates

3D model of regular octahedron

The surface area ${\displaystyle A}$ of a regular octahedron can be ascertained by summing all of its eight equilateral triangles, whereas its volume ${\displaystyle V}$ is twice the volume of a square pyramid; if the edge length is ${\displaystyle a}$,^[12] $${\displaystyle {\begin{aligned}A&=2{\sqrt {3}}a^{2}&\approx 3.464a^{2},\\V&={\frac {1}{3}}{\sqrt {2}}a^{3}&\approx 0.471a^{3}.\end{aligned}}}$$ The radius of a circumscribed sphere ${\displaystyle r_{u}}$ (one that touches the octahedron at all vertices), the radius of an inscribed sphere ${\displaystyle r_{i}}$ (one that tangent to each of the octahedron's faces), and the radius of a midsphere ${\displaystyle r_{m}}$ (one that touches the middle of each edge), are:^[13] $${\displaystyle r_{u}={\frac {\sqrt {2}}{2}}a\approx 0.707a,\qquad r_{i}={\frac {\sqrt {6}}{6}}a\approx 0.408a,\qquad r_{m}={\frac {1}{2}}a=0.5a.}$$

The dihedral angle of a regular octahedron between two adjacent triangular faces is 109.47°. This can be obtained from the dihedral angle of an equilateral square pyramid: its dihedral angle between two adjacent triangular faces is the dihedral angle of an equilateral square pyramid between two adjacent triangular faces, and its dihedral angle between two adjacent triangular faces on the edge in which two equilateral square pyramids are attached is twice the dihedral angle of an equilateral square pyramid between its triangular face and its square base.^[14]

An octahedron with edge length ${\displaystyle {\sqrt {2}}}$ can be placed with its center at the origin and its vertices on the coordinate axes; the Cartesian coordinates of the vertices are:^[15] $${\displaystyle (\pm 1,0,0),\qquad (0,\pm 1,0),\qquad (0,0,\pm 1).}$$

Graph

The graph of a regular octahedron

The skeleton of a regular octahedron can be represented as a graph according to Steinitz's theorem, provided the graph is planar—its edges of a graph are connected to every vertex without crossing other edges—and 3-connected graph—its edges remain connected whenever two of more three vertices of a graph are removed.^[16][17] Its graph called the octahedral graph, a Platonic graph.^[4]

The octahedral graph can be considered as complete tripartite graph ${\displaystyle K_{2,2,2}}$, a graph partitioned into three independent sets each consisting of two opposite vertices.^[18] More generally, it is a Turán graph ${\displaystyle T_{6,3}}$.

The octahedral graph is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the pentagonal dipyramid, the snub disphenoid, and an irregular polyhedron with 12 vertices and 20 triangular faces.^[19]

Related figures

The octahedron represents the central intersection of two tetrahedra

The interior of the compound of two dual tetrahedra is an octahedron, and this compound—called the stella octangula—is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and icosidodecahedron relate to the other Platonic solids.

One can also divide the edges of an octahedron in the ratio of the golden mean to define the vertices of a regular icosahedron. This is done by first placing vectors along the octahedron's edges such that each face is bounded by a cycle, then similarly partitioning each edge into the golden mean along the direction of its vector. Five octahedra define any given icosahedron in this fashion, and together they define a regular compound. A regular icosahedron produced this way is called a snub octahedron.^[20]

The regular octahedron can be considered as the antiprism, a prism like polyhedron in which lateral faces are replaced by alternating equilateral triangles. It is also called trigonal antiprism.^[21] Therefore, it has the property of quasiregular, a polyhedron in which two different polygonal faces are alternating and meet at a vertex.^[22]

Octahedra and tetrahedra can be alternated to form a vertex, edge, and face-uniform tessellation of space. This and the regular tessellation of cubes are the only such uniform honeycombs in 3-dimensional space.

The uniform tetrahemihexahedron is a tetrahedral symmetry faceting of the regular octahedron, sharing edge and vertex arrangement. It has four of the triangular faces, and 3 central squares.

A regular octahedron is a 3-ball in the Manhattan (ℓ₁) metric.

Characteristic orthoscheme

Like all regular convex polytopes, the octahedron can be dissected into an integral number of disjoint orthoschemes, all of the same shape characteristic of the polytope. A polytope's characteristic orthoscheme is a fundamental property because the polytope is generated by reflections in the facets of its orthoscheme. The orthoscheme occurs in two chiral forms which are mirror images of each other. The characteristic orthoscheme of a regular polyhedron is a quadrirectangular irregular tetrahedron.

The faces of the octahedron's characteristic tetrahedron lie in the octahedron's mirror planes of symmetry. The octahedron is unique among the Platonic solids in having an even number of faces meeting at each vertex. Consequently, it is the only member of that group to possess, among its mirror planes, some that do not pass through any of its faces. The octahedron's symmetry group is denoted B₃. The octahedron and its dual polytope, the cube, have the same symmetry group but different characteristic tetrahedra.

The characteristic tetrahedron of the regular octahedron can be found by a canonical dissection^[23] of the regular octahedron which subdivides it into 48 of these characteristic orthoschemes surrounding the octahedron's center. Three left-handed orthoschemes and three right-handed orthoschemes meet in each of the octahedron's eight faces, the six orthoschemes collectively forming a trirectangular tetrahedron: a triangular pyramid with the octahedron face as its equilateral base, and its cube-cornered apex at the center of the octahedron.^[24]

Characteristics of the regular octahedron[25]
	edge	arc		dihedral
𝒍	${\displaystyle 2}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$	109°28′	${\displaystyle \pi -2\psi }$
𝟀	${\displaystyle {\sqrt {\tfrac {4}{3}}}\approx 1.155}$	54°44′8″	${\displaystyle {\tfrac {\pi }{2}}-\kappa }$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
𝝉[a]	${\displaystyle 1}$	45°	${\displaystyle {\tfrac {\pi }{4}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
𝟁	${\displaystyle {\sqrt {\tfrac {1}{3}}}\approx 0.577}$	35°15′52″	${\displaystyle \kappa }$	45°	${\displaystyle {\tfrac {\pi }{4}}}$
${\displaystyle _{0}R/l}$	${\displaystyle {\sqrt {2}}\approx 1.414}$
${\displaystyle _{1}R/l}$	${\displaystyle 1}$
${\displaystyle _{2}R/l}$	${\displaystyle {\sqrt {\tfrac {2}{3}}}\approx 0.816}$
${\displaystyle \kappa }$		35°15′52″	${\displaystyle {\tfrac {{\text{arc sec }}3}{2}}}$

If the octahedron has edge length 𝒍 = 2, its characteristic tetrahedron's six edges have lengths ${\displaystyle {\sqrt {\tfrac {4}{3}}}}$, ${\displaystyle 1}$, ${\displaystyle {\sqrt {\tfrac {1}{3}}}}$ around its exterior right-triangle face (the edges opposite the characteristic angles 𝟀, 𝝉, 𝟁),^[a] plus ${\displaystyle {\sqrt {2}}}$, ${\displaystyle 1}$, ${\displaystyle {\sqrt {\tfrac {2}{3}}}}$ (edges that are the characteristic radii of the octahedron). The 3-edge path along orthogonal edges of the orthoscheme is ${\displaystyle 1}$, ${\displaystyle {\sqrt {\tfrac {1}{3}}}}$, ${\displaystyle {\sqrt {\tfrac {2}{3}}}}$, first from an octahedron vertex to an octahedron edge center, then turning 90° to an octahedron face center, then turning 90° to the octahedron center. The orthoscheme has four dissimilar right triangle faces. The exterior face is a 90-60-30 triangle which is one-sixth of an octahedron face. The three faces interior to the octahedron are: a 45-90-45 triangle with edges ${\displaystyle 1}$, ${\displaystyle {\sqrt {2}}}$, ${\displaystyle 1}$, a right triangle with edges ${\displaystyle {\sqrt {\tfrac {1}{3}}}}$, ${\displaystyle 1}$, ${\displaystyle {\sqrt {\tfrac {2}{3}}}}$, and a right triangle with edges ${\displaystyle {\sqrt {\tfrac {4}{3}}}}$, ${\displaystyle {\sqrt {2}}}$, ${\displaystyle {\sqrt {\tfrac {2}{3}}}}$.

Uniform colorings and symmetry

There are 3 uniform colorings of the octahedron, named by the triangular face colors going around each vertex: 1212, 1112, 1111.

The octahedron's symmetry group is O_h, of order 48, the three dimensional hyperoctahedral group. This group's subgroups include D_3d (order 12), the symmetry group of a triangular antiprism; D_4h (order 16), the symmetry group of a square bipyramid; and T_d (order 24), the symmetry group of a rectified tetrahedron. These symmetries can be emphasized by different colorings of the faces.

Name	Octahedron	Rectified tetrahedron (Tetratetrahedron)	Triangular antiprism	Square bipyramid	Rhombic fusil
Image (Face coloring)	(1111)	(1212)	(1112)	(1111)	(1111)
Coxeter diagram		=
Schläfli symbol	{3,4}	r{3,3}	s{2,6} sr{2,3}	ft{2,4} { } + {4}	ftr{2,2} { } + { } + { }
Wythoff symbol	4 | 3 2	2 | 4 3	2 | 6 2 | 2 3 2
Symmetry	Oh, [4,3], (*432)	Td, [3,3], (*332)	D3d, [2+,6], (2*3) D3, [2,3]+, (322)	D4h, [2,4], (*422)	D2h, [2,2], (*222)
Order	48	24	12 6	16	8

Other types of octahedra

A regular faced convex polyhedron, the gyrobifastigium.

An octahedron can be any polyhedron with eight faces. In a previous example, the regular octahedron has 6 vertices and 12 edges, the minimum for an octahedron; irregular octahedra may have as many as 12 vertices and 18 edges.^[26] There are 257 topologically distinct convex octahedra, excluding mirror images. More specifically there are 2, 11, 42, 74, 76, 38, 14 for octahedra with 6 to 12 vertices respectively.^[27][28] (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.) Some of the polyhedrons do have eight faces aside from being square bipyramids in the following:

• Hexagonal prism: Two faces are parallel regular hexagons; six squares link corresponding pairs of hexagon edges.
• Heptagonal pyramid: One face is a heptagon (usually regular), and the remaining seven faces are triangles (usually isosceles). All triangular faces can't be equilateral.
• Truncated tetrahedron: The four faces from the tetrahedron are truncated to become regular hexagons, and there are four more equilateral triangle faces where each tetrahedron vertex was truncated.
• Tetragonal trapezohedron: The eight faces are congruent kites.
• Gyrobifastigium: Two uniform triangular prisms glued over one of their square sides so that no triangle shares an edge with another triangle (Johnson solid 26).
• Truncated triangular trapezohedron, also called Dürer's solid: Obtained by truncating two opposite corners of a cube or rhombohedron, this has six pentagon faces and two triangle faces.^[29]
• Octagonal hosohedron: degenerate in Euclidean space, but can be realized spherically.

Bricard octahedron with an antiparallelogram as its equator. The axis of symmetry passes through the plane of the antiparallelogram.

The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it:

• Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral.
• Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all three quadrilaterals are planar squares.
• Schönhardt polyhedron, a non-convex polyhedron that cannot be partitioned into tetrahedra without introducing new vertices.
• Bricard octahedron, a non-convex self-crossing flexible polyhedron

Octahedra in the physical world

Octahedra in nature

Fluorite octahedron.

• Natural crystals of diamond, alum or fluorite are commonly octahedral, as the space-filling tetrahedral-octahedral honeycomb.
• The plates of kamacite alloy in octahedrite meteorites are arranged paralleling the eight faces of an octahedron.
• Many metal ions coordinate six ligands in an octahedral or distorted octahedral configuration.
• Widmanstätten patterns in nickel-iron crystals

Octahedra in art and culture

Two identically formed Rubik's Snakes can approximate an octahedron.

• Especially in roleplaying games, this solid is known as a "d8", one of the more common polyhedral dice.
• If each edge of an octahedron is replaced by a one-ohm resistor, the resistance between opposite vertices is ⁠1/2⁠ ohm, and that between adjacent vertices ⁠5/12⁠ ohm.^[30]
• Six musical notes can be arranged on the vertices of an octahedron in such a way that each edge represents a consonant dyad and each face represents a consonant triad; see hexany.

Tetrahedral octet truss

A space frame of alternating tetrahedra and half-octahedra derived from the Tetrahedral-octahedral honeycomb was invented by Buckminster Fuller in the 1950s. It is commonly regarded as the strongest building structure for resisting cantilever stresses.

Related polyhedra

A regular octahedron can be augmented into a tetrahedron by adding 4 tetrahedra on alternated faces. Adding tetrahedra to all 8 faces creates the stellated octahedron.

tetrahedron	stellated octahedron

The octahedron is one of a family of uniform polyhedra related to the cube.

Uniform octahedral polyhedra
Symmetry: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= or	= or	=
Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

It is also one of the simplest examples of a hypersimplex, a polytope formed by certain intersections of a hypercube with a hyperplane.

The octahedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane.

*n32 symmetry mutation of regular tilings: {3,n} v t e
Spherical				Euclid.	Compact hyper.		Paraco.	Noncompact hyperbolic
3.3	33	34	35	36	37	38	3∞	312i	39i	36i	33i

Tetratetrahedron

The regular octahedron can also be considered a rectified tetrahedron – and can be called a tetratetrahedron. This can be shown by a 2-color face model. With this coloring, the octahedron has tetrahedral symmetry.

Compare this truncation sequence between a tetrahedron and its dual:

Family of uniform tetrahedral polyhedra
Symmetry: [3,3], (*332)							[3,3]+, (332)
{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duals to uniform polyhedra
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

The above shapes may also be realized as slices orthogonal to the long diagonal of a tesseract. If this diagonal is oriented vertically with a height of 1, then the first five slices above occur at heights r, ⁠3/8⁠, ⁠1/2⁠, ⁠5/8⁠, and s, where r is any number in the range 0 < r ≤ ⁠1/4⁠, and s is any number in the range ⁠3/4⁠ ≤ s < 1.

The octahedron as a tetratetrahedron exists in a sequence of symmetries of quasiregular polyhedra and tilings with vertex configurations (3.n)², progressing from tilings of the sphere to the Euclidean plane and into the hyperbolic plane. With orbifold notation symmetry of *n32 all of these tilings are Wythoff constructions within a fundamental domain of symmetry, with generator points at the right angle corner of the domain.^[31][32]

*n32 orbifold symmetries of quasiregular tilings: (3.n)2
Construction	Spherical			Euclidean	Hyperbolic
	*332	*432	*532	*632	*732	*832...	*∞32
Quasiregular figures
Vertex	(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2

Trigonal antiprism

As a trigonal antiprism, the octahedron is related to the hexagonal dihedral symmetry family.

Uniform hexagonal dihedral spherical polyhedra
Symmetry: [6,2], (*622)							[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
Duals to uniforms
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Family of uniform n-gonal antiprisms

• v
• t
• e

Antiprism name	Digonal antiprism	(Trigonal) Triangular antiprism	(Tetragonal) Square antiprism	Pentagonal antiprism	Hexagonal antiprism	Heptagonal antiprism	...	Apeirogonal antiprism
Polyhedron image							...
Spherical tiling image							Plane tiling image
Vertex config.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3

Other related polyhedra

Truncation of two opposite vertices results in a square bifrustum.

The octahedron can be generated as the case of a 3D superellipsoid with all exponent values set to 1.

See also

• Octahedral number
• Centered octahedral number
• Spinning octahedron
• Stella octangula
• Triakis octahedron
• Hexakis octahedron
• Truncated octahedron
• Octahedral molecular geometry
• Octahedral symmetry
• Octahedral graph
• Octahedral sphere

Notes

1. (Coxeter 1973) uses the greek letter 𝝓 (phi) to represent one of the three characteristic angles 𝟀, 𝝓, 𝟁 of a regular polytope. Because 𝝓 is commonly used to represent the golden ratio constant ≈ 1.618, for which Coxeter uses 𝝉 (tau), we reverse Coxeter's conventions, and use 𝝉 to represent the characteristic angle.