Top Qs
Timeline
Chat
Perspective
Unit cell
Repeating unit formed by the vectors spanning the points of a lattice From Wikipedia, the free encyclopedia
Remove ads
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice.[1] Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed.
This article needs additional citations for verification. (May 2021) |
The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations.
There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is the smallest possible unit cell.[2] In some cases, the full symmetry of a crystal structure is not obvious from the primitive cell, in which cases a conventional cell may be used. A conventional cell (which may or may not be primitive) is a unit cell with the full symmetry of the lattice and may include more than one lattice point. The conventional unit cells are parallelotopes in n dimensions.
Remove ads
Primitive cell
Summarize
Perspective
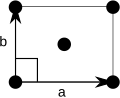
A primitive cell is a unit cell that contains exactly one lattice point. For unit cells generally, lattice points that are shared by n cells are counted as 1/n of the lattice points contained in each of those cells; so for example a primitive unit cell in three dimensions which has lattice points only at its eight vertices is considered to contain 1/8 of each of them.[3] An alternative conceptualization is to consistently pick only one of the n lattice points to belong to the given unit cell (so the other n-1 lattice points belong to adjacent unit cells).
The primitive translation vectors a→1, a→2, a→3 span a lattice cell of smallest volume for a particular three-dimensional lattice, and are used to define a crystal translation vector
where u1, u2, u3 are integers, translation by which leaves the lattice invariant.[note 1] That is, for a point in the lattice r, the arrangement of points appears the same from r′ = r + T→ as from r.[4]
Since the primitive cell is defined by the primitive axes (vectors) a→1, a→2, a→3, the volume Vp of the primitive cell is given by the parallelepiped from the above axes as
Usually, primitive cells in two and three dimensions are chosen to take the shape parallelograms and parallelepipeds, with an atom at each corner of the cell. This choice of primitive cell is not unique, but volume of primitive cells will always be given by the expression above.[5]
Wigner–Seitz cell
In addition to the parallelepiped primitive cells, for every Bravais lattice there is another kind of primitive cell called the Wigner–Seitz cell. In the Wigner–Seitz cell, the lattice point is at the center of the cell, and for most Bravais lattices, the shape is not a parallelogram or parallelepiped. This is a type of Voronoi cell. The Wigner–Seitz cell of the reciprocal lattice in momentum space is called the Brillouin zone.
Remove ads
Conventional cell
For each particular lattice, a conventional cell has been chosen on a case-by-case basis by crystallographers based on convenience of calculation.[6] These conventional cells may have additional lattice points located in the middle of the faces or body of the unit cell. The number of lattice points, as well as the volume of the conventional cell is an integer multiple (1, 2, 3, or 4) of that of the primitive cell.[7]
Remove ads
Two dimensions

For any 2-dimensional lattice, the unit cells are parallelograms, which in special cases may have orthogonal angles, equal lengths, or both. Four of the five two-dimensional Bravais lattices are represented using conventional primitive cells, as shown below.
The centered rectangular lattice also has a primitive cell in the shape of a rhombus, but in order to allow easy discrimination on the basis of symmetry, it is represented by a conventional cell which contains two lattice points.
Three dimensions
Summarize
Perspective

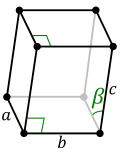
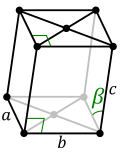
For any 3-dimensional lattice, the conventional unit cells are parallelepipeds, which in special cases may have orthogonal angles, or equal lengths, or both. Seven of the fourteen three-dimensional Bravais lattices are represented using conventional primitive cells, as shown below.
The other seven Bravais lattices (known as the centered lattices) also have primitive cells in the shape of a parallelepiped, but in order to allow easy discrimination on the basis of symmetry, they are represented by conventional cells which contain more than one lattice point.
Remove ads
See also
Notes
- In n dimensions the crystal translation vector would be
Remove ads
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads