Antiprism graph

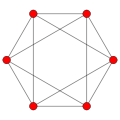
In the mathematical field of graph theory, an antiprism graph is a graph that has one of the antiprisms as its skeleton. An n-sided antiprism has 2n vertices and 4n edges. They are regular, polyhedral (and therefore by necessity also 3-vertex-connected, vertex-transitive, and planar graphs), and also Hamiltonian graphs.^[1]

Examples

The first graph in the sequence, the octahedral graph, has 6 vertices and 12 edges. Later graphs in the sequence may be named after the type of antiprism they correspond to:

• Octahedral graph – 6 vertices, 12 edges
• square antiprismatic graph – 8 vertices, 16 edges
• Pentagonal antiprismatic graph – 10 vertices, 20 edges
• Hexagonal antiprismatic graph – 12 vertices, 24 edges
• Heptagonal antiprismatic graph – 14 vertices, 28 edges
• Octagonal antiprismatic graph – 16 vertices, 32 edges
• ...

3

4

5

6

7

8

Although geometrically the star polygons also form the faces of a different sequence of (self-intersecting) antiprisms, the star antiprisms, they do not form a different sequence of graphs.

Related graphs

An antiprism graph is a special case of a circulant graph, Ci_2n(2,1).

Other infinite sequences of polyhedral graph formed in a similar way from polyhedra with regular-polygon bases include the prism graphs (graphs of prisms) and wheel graphs (graphs of pyramids). Other vertex-transitive polyhedral graphs include the Archimedean graphs.