Brownian excursion

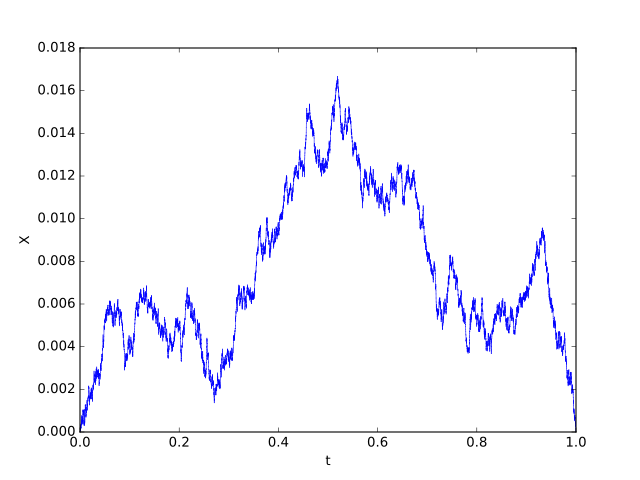
In probability theory a Brownian excursion process (BPE) is a stochastic process that is closely related to a Wiener process (or Brownian motion). Realisations of Brownian excursion processes are essentially just realizations of a Wiener process selected to satisfy certain conditions. In particular, a Brownian excursion process is a Wiener process conditioned to be positive and to take the value 0 at time 1. Alternatively, it is a Brownian bridge process conditioned to be positive. BEPs are important because, among other reasons, they naturally arise as the limit process of a number of conditional functional central limit theorems.^[1]

A realization of Brownian Excursion.

Constructions

Brownian bridge as a union of excursions.

A Brownian excursion process, ${\displaystyle e}$, is a Wiener process (or Brownian motion) conditioned to be positive and to take the value 0 at time 1. Alternatively, it is a Brownian bridge process conditioned to be positive. Although note that, since the probability for an unrestricted Brownian bridge to be positive is zero, the conditioning requires care.

Another representation of a Brownian excursion ${\displaystyle e}$ in terms of a Brownian motion process W (due to Paul Lévy and noted by Kiyosi Itô and Henry P. McKean, Jr.^[2]) is in terms of the last time ${\displaystyle \tau _{-}}$ that W hits zero before time 1 and the first time ${\displaystyle \tau _{+}}$ that Brownian motion ${\displaystyle W}$ hits zero after time 1:^[2]

${\displaystyle \{e(t):\ {0\leq t\leq 1}\}\ {\stackrel {d}{=}}\ \left\{{\frac {|W((1-t)\tau _{-}+t\tau _{+})|}{\sqrt {\tau _{+}-\tau _{-}}}}:\ 0\leq t\leq 1\right\},}$

where the square root is due to the square root self-similarity of Wiener process. That is, ${\displaystyle {\sqrt {a}}W_{t/a}}$ is a Wiener process for any fixed constant ${\displaystyle a>0}$.

Vervaat's transformation.

Let ${\displaystyle \tau _{m}}$ be the time that a Brownian bridge process ${\displaystyle W_{0}}$ achieves its minimum on [0, 1]. Vervaat (1979) shows that

${\displaystyle \{e(t):\ {0\leq t\leq 1}\}\ {\stackrel {d}{=}}\ \left\{W_{0}(\tau _{m}+t{\bmod {1}})-W_{0}(\tau _{m}):\ 0\leq t\leq 1\right\}.}$

This is sometimes called Vervaat's transformation.

Properties

Vervaat's representation of a Brownian excursion has several consequences for various functions of ${\displaystyle e}$. In particular:

${\displaystyle M_{+}\equiv \sup _{0\leq t\leq 1}e(t)\ {\stackrel {d}{=}}\ \sup _{0\leq t\leq 1}W_{0}(t)-\inf _{0\leq t\leq 1}W_{0}(t),}$

(this can also be derived by explicit calculations^[3][4]) and

${\displaystyle \int _{0}^{1}e(t)\,dt\ {\stackrel {d}{=}}\ \int _{0}^{1}W_{0}(t)\,dt-\inf _{0\leq t\leq 1}W_{0}(t).}$

The following result holds:^[5]

${\displaystyle EM_{+}={\sqrt {\pi /2}}\approx 1.25331\ldots ,\,}$

and the following values for the second moment and variance can be calculated by the exact form of the distribution and density:^[5]

${\displaystyle EM_{+}^{2}\approx 1.64493\ldots \ ,\ \ \operatorname {Var} (M_{+})\approx 0.0741337\ldots .}$

Groeneboom (1989), Lemma 4.2 gives an expression for the Laplace transform of (the density) of ${\displaystyle \int _{0}^{1}e(t)\,dt}$. A formula for a certain double transform of the distribution of this area integral is given by Louchard (1984).

Groeneboom (1983) and Pitman (1983) give decompositions of Brownian motion ${\displaystyle W}$ in terms of i.i.d Brownian excursions and the least concave majorant (or greatest convex minorant) of ${\displaystyle W}$.

For an introduction to Itô's general theory of Brownian excursions and the Itô Poisson process of excursions, see Revuz and Yor (1994), chapter XII.

Connections and applications

With probability 1, a Wiener process is continuous, which means the set on which it is non-zero is an open subset of the real line, thus it is the union of countably many Brownian excursions.

The Brownian excursion area

${\displaystyle A_{+}\equiv \int _{0}^{1}e(t)\,dt}$

arises in connection with the enumeration of connected graphs, many other problems in combinatorial theory; see e.g.^{[6][7][8][9][10]} and the limit distribution of the Betti numbers of certain varieties in cohomology theory.^[11] Takacs (1991a) shows that ${\displaystyle A_{+}}$ has density

${\displaystyle f_{A_{+}}(x)={\frac {2{\sqrt {6}}}{x^{2}}}\sum _{j=1}^{\infty }v_{j}^{2/3}e^{-v_{j}}U\left(-{\frac {5}{6}},{\frac {4}{3}};v_{j}\right)\ \ {\text{ with }}\ \ v_{j}={\frac {2|a_{j}|^{3}}{27x^{2}}}}$

where ${\displaystyle a_{j}}$ are the zeros of the Airy function and ${\displaystyle U}$ is the confluent hypergeometric function. Janson and Louchard (2007) show that

${\displaystyle f_{A_{+}}(x)\sim {\frac {72{\sqrt {6}}}{\sqrt {\pi }}}x^{2}e^{-6x^{2}}\ \ {\text{ as }}\ \ x\rightarrow \infty ,}$

and

${\displaystyle P(A_{+}>x)\sim {\frac {6{\sqrt {6}}}{\sqrt {\pi }}}xe^{-6x^{2}}\ \ {\text{ as }}\ \ x\rightarrow \infty .}$

They also give higher-order expansions in both cases.

Janson (2007) gives moments of ${\displaystyle A_{+}}$ and many other area functionals. In particular,

${\displaystyle E(A_{+})={\frac {1}{2}}{\sqrt {\frac {\pi }{2}}},\ \ E(A_{+}^{2})={\frac {5}{12}}\approx 0.416666\ldots ,\ \ \operatorname {Var} (A_{+})={\frac {5}{12}}-{\frac {\pi }{8}}\approx .0239675\ldots \ .}$

Brownian excursions also arise in connection with queuing problems,^[12] railway traffic,^[13][14] and the heights of random rooted binary trees.^[15]

Related processes

• Brownian bridge
• Brownian meander
• reflected Brownian motion
• skew Brownian motion