Budget constraint

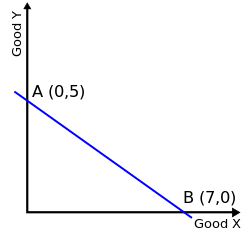
In economics, a budget constraint represents all the combinations of goods and services that a consumer (or other decision-maker) can purchase given current prices and a given level of income or wealth.^[1] In consumer theory, the budget constraint and a preference map (or system of indifference curves) are the basic tools used to analyse consumer choice.^[2] In the standard two-good case, the budget constraint can be represented graphically as a straight line showing the trade-off between the two goods. If ${\displaystyle x}$ and ${\displaystyle y}$ denote the quantities of two goods, with prices ${\displaystyle P_{x}}$ and ${\displaystyle P_{y}}$, and ${\displaystyle m}$ denotes income, the budget line is given by

${\displaystyle P_{x}x+P_{y}y=m.}$

Budget constraint, where ${\displaystyle A={\frac {m}{P_{y}}}}$ and ${\displaystyle B={\frac {m}{P_{x}}}}$

Solving for ${\displaystyle y}$ yields

${\displaystyle y={\frac {m}{P_{y}}}-{\frac {P_{x}}{P_{y}}}\,x,}$

where ${\displaystyle m/P_{y}}$ is the vertical intercept (the maximum amount of ${\displaystyle y}$ the consumer can buy if ${\displaystyle x=0}$) and ${\displaystyle -P_{x}/P_{y}}$ is the slope of the budget line, representing the opportunity cost of one more unit of ${\displaystyle x}$ in terms of ${\displaystyle y}$ forgone.^[1] Similar constraints appear in models of labour–leisure choice, intertemporal consumption, firm behaviour and international trade.^[3][4][5]

Uses in consumer theory

Individual choice

An individual maximises utility at the tangency point (Qx, Qy).

In microeconomic consumer theory, the budget constraint is combined with a description of preferences to study individual utility maximisation. For a given income and price vector, the budget set (all bundles on or below the budget line) represents all the consumption bundles an individual can afford.^[2]

A common assumption is that preferences are well behaved: they are complete, transitive and monotonic, so that "more is better", and that indifference curves are downward-sloping and convex. Under these conditions, the individual's most preferred affordable bundle typically lies at a point where an indifference curve is tangent to the budget line. This tangency point represents the quantities of the two goods that maximise utility subject to the budget constraint.^[1]

However, the optimal bundle need not always be an interior solution. If the tangency point implied by first-order conditions lies outside the feasible set, the optimum will instead be a corner solution at which the consumer consumes only one of the goods, as in the case of perfect substitutes. As income varies, the locus of interior tangency points is called the expansion path.^[6]

Introductory treatments typically assume a linear budget constraint as above. In more realistic settings, budget constraints may be kinked or non-linear because of taxes, subsidies, quantity discounts, rationing, welfare benefits or other institutional features; these cases can also be analysed with the same basic tools, but the geometry and optimality conditions may be more complex.^[7]

In labour economics, the same two-good framework is used to model the trade-off between leisure and consumption. A worker is assumed to have a fixed time endowment that can be allocated between hours of work and hours of leisure; labour income equals the wage rate times hours worked, plus any non-labour income. The wage can then be interpreted as the price of leisure: taking one more hour of leisure reduces labour income, and hence consumption possibilities, by one hour’s wage. The resulting labour–leisure budget line, together with preferences over consumption and leisure, underlies the standard derivation of an individual labour supply curve.^[3][8]

Many goods

While introductory presentations of budget constraints are often limited to two goods because they are easier to illustrate graphically, the idea extends straightforwardly to an arbitrary number of goods. Suppose there are ${\displaystyle n}$ goods, denoted ${\displaystyle x_{i}}$ for ${\displaystyle i=1,\dots ,n}$, with corresponding prices ${\displaystyle p_{i}}$. Let ${\displaystyle W}$ be the total amount that may be spent. The budget constraint is then

${\displaystyle \sum _{i=1}^{n}p_{i}x_{i}\leq W.}$

If the consumer spends the entire amount ${\displaystyle W}$, the budget constraint binds:

${\displaystyle \sum _{i=1}^{n}p_{i}x_{i}=W.}$

In this case, obtaining an additional unit of good ${\displaystyle x_{i}}$ requires reducing consumption of other goods. For example, an additional unit of ${\displaystyle x_{i}}$ can be purchased by giving up ${\displaystyle p_{i}/p_{j}}$ units of good ${\displaystyle x_{j}}$, holding total expenditure fixed. Under standard monotonic preferences, the optimal consumption bundle will lie on the boundary of the budget set (i.e. with the constraint binding), just as in the two-good case.^[1]

Borrowing and lending

Budget constraints can also link consumption across time through borrowing and lending. In a simple two-period setting with interest rate ${\displaystyle r}$, the intertemporal budget constraint can be written as

${\displaystyle c_{1}+{\frac {c_{2}}{1+r}}\leq y_{1}+{\frac {y_{2}}{1+r}},}$

where ${\displaystyle c_{t}}$ and ${\displaystyle y_{t}}$ denote consumption and income in period ${\displaystyle t}$. Borrowing in period 1 allows a consumer to increase current consumption at the cost of reduced consumption in period 2, while saving (lending) has the opposite effect.^[4]

According to behavioural economics, intertemporal choices involving borrowing and lending may also be affected by present bias, in which individuals place disproportionate weight on current consumption relative to future consumption. Models with present-biased preferences often distinguish between sophisticated individuals, who are aware of their present bias, and naïve individuals, who are not.^[9]

Non-linear budget constraints

In many applications, budget constraints are not linear. Progressive income taxes, social insurance contributions, welfare benefits, means-tested benefits, quantity discounts and other institutional features often generate piecewise linear or more complex budget sets, with kinks or notches where effective marginal tax rates change. In labour supply models, for example, the budget line relating hours of work and disposable income typically has different slopes in different ranges of hours because of tax brackets and benefit withdrawal rules. These non-linearities can lead to non-convex budget sets and make optimisation and empirical analysis more complicated, prompting a specialised literature on econometric methods for kinked and non-linear budget constraints.^[7][10]

Other applications

International economics

Point X is unobtainable given the current "budget" constraints on production.

In international economics, an economy's production-possibility frontier (PPF) describes the combinations of two goods that can be produced using available factors of production. Under autarky, the PPF also limits aggregate consumption. With international trade, however, the country can specialise in production and trade at given terms of trade, so that its consumption-possibility frontier (CPF) lies outside the PPF. The CPF in this case plays a role analogous to a budget constraint for the economy as a whole, with a slope determined by the relative price ${\displaystyle P_{x}/P_{y}}$ of exports to imports in standard Heckscher–Ohlin and New Trade Theory models.^[5]

Similar constrained-optimisation problems arise in the theory of the firm. A profit-maximising firm chooses its inputs and outputs subject to a technological production function and cost or budget constraints on the use of inputs. In standard microeconomic models, the firm either maximises profit given input and output prices, or minimises cost for a given level of output, leading to familiar supply and cost curve relationships.^[11][12]

Soft budget constraint

A soft budget constraint describes a situation in which an organisation expects that, if it runs a deficit or faces financial distress, an external actor will cover its shortfall ex post. The external actor is typically a government, higher-level public authority or parent organisation. Because decision-makers do not fully internalise the cost of failure, the budget constraint they face is considered soft compared with a hard budget constraint, under which persistent deficits would lead to bankruptcy, closure or some other credible termination of support.^[13][14]

The term was introduced in the late 1970s by Hungarian economist János Kornai to analyse the behaviour of state-owned enterprises in socialist economies, especially in centrally planned systems. In his account, socialist firms could normally expect to be rescued through subsidies, tax relief, preferential credit, administered prices or the forgiveness of arrears rather than being allowed to fail. This recurring pattern of bailouts created what Kornai called a "soft budget constraint syndrome": firms invested too much, economised too little on costs and lobbied for additional resources instead of adjusting output or employment, contributing to chronic shortages and macroeconomic imbalance.^[13][15]

Subsequent literature has generalised the concept beyond centrally planned economies to transition and market economies. A budget constraint may be soft whenever creditors or sponsors cannot credibly commit to withhold support ex post, for example because the organisation is politically important, systemically significant or provides essential services. The expectation of rescue generates moral hazard: managers may undertake projects that would be rejected under a hard budget constraint and may delay restructuring in the hope of further external assistance. Theoretical work interprets soft budget constraints as a dynamic commitment problem for the sponsor, closely related to other issues of time inconsistency in public finance and industrial policy.^[16][14]

Empirically, soft budget constraints have been studied in a range of settings, including state-owned enterprises, local and regional governments and "too-big-to-fail" financial institutions. In banking, for example, the expectation that authorities will recapitalise distressed institutions or protect their creditors can soften banks' budget constraints and encourage risk-taking, prompting the development of prudential regulation and resolution regimes designed to restore credible limits on public support.^[17][18]

See also

• Choice modelling
• Contingent valuation
• Guns versus butter model
• Heckscher–Ohlin theorem on country-level budget constraints called resource endowments
• Intertemporal budget constraint
• Isoquant
• Opportunity cost
• Scarcity
• Trade-off
• Paternalism