Top Qs
Timeline
Chat
Perspective
Capacitor
Passive two-terminal electronic component that stores electrical energy in an electric field From Wikipedia, the free encyclopedia
Remove ads
A capacitor is a device that stores electrical energy by accumulating electric charges on two closely spaced surfaces that are insulated from each other. It is a passive electronic component with two terminals. A capacitor was originally known as a condenser,[1] a term still encountered in a few compound names, such as the condenser microphone. Colloquially, a capacitor may be called a cap.[2]
The utility of a capacitor depends on its capacitance. While some capacitance exists between any two electrical conductors in proximity in a circuit, a capacitor is a component designed specifically to add capacitance to some part of the circuit.
The physical form and construction of practical capacitors vary widely and many types of capacitor are in common use. Most capacitors contain at least two electrical conductors, often in the form of metallic plates or surfaces separated by a dielectric medium. A conductor may be a foil, thin film, sintered bead of metal, or an electrolyte. The nonconducting dielectric acts to increase the capacitor's charge capacity. Materials commonly used as dielectrics include glass, ceramic, plastic film, paper, mica, air, and oxide layers. When an electric potential difference (a voltage) is applied across the terminals of a capacitor, for example when a capacitor is connected across a battery, an electric field develops across the dielectric, causing a net positive charge to collect on one plate and net negative charge to collect on the other plate. No current actually flows through a perfect dielectric. However, there is a flow of charge through the source circuit. If the condition is maintained sufficiently long, the current through the source circuit ceases. If a time-varying voltage is applied across the leads of the capacitor, the source experiences an ongoing current due to the charging and discharging cycles of the capacitor.
Capacitors are widely used as parts of electrical circuits in many common electrical devices. Unlike a resistor, an ideal capacitor does not dissipate energy, although real-life capacitors do dissipate a small amount .
The earliest forms of capacitors were created in the 1740s, when European experimenters discovered that electric charge could be stored in water-filled glass jars that came to be known as Leyden jars. Today, capacitors are widely used in electronic circuits for blocking direct current while allowing alternating current to pass. In analog filter networks, they smooth the output of power supplies. In resonant circuits they tune radios to particular frequencies. In electric power transmission systems, they stabilize voltage and power flow.[3] The property of energy storage in capacitors was exploited as dynamic memory in early digital computers,[4] and still is in modern DRAM.
The most common example of natural capacitance are the static charges accumulated between clouds in the sky and the surface of the Earth, where the air between them serves as the dielectric. This results in bolts of lightning when the breakdown voltage of the air is exceeded.[5]
Remove ads
History
Summarize
Perspective

In October 1745, Ewald Georg von Kleist of Pomerania, Germany, found that charge could be stored by connecting a high-voltage electrostatic generator by a wire to a volume of water in a hand-held glass jar.[6] Von Kleist's hand and the water acted as conductors and the jar as a dielectric (although details of the mechanism were incorrectly identified at the time). Von Kleist found that touching the wire resulted in a powerful spark, much more painful than that obtained from an electrostatic machine. The following year, the Dutch physicist Pieter van Musschenbroek invented a similar capacitor, which was named the Leyden jar, after the University of Leiden where he worked.[7] He also was impressed by the power of the shock he received, writing, "I would not take a second shock for the kingdom of France."[8]
Daniel Gralath was the first to combine several jars in parallel to increase the charge storage capacity.[9] Benjamin Franklin investigated the Leyden jar and came to the conclusion that the charge was stored on the glass, not in the water as others had assumed. He also adopted the term "battery",[10][11] (denoting the increase of power with a row of similar units as in a battery of cannon), subsequently applied to clusters of electrochemical cells.[12] In 1747, Leyden jars were made by coating the inside and outside of jars with metal foil, leaving a space at the mouth to prevent arcing between the foils.[13] The earliest unit of capacitance was the jar, equivalent to about 1.11 nanofarads.[14]
Leyden jars or more powerful devices employing flat glass plates alternating with foil conductors were used exclusively up until about 1900, when the invention of wireless (radio) created a demand for standard capacitors, and the steady move to higher frequencies required capacitors with lower inductance. More compact construction methods began to be used, such as a flexible dielectric sheet (like oiled paper) sandwiched between sheets of metal foil, rolled or folded into a small package.

Early capacitors were known as condensers, a term that is still occasionally used today, particularly in high power applications, such as automotive systems. The term condensatore was used by Alessandro Volta in 1780 to refer to a device, similar to his electrophorus, he developed to measure electricity, and translated in 1782 as condenser,[15] where the name referred to the device's ability to store a higher density of electric charge than was possible with an isolated conductor.[16][1] The term became deprecated because of the ambiguous meaning of steam condenser, with capacitor being recommended by the British Engineering Standards Association in 1926,[17] although it took several decades for the term to predominate.
Since the beginning of the study of electricity, non-conductive materials like glass, porcelain, paper and mica have been used as insulators. Decades later, these materials were also well-suited for use as the dielectric for the first capacitors. Paper capacitors, made by sandwiching a strip of impregnated paper between strips of metal and rolling the result into a cylinder, were commonly used in the late 19th century; their manufacture started in 1876,[18] and they were used from the early 20th century as decoupling capacitors in telephony.
Porcelain was used in the first ceramic capacitors. In the early years of Marconi's wireless transmitting apparatus, porcelain capacitors were used for high voltage and high frequency application in the transmitters. On the receiver side, smaller mica capacitors were used for resonant circuits. Mica capacitors were invented in 1909 by William Dubilier. Prior to World War II, mica was the most common dielectric for capacitors in the United States.[18]
Charles Pollak (born Karol Pollak), the inventor of the first electrolytic capacitors, found out that the oxide layer on an aluminum anode remained stable in a neutral or alkaline electrolyte, even when the power was switched off. In 1896 he was granted U.S. Patent No. 672,913 for an "Electric liquid capacitor with aluminum electrodes". Solid electrolyte tantalum capacitors were invented by Bell Laboratories in the early 1950s as a miniaturized and more reliable low-voltage support capacitor to complement their newly invented transistor.
With the development of plastic materials by organic chemists during the Second World War, the capacitor industry began to replace paper with thinner polymer films. One very early development in film capacitors was described in British Patent 587,953 in 1944.[18]
Electric double-layer capacitors (now supercapacitors) were invented in 1957 when H. Becker developed a "Low voltage electrolytic capacitor with porous carbon electrodes".[18][19][20] He believed that the energy was stored as a charge in the carbon pores used in his capacitor as in the pores of the etched foils of electrolytic capacitors. Because the double layer mechanism was not known by him at the time, he wrote in the patent: "It is not known exactly what is taking place in the component if it is used for energy storage, but it leads to an extremely high capacity."
The MOS capacitor was later widely adopted as a storage capacitor in memory chips, and as the basic building block of the charge-coupled device (CCD) in image sensor technology.[21] In 1966, Dr. Robert Dennard invented modern DRAM architecture, combining a single MOS transistor per capacitor.[22][23]
Remove ads
Theory of operation
Summarize
Perspective
Overview
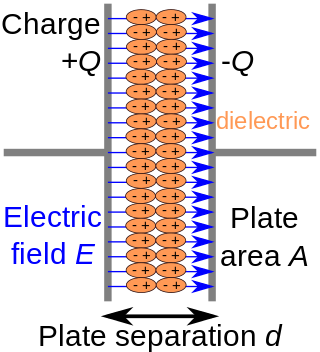

A capacitor consists of two conductors separated by a non-conductive region.[24] The non-conductive region can either be a vacuum or an electrical insulator material known as a dielectric. Examples of dielectric media are glass, air, paper, plastic, ceramic, and even a semiconductor depletion region chemically identical to the conductors. From Coulomb's law, a charge on one conductor will exert a force on the charge carriers within the other conductor, attracting opposite polarity charge and repelling like polarity charges, thus an opposite polarity charge will be induced on the surface of the other conductor. The conductors thus hold equal and opposite charges on their facing surfaces,[25] and the dielectric develops an electric field.
An ideal capacitor is characterized by a constant capacitance C, in farads (F) in the SI system of units, defined as the ratio of the positive or negative charge Q on each conductor to the voltage V between them:[24] A capacitance of one farad (1 F) means that one coulomb of charge on each conductor causes a voltage of one volt across the device.[26] Because the conductors (or plates) are close together, the opposite charges on the conductors attract one another due to their electric fields, allowing the capacitor to store more charge for a given voltage than when the conductors are separated, yielding a larger capacitance.
In practical devices, charge build-up sometimes affects the capacitor mechanically, causing its capacitance to vary. In this case, capacitance is defined in terms of incremental changes:
Hydraulic analogy

In the hydraulic analogy, voltage is analogous to water pressure and electrical current through a wire is analogous to water flow through a pipe. A capacitor is like an elastic diaphragm within the pipe. Although water cannot pass through the diaphragm, it moves as the diaphragm stretches or un-stretches.
- Capacitance is analogous to diaphragm elasticity. In the same way that the ratio of charge differential to voltage would be greater for a larger capacitance value (), the ratio of water displacement to pressure would be greater for a diaphragm that flexes more readily.
- In an AC circuit, a capacitor behaves like a diaphragm in a pipe, allowing the charge to move on both sides of the dielectric while no electrons actually pass through. For DC circuits, a capacitor is analogous to a hydraulic accumulator, storing the energy until pressure is released. Similarly, they can be used to smooth the flow of electricity in rectified DC circuits in the same way an accumulator damps surges from a hydraulic pump.
- Charged capacitors and stretched diaphragms both store potential energy. The more a capacitor is charged, the higher the voltage across the plates (). Likewise, the greater the displaced water volume, the greater the elastic potential energy.
- Electrical current affects the charge differential across a capacitor just as the flow of water affects the volume differential across a diaphragm.
- Just as capacitors experience dielectric breakdown when subjected to high voltages, diaphragms burst under extreme pressures.
- Just as capacitors block DC while passing AC, diaphragms displace no water unless there is a change in pressure.
Circuit equivalence at short-time limit and long-time limit
In a circuit, a capacitor can behave differently at different time instants. However, it is usually easy to think about the short-time limit and long-time limit:
- In the long-time limit, after the charging/discharging current has saturated the capacitor, no current would come into (or get out of) either side of the capacitor; Therefore, the long-time equivalence of capacitor is an open circuit.
- In the short-time limit, if the capacitor starts with a certain voltage V, since the voltage drop on the capacitor is known at this instant, we can replace it with an ideal voltage source of voltage V. Specifically, if V = 0 (capacitor is uncharged), the short-time equivalence of a capacitor is a short circuit.
Parallel-plate capacitor


The simplest model of a capacitor consists of two thin parallel conductive plates each with an area of separated by a uniform gap of thickness filled with a dielectric of permittivity . It is assumed the gap is much smaller than the dimensions of the plates. This model applies well to many practical capacitors which are constructed of metal sheets separated by a thin layer of insulating dielectric, since manufacturers try to keep the dielectric very uniform in thickness to avoid thin spots which can cause failure of the capacitor.
Since the separation between the plates is uniform over the plate area, the electric field between the plates is constant, and directed perpendicularly to the plate surface, except for an area near the edges of the plates where the field decreases because the electric field lines "bulge" out of the sides of the capacitor. This "fringing field" area is approximately the same width as the plate separation, , and assuming is small compared to the plate dimensions, it is small enough to be ignored. Therefore, if a charge of is placed on one plate and on the other plate (the situation for unevenly charged plates is discussed below), the charge on each plate will be spread evenly in a surface charge layer of constant charge density coulombs per square meter, on the inside surface of each plate. From Gauss's law the magnitude of the electric field between the plates is . The voltage (difference) between the plates is defined as the line integral of the electric field over a line (in the z-direction) from one plate to another: The capacitance is defined as . Substituting above into this equation
Therefore, in a capacitor the highest capacitance is achieved with a high permittivity dielectric material, large plate area, and small separation between the plates.
Since the area of the plates increases with the square of the linear dimensions and the separation increases linearly, the capacitance scales with the linear dimension of a capacitor (), or as the cube root of the volume.
A parallel plate capacitor can only store a finite amount of energy before dielectric breakdown occurs. The capacitor's dielectric material has a dielectric strength Ud which sets the capacitor's breakdown voltage at V = Vbd = Udd. The maximum energy that the capacitor can store is therefore
The maximum energy is a function of dielectric volume, permittivity, and dielectric strength. Changing the plate area and the separation between the plates while maintaining the same volume causes no change of the maximum amount of energy that the capacitor can store, so long as the distance between plates remains much smaller than both the length and width of the plates. In addition, these equations assume that the electric field is entirely concentrated in the dielectric between the plates. In reality there are fringing fields outside the dielectric, for example between the sides of the capacitor plates, which increase the effective capacitance of the capacitor. This is sometimes called parasitic capacitance. For some simple capacitor geometries this additional capacitance term can be calculated analytically.[27] It becomes negligibly small when the ratios of plate width to separation and length to separation are large.
For unevenly charged plates:
- If one plate is charged with while the other is charged with , and if both plates are separated from other materials in the environment, then the inner surface of the first plate will have , and the inner surface of the second plated will have charge.[citation needed] Therefore, the voltage between the plates is . Note that the outer surface of both plates will have but those charges do not affect the voltage between the plates.
- If one plate is charged with while the other is charged with , and if the second plate is connected to ground, then the inner surface of the first plate will have , and the inner surface of the second plated will have . Therefore, the voltage between the plates is . Note that the outer surface of both plates will have zero charge.
Interleaved capacitor

For number of plates in a capacitor, the total capacitance would be where is the capacitance for a single plate and is the number of interleaved plates.
As shown to the figure on the right, the interleaved plates can be seen as parallel plates connected to each other. Every pair of adjacent plates acts as a separate capacitor; the number of pairs is always one less than the number of plates, hence the multiplier.
Energy stored in a capacitor
To increase the charge and voltage on a capacitor, work must be done by an external power source to move charge from the negative to the positive plate against the opposing force of the electric field.[28][29] If the voltage on the capacitor is , the work required to move a small increment of charge from the negative to the positive plate is . The energy is stored in the increased electric field between the plates. The total energy stored in a capacitor (expressed in joules) is equal to the total work done in establishing the electric field from an uncharged state.[30][29][28] where is the charge stored in the capacitor, is the voltage across the capacitor, and is the capacitance. This potential energy will remain in the capacitor until the charge is removed. If charge is allowed to move back from the positive to the negative plate, for example by connecting a circuit with resistance between the plates, the charge moving under the influence of the electric field will do work on the external circuit.
If the gap between the capacitor plates is constant, as in the parallel plate model above, the electric field between the plates will be uniform (neglecting fringing fields) and will have a constant value . In this case the stored energy can be calculated from the electric field strength The last formula above is equal to the energy density per unit volume in the electric field multiplied by the volume of field between the plates, confirming that the energy in the capacitor is stored in its electric field.
Current–voltage relation

The current through any component in an electric circuit is defined as the rate of flow of a charge passing through it. Actual charges – electrons – cannot pass through the dielectric of an ideal capacitor.[note 1] Rather, one electron accumulates on the negative plate for each one that leaves the positive plate, resulting in an electron depletion and consequent positive charge on one electrode that is equal and opposite to the accumulated negative charge on the other. Thus the charge on the electrodes is equal to the integral of the current as well as proportional to the voltage, as discussed above. As with any antiderivative, a constant of integration is added to represent the initial voltage ). This is the integral form of the capacitor equation:[31]
Current–voltage relationship (integral form)
Taking the derivative of this and multiplying by yields the derivative form:[32]
Current–voltage relationship (derivative form)
for C independent of time, voltage and electric charge.
The dual of the capacitor is the inductor, which stores energy in a magnetic field rather than an electric field. Its current-voltage relation is obtained by exchanging current and voltage in the capacitor equations and replacing C with the inductance L.
RC circuits

A series circuit containing only a resistor, a capacitor, a switch and a constant DC source of voltage V0 is known as a charging circuit.[33] If the capacitor is initially uncharged while the switch is open, and the switch is closed at t = 0, it follows from Kirchhoff's voltage law that
Taking the derivative and multiplying by C, gives a first-order differential equation:
At t = 0, the voltage across the capacitor is zero and the voltage across the resistor is V0. The initial current is then . With this assumption, solving the differential equation yields where τ0 = RC is the time constant of the system. As the capacitor reaches equilibrium with the source voltage, the voltages across the resistor and the current through the entire circuit decay exponentially. In the case of a discharging capacitor, the capacitor's initial voltage (VCi) replaces V0. The equations become
AC circuits
Impedance, the vector sum of reactance and resistance, describes the phase difference and the ratio of amplitudes between sinusoidally varying voltage and sinusoidally varying current at a given frequency. Fourier analysis allows any signal to be constructed from a spectrum of frequencies, whence the circuit's reaction to the various frequencies may be found. The reactance and impedance of a capacitor are respectively where is the imaginary unit and is the angular frequency of the sinusoidal signal. The phase indicates that the AC voltage lags the AC current by 90°: the positive current phase corresponds to increasing voltage as the capacitor charges; zero current corresponds to instantaneous constant voltage.
Impedance decreases with increasing capacitance and increasing frequency.[34] This implies that a higher-frequency signal or a larger capacitor results in a lower voltage amplitude per current amplitude – an AC "short circuit" or AC coupling. Conversely, for very low frequencies, the reactance is high, so that a capacitor is nearly an open circuit in AC analysis – those frequencies have been "filtered out".
Capacitors are different from resistors and inductors in that the impedance is inversely proportional to the defining characteristic; i.e., capacitance.
A capacitor connected to an alternating voltage source has a displacement current to flowing through it. In the case that the voltage source is , the displacement current can be expressed as:
At , the capacitor has a maximum (or peak) current whereby . The ratio of peak voltage to peak current is due to capacitive reactance (denoted ).
- approaches zero as ω approaches infinity. If approaches 0, the capacitor resembles a short wire that strongly passes current at high frequencies.
- approaches infinity as ω approaches zero. If approaches infinity, the capacitor resembles an open circuit that poorly passes low frequencies.
The current of the capacitor may be expressed in the form of cosines to better compare with the voltage of the source:
In this situation, the current is out of phase with the voltage by radians or +90 degrees, i.e. the current leads the voltage by 90°.
Laplace circuit analysis (s-domain)
When using the Laplace transform in circuit analysis, the impedance of an ideal capacitor with no initial charge is represented in the s domain by: where
- C is the capacitance, and
- s is the complex frequency.
Circuit analysis
Capacitors in parallel
Capacitors in a parallel configuration each have the same applied voltage. Their capacitance values add up. Charge is apportioned among them by capacitance value. Using the schematic diagram to visualize parallel plates, it is apparent that each capacitor contributes to the total surface area.
Capacitors in series
Connected in series, the schematic diagram reveals that the separation distance, not the plate area, adds up. The capacitors each store instantaneous charge build-up equal to that of every other capacitor in the series. The total voltage difference from end to end is apportioned to each capacitor according to the inverse of its capacitance. The entire series acts as a capacitor smaller than any of its components.
Capacitors are combined in series to achieve a higher working voltage, for example for smoothing a high voltage power supply. The voltage ratings, which are based on plate separation, add up, if capacitance and leakage currents for each capacitor are identical. In such an application, on occasion, series strings are connected in parallel, forming a matrix. The goal is to maximize the energy storage of the network without overloading any capacitor. For high-energy storage with capacitors in series, some safety considerations must be applied to ensure one capacitor failing and leaking current does not apply too much voltage to the other series capacitors.
Series connection is also sometimes used to adapt polarized electrolytic capacitors for bipolar AC use.
Voltage distribution in parallel-to-series networks
To model the distribution of voltages from a single charged capacitor (A) connected in parallel to a chain of capacitors in series (Bn):
(Note that this is only correct if all capacitance values are equal).
The power transferred in this arrangement is:
Remove ads
Non-ideal behavior
Summarize
Perspective
In practice, capacitors deviate from the ideal capacitor equation in several aspects. Some of these, such as leakage current and parasitic effects are linear, or can be analyzed as nearly linear, and can be accounted for by adding virtual components to form an equivalent circuit. The usual methods of network analysis can then be applied.[35] In other cases, such as with breakdown voltage, the effect is non-linear and ordinary (normal, e.g., linear) network analysis cannot be used, the effect must be considered separately. Yet another group of artifacts may exist, including temperature dependence, that may be linear but invalidates the assumption in the analysis that capacitance is a constant. Finally, combined parasitic effects such as inherent inductance, resistance, or dielectric losses can exhibit non-uniform behavior at varying frequencies of operation.
Breakdown voltage
Above a particular electric field strength, known as the dielectric strength , the dielectric in a capacitor becomes conductive. The voltage at which this occurs is called the breakdown voltage of the device, and is given by the product of the dielectric strength and the separation between the conductors,[36]
The maximum energy that can be stored safely in a capacitor is limited by the breakdown voltage. Exceeding this voltage can result in a short circuit between the plates, which can often cause permanent damage to the dielectric, plates, or both. Due to the scaling of capacitance and breakdown voltage with dielectric thickness, all capacitors made with a particular dielectric have approximately equal maximum energy density, to the extent that the dielectric dominates their volume.[37]
For air dielectric capacitors the breakdown field strength is of the order 2–5 MV/m (or equivalently in kilovolts per millimeter); for mica the breakdown is 100–300 MV/m; for oil, 15–25 MV/m; it can be much less when other materials are used for the dielectric.[38] The dielectric is used in very thin layers and so absolute breakdown voltage of capacitors is limited. Typical ratings for capacitors used for general electronics applications range from a few volts to 1 kilovolt. As the voltage increases, the dielectric must be thicker, making high-voltage capacitors larger per capacitance than those rated for lower voltages.
The breakdown voltage is critically affected by factors such as the geometry of the capacitor conductive parts; sharp edges or points increase the electric field strength at that point and can lead to a local breakdown. Once this starts to happen, the breakdown quickly tracks through the dielectric until it reaches the opposite plate, leaving carbon behind and causing a short (or relatively low resistance) circuit. The results can be explosive, as the short in the capacitor draws current from the surrounding circuitry and dissipates the energy.[39] However, in capacitors with particular dielectrics[40][41] and thin metal electrodes, shorts are not formed after breakdown. It happens because a metal melts or evaporates in a breakdown vicinity, isolating it from the rest of the capacitor.[42][43]
The usual breakdown route is that the field strength becomes large enough to pull electrons in the dielectric from their atoms thus causing conduction. Other scenarios are possible, such as impurities in the dielectric, and, if the dielectric is of a crystalline nature, imperfections in the crystal structure can result in an avalanche breakdown as seen in semi-conductor devices. Breakdown voltage is also affected by pressure, humidity and temperature.[44]
Equivalent circuit

An ideal capacitor only stores and releases electrical energy, without dissipation. In practice, capacitors have imperfections within the capacitor's materials that result in the following parasitic components:[45]
- , the equivalent series inductance, due to the leads. This is usually significant only at relatively high frequencies.
- Two resistances that add a real-valued component to the total impedance, which wastes power:
- , a small series resistance in the leads. Becomes more relevant as frequency increases.
- , a small conductance (or reciprocally, a large resistance) in parallel with the capacitance, to account for imperfect dielectric material. This causes a small leakage current across the dielectric (see § Leakage)[46] that slowly discharges the capacitor over time. This conductance dominates the total resistance at very low frequencies. Its value varies greatly depending on the capacitor material and quality.[citation needed]
Simplified RLC series model


As frequency increases, the capacitive impedance (a negative reactance) reduces, so the dielectric's conductance becomes less important and the series components become more significant. Thus, a simplified RLC series model valid for a large frequency range simply treats the capacitor as being in series with an equivalent series inductance and a frequency-dependent equivalent series resistance , which varies little with frequency. Unlike the previous model, this model is not valid at DC and very low frequencies where is relevant.
Inductive reactance increases with frequency. Because its sign is positive, it counteracts the capacitance.
At the RLC circuit's natural frequency , the inductance perfectly cancels the capacitance, so total reactance is zero. Since the total impedance at is just the real-value of , average power dissipation reaches its maximum of VRMS2/ESR, where VRMS is the root mean square (RMS) voltage across the capacitor.
At even higher frequencies, the inductive impedance dominates, so the capacitor undesirably behaves instead like an inductor. High-frequency engineering involves accounting for the inductance of all connections and components.
Q factor
For a simplified model of a capacitor as an ideal capacitor in series with an equivalent series resistance , the capacitor's quality factor (or ) is the ratio of the magnitude of its capacitive reactance to its resistance at a given frequency :
The factor is a measure of its efficiency: the higher the factor of the capacitor, the closer it approaches the behavior of an ideal capacitor. Dissipation factor is its reciprocal.
Ripple current
Ripple current is the AC component of an applied source (often a switched-mode power supply) whose frequency may be constant or varying. Ripple current causes heat to be generated within the capacitor due to the dielectric losses caused by the changing field strength together with the current flow across the slightly resistive supply lines or the electrolyte in the capacitor. The equivalent series resistance (ESR) is the amount of internal series resistance one would add to a perfect capacitor to model this.
Some types of capacitors, primarily tantalum and aluminum electrolytic capacitors, as well as some film capacitors have a specified rating value for maximum ripple current.
- Tantalum electrolytic capacitors with solid manganese dioxide electrolyte are limited by ripple current and generally have the highest ESR ratings in the capacitor family. Exceeding their ripple limits can lead to shorts and burning parts.
- Aluminum electrolytic capacitors, the most common type of electrolytic, suffer a shortening of life expectancy at higher ripple currents. If ripple current exceeds the rated value of the capacitor, it tends to result in explosive failure.
- Ceramic capacitors generally have no ripple current limitation[citation needed] and have some of the lowest ESR ratings.
- Film capacitors have very low ESR ratings but exceeding rated ripple current may cause degradation failures.
Capacitance instability
The capacitance of certain capacitors decreases as the component ages. In ceramic capacitors, this is caused by degradation of the dielectric. The type of dielectric, ambient operating and storage temperatures are the most significant aging factors, while the operating voltage usually has a smaller effect, i.e., usual capacitor design is to minimize voltage coefficient. The aging process may be reversed by heating the component above the Curie point. Aging is fastest near the beginning of life of the component, and the device stabilizes over time.[47] Electrolytic capacitors age as the electrolyte evaporates. In contrast with ceramic capacitors, this occurs towards the end of life of the component.
Temperature dependence of capacitance is usually expressed in parts per million (ppm) per °C. It can usually be taken as a broadly linear function but can be noticeably non-linear at the temperature extremes. The temperature coefficient may be positive or negative, depending mostly on the dielectric material. Some, designated C0G/NP0, but called NPO, have a somewhat negative coefficient at one temperature, positive at another, and zero in between. Such components may be specified for temperature-critical circuits.[48]
Capacitors, especially ceramic capacitors, and older designs such as paper capacitors, can absorb sound waves resulting in a microphonic effect. Vibration moves the plates, causing the capacitance to vary, in turn inducing AC current. Some dielectrics also generate piezoelectricity. The resulting interference is especially problematic in audio applications, potentially causing feedback or unintended recording. In the reverse microphonic effect, the varying electric field between the capacitor plates exerts a physical force, moving them as a speaker. This can generate audible sound, but drains energy and stresses the dielectric and the electrolyte, if any.
Current and voltage reversal
Current reversal occurs when the current changes direction. Voltage reversal is the change of polarity in a circuit. Reversal is generally described as the percentage of the maximum rated voltage that reverses polarity. In DC circuits, this is usually less than 100%, often in the range of 0 to 90%, whereas AC circuits experience 100% reversal.
In DC circuits and pulsed circuits, current and voltage reversal are affected by the damping of the system. Voltage reversal is encountered in RLC circuits that are underdamped. The current and voltage reverse direction, forming a harmonic oscillator between the inductance and capacitance. The current and voltage tends to oscillate and may reverse direction several times, with each peak being lower than the previous, until the system reaches an equilibrium. This is often referred to as ringing. In comparison, critically damped or overdamped systems usually do not experience a voltage reversal. Reversal is also encountered in AC circuits, where the peak current is equal in each direction.
For maximum life, capacitors usually need to be able to handle the maximum amount of reversal that a system may experience. An AC circuit experiences 100% voltage reversal, while underdamped DC circuits experience less than 100%. Reversal creates excess electric fields in the dielectric, causes excess heating of both the dielectric and the conductors, and can dramatically shorten the life expectancy of the capacitor. Reversal ratings often affect the design considerations for the capacitor, from the choice of dielectric materials and voltage ratings to the types of internal connections used.[49]
Dielectric absorption
Capacitors made with any type of dielectric material show some level of "dielectric absorption" or "soakage". On discharging a capacitor and disconnecting it, after a short time it may develop a voltage due to hysteresis in the dielectric. This effect is objectionable in applications such as precision sample and hold circuits or timing circuits. The level of absorption depends on many factors, from design considerations to charging time, since the absorption is a time-dependent process. However, the primary factor is the type of dielectric material. Capacitors such as tantalum electrolytic or polysulfone film exhibit relatively high absorption, while polystyrene or Teflon allow very small levels of absorption.[50] In some capacitors where dangerous voltages and energies exist, such as in flashtubes, television sets, microwave ovens and defibrillators, the dielectric absorption can recharge the capacitor to hazardous voltages after it has been shorted or discharged. Any capacitor containing over 10 joules of energy is generally considered hazardous, while 50 joules or higher is potentially lethal. A capacitor may regain anywhere from 0.01 to 20% of its original charge over a period of several minutes, allowing a seemingly safe capacitor to become surprisingly dangerous.[51][52][53][54][55]
Leakage
No material is a perfect insulator, thus all dielectrics allow some small level of current to leak through, which can be measured with a megohmmeter.[56] Leakage is equivalent to a resistor in parallel with the capacitor. Constant exposure to factors such as heat, mechanical stress, or humidity can cause the dielectric to deteriorate resulting in excessive leakage, a problem often seen in older vacuum tube circuits, particularly where oiled paper and foil capacitors were used. In many vacuum tube circuits, interstage coupling capacitors are used to conduct a varying signal from the plate of one tube to the grid circuit of the next stage. A leaky capacitor can cause the grid circuit voltage to be raised from its normal bias setting, causing excessive current or signal distortion in the downstream tube. In power amplifiers this can cause the plates to glow red, or current limiting resistors to overheat, even fail. Similar considerations apply to component fabricated solid-state (transistor) amplifiers, but, owing to lower heat production and the use of modern polyester dielectric-barriers, this once-common problem has become relatively rare.
Electrolytic failure from disuse
Aluminum electrolytic capacitors are conditioned when manufactured by applying a voltage sufficient to initiate the proper internal chemical state. This state is maintained by regular use of the equipment. If a system using electrolytic capacitors is unused for a long period of time it can lose its conditioning. Sometimes they fail with a short circuit when next operated.
Lifespan
All capacitors have varying lifespans, depending upon their construction, operational conditions, and environmental conditions. Solid-state ceramic capacitors generally have very long lives under normal use, which has little dependency on factors such as vibration or ambient temperature, but factors like humidity, mechanical stress, and fatigue play a primary role in their failure. Failure modes may differ. Some capacitors may experience a gradual loss of capacitance, increased leakage or an increase in equivalent series resistance (ESR), while others may fail suddenly or even catastrophically. For example, metal-film capacitors are more prone to damage from stress and humidity, but will self-heal when a breakdown in the dielectric occurs. The formation of a glow discharge at the point of failure prevents arcing by vaporizing the metallic film in that spot, neutralizing any short circuit with minimal loss in capacitance. When enough pinholes accumulate in the film, a total failure occurs in a metal-film capacitor, generally happening suddenly without warning.
Electrolytic capacitors generally have the shortest lifespans. Electrolytic capacitors are affected very little by vibration or humidity, but factors such as ambient and operational temperatures play a large role in their failure, which gradually occur as an increase in ESR (up to 300%) and as much as a 20% decrease in capacitance. The capacitors contain electrolytes which will eventually diffuse through the seals and evaporate. An increase in temperature also increases internal pressure, and increases the reaction rate of the chemicals. Thus, the life of an electrolytic capacitor is generally defined by a modification of the Arrhenius equation, which is used to determine chemical-reaction rates:
Manufacturers often use this equation to supply an expected lifespan, in hours, for electrolytic capacitors when used at their designed operating temperature, which is affected by both ambient temperature, ESR, and ripple current. However, these ideal conditions may not exist in every use. The rule of thumb for predicting lifespan under different conditions of use is determined by:
This says that the capacitor's life decreases by half for every 10 degrees Celsius that the temperature is increased,[57] where:
- is the rated life under rated conditions, e.g. 2000 hours
- is the rated max/min operational temperature
- is the average operational temperature
- is the expected lifespan under given conditions
Remove ads
Capacitor types
Summarize
Perspective
Practical capacitors are available commercially in many different forms. The type of internal dielectric, the structure of the plates and the device packaging all strongly affect the characteristics of the capacitor, and its applications.
Values available range from very low (picofarad range; while arbitrarily low values are in principle possible, stray (parasitic) capacitance in any circuit is the limiting factor) to about 5 kF supercapacitors.
Above approximately 1 microfarad electrolytic capacitors are usually used because of their small size and low cost compared with other types, unless their relatively poor stability, life and polarised nature make them unsuitable. Very high capacity supercapacitors use a porous carbon-based electrode material.
Dielectric materials

Most capacitors have a dielectric spacer, which increases their capacitance compared to air or a vacuum. In order to maximise the charge that a capacitor can hold, the dielectric material needs to have as high a permittivity as possible, while also having as high a breakdown voltage as possible. The dielectric also needs to have as low a loss with frequency as possible.
However, low value capacitors are available with a high vacuum between their plates to allow extremely high voltage operation and low losses. Variable capacitors with their plates open to the atmosphere were commonly used in radio tuning circuits. Later designs use polymer foil dielectric between the moving and stationary plates, with no significant air space between the plates.
Several solid dielectrics are available, including paper, plastic, glass, mica and ceramic.[18]
Paper was used extensively in older capacitors and offers relatively high voltage performance. However, paper absorbs moisture, and has been largely replaced by plastic film capacitors.
Most of the plastic films now used offer better stability and ageing performance than such older dielectrics such as oiled paper, which makes them useful in timer circuits, although they may be limited to relatively low operating temperatures and frequencies, because of the limitations of the plastic film being used. Large plastic film capacitors are used extensively in suppression circuits, motor start circuits, and power-factor correction circuits.
Ceramic capacitors are generally small, cheap and useful for high frequency applications, although their capacitance varies strongly with voltage and temperature and they age poorly. They can also suffer from the piezoelectric effect. Ceramic capacitors are broadly categorized as class 1 dielectrics, which have predictable variation of capacitance with temperature or class 2 dielectrics, which can operate at higher voltage. Modern multilayer ceramics are usually quite small, but some types have inherently wide value tolerances, microphonic issues, and are usually physically brittle.
Glass and mica capacitors are extremely reliable, stable and tolerant to high temperatures and voltages, but are too expensive for most mainstream applications.
Electrolytic capacitors and supercapacitors are used to store small and larger amounts of energy, respectively, ceramic capacitors are often used in resonators, and parasitic capacitance occurs in circuits wherever the simple conductor-insulator-conductor structure is formed unintentionally by the configuration of the circuit layout.


Electrolytic capacitors use an aluminum or tantalum plate with an oxide dielectric layer. The second electrode is a liquid electrolyte, connected to the circuit by another foil plate. Electrolytic capacitors offer very high capacitance but suffer from poor tolerances, high instability, gradual loss of capacitance especially when subjected to heat, and high leakage current. Poor quality capacitors may leak electrolyte, which is harmful to printed circuit boards. The conductivity of the electrolyte drops at low temperatures, which increases equivalent series resistance. While widely used for power-supply conditioning, poor high-frequency characteristics make them unsuitable for many applications. Electrolytic capacitors suffer from self-degradation if unused for a period (around a year), and when full power is applied may short circuit, permanently damaging the capacitor and usually blowing a fuse or causing failure of rectifier diodes. For example, in older equipment, this may cause arcing in rectifier tubes. They can be restored before use by gradually applying the operating voltage, often performed on antique vacuum tube equipment over a period of thirty minutes by using a variable transformer to supply AC power. The use of this technique may be less satisfactory for some solid state equipment, which may be damaged by operation below its normal power range, requiring that the power supply first be isolated from the consuming circuits. Such remedies may not be applicable to modern high-frequency power supplies as these produce full output voltage even with reduced input.[citation needed]
Tantalum capacitors offer better frequency and temperature characteristics than aluminum, but higher dielectric absorption and leakage.[58]
Polymer capacitors (OS-CON, OC-CON, KO, AO) use solid conductive polymer (or polymerized organic semiconductor) as electrolyte and offer longer life and lower ESR at higher cost than standard electrolytic capacitors.
A feedthrough capacitor is a component that, while not serving as its main use, has capacitance and is used to conduct signals through a conductive sheet.
Several other types of capacitor are available for specialist applications. Supercapacitors store large amounts of energy. Supercapacitors made from carbon aerogel, carbon nanotubes, or highly porous electrode materials, offer extremely high capacitance (up to 5 kF as of 2010[update]) and can be used in some applications instead of rechargeable batteries. Alternating current capacitors are specifically designed to work on line (mains) voltage AC power circuits. They are commonly used in electric motor circuits and are often designed to handle large currents, so they tend to be physically large. They are usually ruggedly packaged, often in metal cases that can be easily grounded/earthed. They also are designed with direct current breakdown voltages of at least five times the maximum AC voltage.
Voltage-dependent capacitors
The dielectric constant for a number of very useful dielectrics changes as a function of the applied electrical field, for example ferroelectric materials, so the capacitance for these devices is more complex. For example, in charging such a capacitor the differential increase in voltage with charge is governed by: where the voltage dependence of capacitance, C(V), suggests that the capacitance is a function of the electric field strength, which in a large area parallel plate device is given by ε = V/d. This field polarizes the dielectric, which polarization, in the case of a ferroelectric, is a nonlinear S-shaped function of the electric field, which, in the case of a large area parallel plate device, translates into a capacitance that is a nonlinear function of the voltage.[59][60]
Corresponding to the voltage-dependent capacitance, to charge the capacitor to voltage V an integral relation is found: which agrees with Q = CV only when C does not depend on voltage V.
By the same token, the energy stored in the capacitor now is given by
Integrating: where interchange of the order of integration is used.
The nonlinear capacitance of a microscope probe scanned along a ferroelectric surface is used to study the domain structure of ferroelectric materials.[61]
Another example of voltage dependent capacitance occurs in semiconductor devices such as semiconductor diodes, where the voltage dependence stems not from a change in dielectric constant but in a voltage dependence of the spacing between the charges on the two sides of the capacitor.[62] This effect is intentionally exploited in diode-like devices known as varicaps.
Frequency-dependent capacitors
If a capacitor is driven with a time-varying voltage that changes rapidly enough, at some frequency the polarization of the dielectric cannot follow the voltage. As an example of the origin of this mechanism, the internal microscopic dipoles contributing to the dielectric constant cannot move instantly, and so as frequency of an applied alternating voltage increases, the dipole response is limited and the dielectric constant diminishes. A changing dielectric constant with frequency is referred to as dielectric dispersion, and is governed by dielectric relaxation processes, such as Debye relaxation. Under transient conditions, the displacement field can be expressed as (see electric susceptibility):
indicating the lag in response by the time dependence of εr, calculated in principle from an underlying microscopic analysis, for example, of the dipole behavior in the dielectric. See, for example, linear response function.[63][64] The integral extends over the entire past history up to the present time. A Fourier transform in time then results in:
where εr(ω) is now a complex function, with an imaginary part related to absorption of energy from the field by the medium. See permittivity. The capacitance, being proportional to the dielectric constant, also exhibits this frequency behavior. Fourier transforming Gauss's law with this form for displacement field:
where j is the imaginary unit, V(ω) is the voltage component at angular frequency ω, G(ω) is the real part of the current, called the conductance, and C(ω) determines the imaginary part of the current and is the capacitance. Z(ω) is the complex impedance.
When a parallel-plate capacitor is filled with a dielectric, the measurement of dielectric properties of the medium is based upon the relation: where a single prime denotes the real part and a double prime the imaginary part, Z(ω) is the complex impedance with the dielectric present, Ccmplx(ω) is the so-called complex capacitance with the dielectric present, and C0 is the capacitance without the dielectric.[65][66] (Measurement "without the dielectric" in principle means measurement in free space, an unattainable goal inasmuch as even the quantum vacuum is predicted to exhibit nonideal behavior, such as dichroism. For practical purposes, when measurement errors are taken into account, often a measurement in terrestrial vacuum, or simply a calculation of C0, is sufficiently accurate.[67])
Using this measurement method, the dielectric constant may exhibit a resonance at certain frequencies corresponding to characteristic response frequencies (excitation energies) of contributors to the dielectric constant. These resonances are the basis for a number of experimental techniques for detecting defects. The conductance method measures absorption as a function of frequency.[68] Alternatively, the time response of the capacitance can be used directly, as in deep-level transient spectroscopy.[69]
Another example of frequency dependent capacitance occurs with MOS capacitors, where the slow generation of minority carriers means that at high frequencies the capacitance measures only the majority carrier response, while at low frequencies both types of carrier respond.[62][70]
At optical frequencies, in semiconductors the dielectric constant exhibits structure related to the band structure of the solid. Sophisticated modulation spectroscopy measurement methods based upon modulating the crystal structure by pressure or by other stresses and observing the related changes in absorption or reflection of light have advanced our knowledge of these materials.[71]
Styles

The arrangement of plates and dielectric has many variations in different styles depending on the desired ratings of the capacitor. For small values of capacitance (microfarads and less), ceramic disks use metallic coatings, with wire leads bonded to the coating. Larger values can be made by multiple stacks of plates and disks. Larger value capacitors usually use a metal foil or metal film layer deposited on the surface of a dielectric film to make the plates, and a dielectric film of impregnated paper or plastic – these are rolled up to save space. To reduce the series resistance and inductance for long plates, the plates and dielectric are staggered so that connection is made at the common edge of the rolled-up plates, not at the ends of the foil or metalized film strips that comprise the plates.
The assembly is encased to prevent moisture entering the dielectric – early radio equipment used a cardboard tube sealed with wax. Modern paper or film dielectric capacitors are dipped in a hard thermoplastic. Large capacitors for high-voltage use may have the roll form compressed to fit into a rectangular metal case, with bolted terminals and bushings for connections. The dielectric in larger capacitors is often impregnated with a liquid to improve its properties.

Capacitors may have their connecting leads arranged in many configurations, for example axially or radially. "Axial" means that the leads are on a common axis, typically the axis of the capacitor's cylindrical body – the leads extend from opposite ends. Radial leads are rarely aligned along radii of the body's circle, so the term is conventional. The leads (until bent) are usually in planes parallel to that of the flat body of the capacitor, and extend in the same direction; they are often parallel as manufactured.
Small, cheap discoidal ceramic capacitors have existed from the 1930s onward, and remain in widespread use. After the 1980s, surface mount packages for capacitors have been widely used. These packages are extremely small and lack connecting leads, allowing them to be soldered directly onto the surface of printed circuit boards. Surface mount components avoid undesirable high-frequency effects due to the leads and simplify automated assembly, although manual handling is made difficult due to their small size.
Mechanically controlled variable capacitors allow the plate spacing to be adjusted, for example by rotating or sliding a set of movable plates into alignment with a set of stationary plates. Low cost variable capacitors squeeze together alternating layers of aluminum and plastic with a screw. Electrical control of capacitance is achievable with varactors (or varicaps), which are reverse-biased semiconductor diodes whose depletion region width varies with applied voltage. They are used in phase-locked loops, amongst other applications.
Remove ads
Capacitor markings
Summarize
Perspective
Marking codes for larger parts
Most capacitors have designations printed on their bodies to indicate their electrical characteristics. Larger capacitors, such as electrolytic types usually display the capacitance as value with explicit unit, for example, 220 μF.
For typographical reasons, some manufacturers print MF on capacitors to indicate microfarads (μF).[72]
Three-/four-character marking code for small capacitors
Smaller capacitors, such as ceramic types, often use a shorthand-notation consisting of three digits and an optional letter, where the digits (XYZ) denote the capacitance in picofarad (pF), calculated as XY × 10Z, and the letter indicating the tolerance. Common tolerances are ±5%, ±10%, and ±20%, denotes as J, K, and M, respectively.
A capacitor may also be labeled with its working voltage, temperature, and other relevant characteristics.
Example: A capacitor labeled or designated as 473K 330V has a capacitance of 47×103 pF = 47 nF (±10%) with a maximum working voltage of 330 V. The working voltage of a capacitor is nominally the highest voltage that may be applied across it without undue risk of breaking down the dielectric layer.
Two-character marking code for small capacitors
For capacitances following the E3, E6, E12 or E24 series of preferred values, the former ANSI/EIA-198-D:1991, ANSI/EIA-198-1-E:1998 and ANSI/EIA-198-1-F:2002 as well as the amendment IEC 60062:2016/AMD1:2019 to IEC 60062 define a special two-character marking code for capacitors for very small parts which leave no room to print the above-mentioned three-/four-character code onto them. The code consists of an uppercase letter denoting the two significant digits of the value followed by a digit indicating the multiplier. The EIA standard also defines a number of lowercase letters to specify a number of values not found in E24.[73]
RKM code
The RKM code following IEC 60062 and BS 1852 is a notation to state a capacitor's value in a circuit diagram. It avoids using a decimal separator and replaces the decimal separator with the SI prefix symbol for the particular value (and the letter F for weight 1). The code is also used for part markings. Example: 4n7 for 4.7 nF or 2F2 for 2.2 F.
Historical
In texts prior to the 1960s and on some capacitor packages until more recently,[18] obsolete capacitance units were utilized in electronic books,[75] magazines, and electronics catalogs.[76] The old units "mfd" and "mf" meant microfarad (μF); and the old units "mmfd", "mmf", "uuf", "μμf", "pfd" meant picofarad (pF); but they are rarely used any more.[77] Also, "Micromicrofarad" or "micro-microfarad" are obsolete units that are found in some older texts that is equivalent to picofarad (pF).[75]
Summary of obsolete capacitance units: (upper/lower case variations are not shown)
- μF (microfarad) = mf, mfd
- pF (picofarad) = mmf, mmfd, pfd, μμF
Remove ads
Applications
Summarize
Perspective

Energy storage
A capacitor can store electric energy when disconnected from its charging circuit, so it can be used like a temporary battery, or like other types of rechargeable energy storage system.[78] Capacitors are commonly used in electronic devices to maintain power supply while batteries are being changed. (This prevents loss of information in volatile memory.)
A capacitor can facilitate conversion of kinetic energy of charged particles into electric energy and store it.[79]
There are tradeoffs between capacitors and batteries as storage devices. Without external resistors or inductors, capacitors can generally release their stored energy in a very short time compared to batteries. Conversely, batteries can hold a far greater charge per their size. Conventional capacitors provide less than 360 joules per kilogram of specific energy, whereas a conventional alkaline battery has a density of 590 kJ/kg. There is an intermediate solution: supercapacitors, which can accept and deliver charge much faster than batteries, and tolerate many more charge and discharge cycles than rechargeable batteries. They are, however, 10 times larger than conventional batteries for a given charge. On the other hand, it has been shown that the amount of charge stored in the dielectric layer of the thin film capacitor can be equal to, or can even exceed, the amount of charge stored on its plates.[80]
In car audio systems, large capacitors store energy for the amplifier to use on demand. Also, for a flash tube, a capacitor is used to hold the high voltage.
Digital memory
In the 1930s, John Atanasoff applied the principle of energy storage in capacitors to construct dynamic digital memories for the first binary computers that used electron tubes for logic.[81]
Pulsed power and weapons
Pulsed power is used in many applications to increase the power intensity (watts) of a volume of energy (joules) by releasing that volume within a very short time. Pulses in the nanosecond range and powers in the gigawatts are achievable. Short pulses often require specially constructed, low-inductance, high-voltage capacitors that are often used in large groups (capacitor banks) to supply huge pulses of current for many pulsed power applications. These include electromagnetic forming, Marx generators, pulsed lasers (especially TEA lasers), pulse forming networks, radar, fusion research, and particle accelerators.[82]
Large capacitor banks (reservoir) are used as energy sources for the exploding-bridgewire detonators or slapper detonators in nuclear weapons and other specialty weapons. Experimental work is under way using banks of capacitors as power sources for electromagnetic armour and electromagnetic railguns and coilguns.
Power conditioning

Reservoir capacitors are used in power supplies where they smooth the output of a full or half wave rectifier. They can also be used in charge pump circuits as the energy storage element in the generation of higher voltages than the input voltage.
Capacitors are connected in parallel with the power circuits of most electronic devices and larger systems (such as factories) to shunt away and conceal current fluctuations from the primary power source to provide a "clean" power supply for signal or control circuits. Audio equipment, for example, uses several capacitors in this way, to shunt away power line hum before it gets into the signal circuitry. The capacitors act as a local reserve for the DC power source, and bypass AC currents from the power supply. This is used in car audio applications, when a stiffening capacitor compensates for the inductance and resistance of the leads to the lead–acid car battery.
Power-factor correction

In electric power distribution, capacitors are used for power-factor correction. Such capacitors often come as three capacitors connected as a three phase load. Usually, the values of these capacitors are not given in farads but rather as a reactive power in volt-amperes reactive (var). The purpose is to counteract inductive loading from devices like electric motors and transmission lines to make the load appear to be mostly resistive. Individual motor or lamp loads may have capacitors for power-factor correction, or larger sets of capacitors (usually with automatic switching devices) may be installed at a load center within a building or in a large utility substation.
Suppression and coupling
Signal coupling

Because capacitors pass AC but block DC signals (when charged up to the applied DC voltage), they are often used to separate the AC and DC components of a signal. This method is known as AC coupling or "capacitive coupling". Here, a large value of capacitance, whose value need not be accurately controlled, but whose reactance is small at the signal frequency, is employed.
Decoupling
A decoupling capacitor is a capacitor used to protect one part of a circuit from the effect of another, for instance to suppress noise or transients. Noise caused by other circuit elements is shunted through the capacitor, reducing the effect they have on the rest of the circuit. It is most commonly used between the power supply and ground. An alternative name is bypass capacitor as it is used to bypass the power supply or other high impedance component of a circuit.
Decoupling capacitors need not always be discrete components. Capacitors used in these applications may be built into a printed circuit board, between the various layers. These are often referred to as embedded capacitors.[83] The layers in the board contributing to the capacitive properties also function as power and ground planes, and have a dielectric in between them, enabling them to operate as a parallel plate capacitor.
High-pass and low-pass filters
Noise suppression, spikes, and snubbers
When an inductive circuit is opened, the current through the inductance collapses quickly, creating a large voltage across the open circuit of the switch or relay. If the inductance is large enough, the energy may generate a spark, causing the contact points to oxidize, deteriorate, or sometimes weld together, or destroying a solid-state switch. A snubber capacitor across the newly opened circuit creates a path for this impulse to bypass the contact points, thereby preserving their life; these were commonly found in contact breaker ignition systems, for instance. Similarly, in smaller scale circuits, the spark may not be enough to damage the switch but may still radiate undesirable radio frequency interference (RFI), which a filter capacitor absorbs. Snubber capacitors are usually employed with a low-value resistor in series, to dissipate energy and minimize RFI. Such resistor-capacitor combinations are available in a single package.
Capacitors are also used in parallel with interrupting units of a high-voltage circuit breaker to equally distribute the voltage between these units. These are called "grading capacitors".
In schematic diagrams, a capacitor used primarily for DC charge storage is often drawn vertically in circuit diagrams with the lower, more negative, plate drawn as an arc. The straight plate indicates the positive terminal of the device, if it is polarized (see electrolytic capacitor).
Motor starters
In single phase squirrel cage motors, the primary winding within the motor housing is not capable of starting a rotational motion on the rotor, but is capable of sustaining one. To start the motor, a secondary "start" winding has a series non-polarized starting capacitor to introduce a lead in the sinusoidal current. When the secondary (start) winding is placed at an angle with respect to the primary (run) winding, a rotating electric field is created. The force of the rotational field is not constant, but is sufficient to start the rotor spinning. When the rotor comes close to operating speed, a centrifugal switch (or current-sensitive relay in series with the main winding) disconnects the capacitor. The start capacitor is typically mounted to the side of the motor housing. These are called capacitor-start motors, that have relatively high starting torque. Typically they can have up-to four times as much starting torque as a split-phase motor and are used on applications such as compressors, pressure washers and any small device requiring high starting torques.
Capacitor-run induction motors have a permanently connected phase-shifting capacitor in series with a second winding. The motor is much like a two-phase induction motor.
Motor-starting capacitors are typically non-polarized electrolytic types, while running capacitors are conventional paper or plastic film dielectric types.
Signal processing
The energy stored in a capacitor can be used to represent information, either in binary form, as in DRAMs, or in analogue form, as in analog sampled filters and CCDs. Capacitors can be used in analog circuits as components of integrators or more complex filters and in negative feedback loop stabilization. Signal processing circuits also use capacitors to integrate a current signal.
Tuned circuits
Capacitors and inductors are applied together in tuned circuits to select information in particular frequency bands. For example, radio receivers rely on variable capacitors to tune the station frequency. Speakers use passive analog crossovers, and analog equalizers use capacitors to select different audio bands.
The resonant frequency f of a tuned circuit is a function of the inductance (L) and capacitance (C) in series, and is given by: where L is in henries and C is in farads.
Sensing
Most capacitors are designed to maintain a fixed physical structure. However, various factors can change the structure of the capacitor, and the resulting change in capacitance can be used to sense those factors.
- Changing the dielectric
- The effects of varying the characteristics of the dielectric can be used for sensing purposes. Capacitors with an exposed and porous dielectric can be used to measure humidity in air. Capacitors are used to accurately measure the fuel level in airplanes; as the fuel covers more of a pair of plates, the circuit capacitance increases. Squeezing the dielectric can change a capacitor at a few tens of bar pressure sufficiently that it can be used as a pressure sensor.[84] A selected, but otherwise standard, polymer dielectric capacitor, when immersed in a compatible gas or liquid, can work usefully as a very low cost pressure sensor up to many hundreds of bar.
- Changing the distance between the plates
- Capacitors with a flexible plate can be used to measure strain or pressure. Industrial pressure transmitters used for process control use pressure-sensing diaphragms, which form a capacitor plate of an oscillator circuit. Capacitors are used as the sensor in condenser microphones, where one plate is moved by air pressure, relative to the fixed position of the other plate. Some accelerometers use MEMS capacitors etched on a chip to measure the magnitude and direction of the acceleration vector. They are used to detect changes in acceleration, in tilt sensors, or to detect free fall, as sensors triggering airbag deployment, and in many other applications. Some fingerprint sensors use capacitors. Additionally, a user can adjust the pitch of a theremin musical instrument by moving their hand since this changes the effective capacitance between the user's hand and the antenna.
- Changing the effective area of the plates
- Capacitive touch switches are used on many consumer electronic products.
Oscillators

A capacitor can possess spring-like qualities in an oscillator circuit. In the image example, a capacitor acts to influence the biasing voltage at the npn transistor's base. The resistance values of the voltage-divider resistors and the capacitance value of the capacitor together control the oscillatory frequency.
Producing light
A light-emitting capacitor is made from a dielectric that uses phosphorescence to produce light. If one of the conductive plates is made with a transparent material, the light is visible. Light-emitting capacitors are used in the construction of electroluminescent panels, for applications such as backlighting for laptop computers. In this case, the entire panel is a capacitor used for the purpose of generating light.
Remove ads
Hazards and safety
Summarize
Perspective
The hazards posed by a capacitor are usually determined by the amount of energy stored, which can cause electrical burns or heart fibrillation. Factors such as voltage and chassis material are of secondary consideration, which are more related to how easily a shock can be initiated rather than how much damage can occur.[55] Although they usually do not leave a burn, shocks as low as one joule have been reported to cause death under certain conditions, including conductivity of the surfaces, preexisting medical conditions, the humidity of the air, or the pathways it takes through the body (i.e. shocks that travel across the core of the body and, especially, through the heart are more dangerous than those limited to the extremities). Shocks over ten joules generally damage skin, and are considered hazardous. Any capacitor that can store 50 joules or more is considered potentially lethal.[85][55]
Capacitors may retain a charge long after power is removed from a circuit; this charge can cause dangerous or fatal shocks or damage connected equipment. For example, the flash of a disposable camera has a photoflash capacitor that may contain over 15 joules of energy and be charged to over 300 volts. Service procedures for electronic devices usually include instructions to discharge large or high-voltage capacitors. Larger capacitors may have built-in discharge resistors to dissipate stored energy to a safe level within a few seconds after power is removed. High-voltage capacitors are stored with the terminals shorted, as protection from potentially dangerous voltages due to dielectric absorption or from transient voltages the capacitor may pick up from static charges or passing weather events.[55]

Some old, large oil-filled paper or plastic film capacitors contain polychlorinated biphenyls (PCBs) which can leak into groundwater from landfills. Capacitors containing PCBs were labelled as containing "Askarel" and several other trade names. PCB-filled paper capacitors are found in pre-1975 fluorescent lamp ballasts, and other applications. Such capacitors may be sealed in a metal can with ceramic feed-through connectors.
Capacitors may catastrophically fail when subjected to voltages or currents beyond their rating, or in case of polarized capacitors, applied in a reverse polarity. Failures may create arcing that heats and vaporizes the dielectric fluid, causing a build up of pressurized gas that may result in swelling, rupture, or an explosion. Larger capacitors may have vents or similar mechanism to release of pressure in the event of failure. Capacitors used in RF or sustained high-current applications can overheat, especially in the center of the capacitor rolls. Capacitors used within high-energy capacitor banks can violently explode when a short in one capacitor causes sudden dumping of energy stored in the rest of the bank into the failing unit. High voltage vacuum capacitors can generate soft X-rays even during normal operation. Proper containment, fusing, and preventive maintenance can help to minimize these hazards.
High-voltage capacitors may benefit from a pre-charge to limit in-rush currents at power-up of high voltage direct current (HVDC) circuits. This extends the life of the component and may mitigate high-voltage hazards.
- Swollen electrolytic capacitors. The vent on the tops allows the release of pressurized gas build-up in the event of failure, preventing it from exploding.
- This high-energy capacitor from a defibrillator has a resistor connected between the terminals for safety, to dissipate stored energy.
- An exploded electrolytic capacitor, showing fragments of paper and metallic foil
Remove ads
See also
Notes
- Most real capacitors may have a small dielectric leakage current that passes through the resistive dielectric layer in between the plates.
- In order to reduce the risk for read errors, the letters
IandOare not used as their glyphs look similar to other letters and digits.
References
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

























































































![{\displaystyle \mathop {} \!\mathrm {d} W=Q\mathop {} \!\mathrm {d} V=\left[\int _{0}^{V}\mathop {} \!\mathrm {d} V'\,C(V')\right]\mathop {} \!\mathrm {d} V.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b83994840f075db5c87dba510df4e9a0721ee93c)



![{\displaystyle {\begin{aligned}I(\omega )&=j\omega Q(\omega )=j\omega \oint _{\Sigma }{\boldsymbol {D}}({\boldsymbol {r}},\omega )\cdot \mathop {} \!\mathrm {d} {\boldsymbol {\Sigma }}\\&=\left[G(\omega )+j\omega C(\omega )\right]V(\omega )={\frac {V(\omega )}{Z(\omega )}}\,,\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e02e712969ddff783c02db53271a903cc730109b)




