Capsule (geometry)

A capsule (from Latin capsula, "small box or chest"), or stadium of revolution, is a basic three-dimensional geometric shape consisting of a cylinder with hemispherical ends.^[1] Another name for this shape is spherocylinder.^[2][3][4][5]

A two-dimensional orthographic projection at the left with a three-dimensional one at the right depicting a capsule

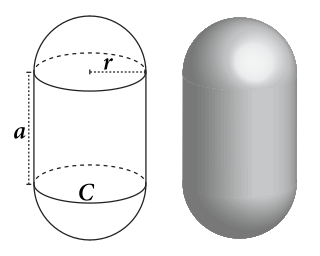
It can also be referred to as an oval although the sides (either vertical or horizontal) are straight parallel.

Usages

The shape is used for some objects like containers for pressurised gases, building domes, and pharmaceutical capsules.

In chemistry and physics, this shape is used as a basic model for non-spherical particles. It appears, in particular as a model for the molecules in liquid crystals^[6][3][4] or for the particles in granular matter.^[5][7][8]

Formulas

The volume ${\displaystyle V}$ of a capsule is calculated by adding the volume of a ball of radius ${\displaystyle r}$ (that accounts for the two hemispheres) to the volume of the cylindrical part. Hence, if the cylinder has height ${\displaystyle h}$,

${\displaystyle V={\frac {4}{3}}\pi r^{3}+(\pi r^{2}h)=\pi r^{2}\left({\frac {4}{3}}r+h\right)}$.

The surface area of a capsule of radius ${\displaystyle r}$ whose cylinder part has height ${\displaystyle h}$ is ${\displaystyle 2\pi r(2r+h)}$.

Generalization

A capsule can be equivalently described as the Minkowski sum of a ball of radius ${\displaystyle r}$ with a line segment of length ${\displaystyle a}$.^[5] By this description, capsules can be straightforwardly generalized as Minkowski sums of a ball with a polyhedron. The resulting shape is called a spheropolyhedron.^[7][8]

Related shapes

A capsule is the three-dimensional shape obtained by revolving the two-dimensional stadium around the line of symmetry that bisects the semicircles.