Chamfered dodecahedron

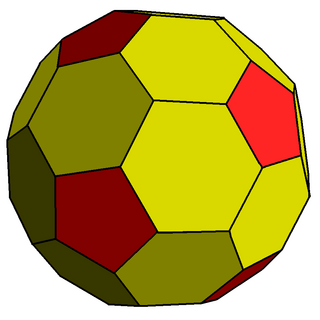
In geometry, the chamfered dodecahedron is a convex polyhedron with 80 vertices, 120 edges, and 42 faces: 30 hexagons and 12 pentagons. It is constructed as a chamfer (edge-truncation) of a regular dodecahedron. The pentagons are reduced in size and new hexagonal faces are added in place of all the original edges. Its dual is the pentakis icosidodecahedron.

Chamfered dodecahedron
Type	Goldberg polyhedron (GV(2,0) = {5+,3}2,0) Fullerene (C80)[1] Near-miss Johnson solid
Faces	12 pentagons 30 irregular hexagons
Edges	120 (2 types)
Vertices	80 (2 types)
Vertex configuration	60 (5.6.6) 20 (6.6.6)
Conway notation	cD = t5daD = dk5aD
Symmetry group	Icosahedral (Ih)
Dual polyhedron	Pentakis icosidodecahedron
Properties	convex, equilateral-faced
Net

It is also called a truncated rhombic triacontahedron, constructed as a truncation of the rhombic triacontahedron. It can more accurately be called an order-5 truncated rhombic triacontahedron because only the order-5 vertices are truncated.

Structure

These 12 order-5 vertices can be truncated such that all edges are equal length. The original 30 rhombic faces become non-regular hexagons, and the truncated vertices become regular pentagons.

The hexagon faces can be equilateral but not regular with D₂ symmetry. The angles at the two vertices with vertex configuration 6.6.6 are ${\displaystyle \arccos \left({\frac {-1}{\sqrt {5}}}\right)\approx 116.565^{\circ }}$ and at the remaining four vertices with 5.6.6, they are ≈121.717° each.

It is the Goldberg polyhedron G_V(2,0), containing pentagonal and hexagonal faces.

It also represents the exterior envelope of a cell-centered orthogonal projection of the 120-cell, one of six convex regular 4-polytopes.

Chemistry

The chamfered dodecahedron is the shape of the fullerene C₈₀. Ocassionally, this shape is denoted C₈₀(I_h), describing its icosahedral symmetry and distinguishing it from other less-symmetric 80-vertex fullerenes.^[2] It is one of only four fullerenes found by Deza, Deza & Grishukhin (1998) to have a skeleton that can be isometrically embeddable into an L₁ space.^[3]

chamfered dodecahedron

Related polyhedra

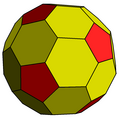
This polyhedron looks very similar to the uniform truncated icosahedron, which has 12 pentagons, but only 20 hexagons.

• 
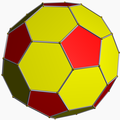
  Truncated rhombic triacontahedron
  G(2,0)
• 
  Truncated icosahedron
  G(1,1)
• 
  cell-centered orthogonal projection of the 120-cell

Related polytopes

It represents the exterior envelope of a cell-centered orthogonal projection of the 120-cell, one of six convex regular 4-polytopes, into 3 dimensions.