Top Qs
Timeline
Chat
Perspective
Complex network
Network with non-trivial topological features From Wikipedia, the free encyclopedia
Remove ads
In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in networks representing real systems. The study of complex networks is a young and active area of scientific research[1][2] (since 2000) inspired largely by empirical findings of real-world networks such as computer networks, biological networks, technological networks, brain networks,[3][4] climate networks[5] and social networks.[6]
Remove ads
Definition
Summarize
Perspective
Most social, biological, and technological networks display substantial non-trivial topological features, with patterns of connection between their elements that are neither purely regular nor purely random. Such features include a heavy tail in the degree distribution, a high clustering coefficient, assortativity or disassortativity among vertices, community structure, and hierarchical structure. In the case of directed networks these features also include reciprocity, triad significance profile and other features. In contrast, many of the mathematical models of networks that have been studied in the past, such as lattices and random graphs, do not show these features. The most complex structures can be realized by networks with a medium number of interactions.[7] This corresponds to the fact that the maximum information content (entropy) is obtained for medium probabilities.
Two well-known and much studied classes of complex networks are scale-free networks[8] and small-world networks,[9][10] whose discovery and definition are canonical case-studies in the field. Both are characterized by specific structural features—power-law degree distributions for the former and short path lengths and high clustering for the latter. However, as the study of complex networks has continued to grow in importance and popularity, many other aspects of network structures have attracted attention as well.
The field continues to develop at a brisk pace, and has brought together researchers from many areas including mathematics, physics, electric power systems,[11] biology, climate, computer science, sociology, epidemiology, and others.[12] Ideas and tools from network science and engineering have been applied to the analysis of metabolic and genetic regulatory networks; the study of ecosystem stability and robustness;[13] clinical science;[14] the modeling and design of scalable communication networks such as the generation and visualization of complex wireless networks;[15] and a broad range of other practical issues. Network science is the topic of many conferences in a variety of different fields, and has been the subject of numerous books both for the lay person and for the expert.
Remove ads
Scale-free networks
Summarize
Perspective
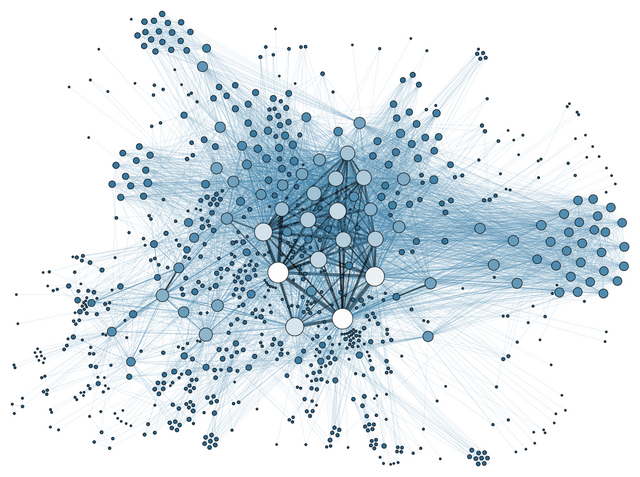
A network is called scale-free[8][16] if its degree distribution, i.e., the probability that a node selected uniformly at random has a certain number of links (degree), follows a mathematical function called a power law. The power law implies that the degree distribution of these networks has no characteristic scale. In contrast, networks with a single well-defined scale are somewhat similar to a lattice in that every node has (roughly) the same degree. Examples of networks with a single scale include the Erdős–Rényi (ER) random graph, random regular graphs, regular lattices, and hypercubes. Some models of growing networks that produce scale-invariant degree distributions are the Barabási–Albert model and the fitness model. In a network with a scale-free degree distribution, some vertices have a degree that is orders of magnitude larger than the average - these vertices are often called "hubs", although this language is misleading as, by definition, there is no inherent threshold above which a node can be viewed as a hub. If there were such a threshold, the network would not be scale-free.
Interest in scale-free networks began in the late 1990s with the reporting of discoveries of power-law degree distributions in real world networks such as the World Wide Web, the network of Autonomous systems (ASs), some networks of Internet routers, protein interaction networks, email networks, etc. Most of these reported "power laws" fail when challenged with rigorous statistical testing, but the more general idea of heavy-tailed degree distributions—which many of these networks do genuinely exhibit (before finite-size effects occur) -- are very different from what one would expect if edges existed independently and at random (i.e., if they followed a Poisson distribution). There are many different ways to build a network with a power-law degree distribution. The Yule process is a canonical generative process for power laws, and has been known since 1925. However, it is known by many other names due to its frequent reinvention, e.g., The Gibrat principle by Herbert A. Simon, the Matthew effect, cumulative advantage and, preferential attachment by Barabási and Albert for power-law degree distributions. Recently, Hyperbolic Geometric Graphs have been suggested as yet another way of constructing scale-free networks.
Some networks with a power-law degree distribution (and specific other types of structure) can be highly resistant to the random deletion of vertices—i.e., the vast majority of vertices remain connected together in a giant component. Such networks can also be quite sensitive to targeted attacks aimed at fracturing the network quickly. When the graph is uniformly random except for the degree distribution, these critical vertices are the ones with the highest degree, and have thus been implicated in the spread of disease (natural and artificial) in social and communication networks, and in the spread of fads (both of which are modeled by a percolation or branching process). While random graphs (ER) have an average distance of order log N[9] between nodes, where N is the number of nodes, scale free graph can have a distance of log log N.
Remove ads
Small-world networks
Summarize
Perspective
A network is called a small-world network[9] by analogy with the small-world phenomenon (popularly known as six degrees of separation). The small world hypothesis, which was first described by the Hungarian writer Frigyes Karinthy in 1929, and tested experimentally by Stanley Milgram (1967), is the idea that two arbitrary people are connected by only six degrees of separation, i.e. the diameter of the corresponding graph of social connections is not much larger than six. In 1998, Duncan J. Watts and Steven Strogatz published the first small-world network model, which through a single parameter smoothly interpolates between a random graph and a lattice.[9] Their model demonstrated that with the addition of only a small number of long-range links, a regular graph, in which the diameter is proportional to the size of the network, can be transformed into a "small world" in which the average number of edges between any two vertices is very small (mathematically, it should grow as the logarithm of the size of the network), while the clustering coefficient stays large. It is known that a wide variety of abstract graphs exhibit the small-world property, e.g., random graphs and scale-free networks. Further, real world networks such as the World Wide Web and the metabolic network also exhibit this property.
In the scientific literature on networks, there is some ambiguity associated with the term "small world". In addition to referring to the size of the diameter of the network, it can also refer to the co-occurrence of a small diameter and a high clustering coefficient. The clustering coefficient is a metric that represents the density of triangles in the network. For instance, sparse random graphs have a vanishingly small clustering coefficient while real world networks often have a coefficient significantly larger. Scientists point to this difference as suggesting that edges are correlated in real world networks. Approaches have been developed to generate network models that exhibit high correlations, while preserving the desired degree distribution and small-world properties. These approaches can be used to generate analytically solvable toy models for research into these systems.[17]
Remove ads
Spatial networks
Many real networks are embedded in space. Examples include, transportation and other infrastructure networks, brain networks.[3][4] Several models for spatial networks have been developed.[18]
See also
- Community structure
- Complex adaptive system
- Complex systems
- Dual-phase evolution
- Dynamic network analysis
- Interdependent networks
- Multidimensional network
- Network theory
- Network science
- Percolation theory
- Random graph
- Random graph theory of gelation
- Scale-free networks
- Small world networks
- Spatial network
- Trophic coherence
Books
- Zinilli, A. (2025). Elements of Network Science: Theory, Methods and Applications in Stata, R and Python. Cham: Springer. https://doi.org/10.1007/978-3-031-84712-7
- B. S. Manoj, Abhishek Chakraborty, and Rahul Singh, Complex Networks: A Networking and Signal Processing Perspective, Pearson, New York, USA, February 2018. ISBN 978-0-13-478699-5
- S.N. Dorogovtsev and J.F.F. Mendes, Evolution of Networks: From biological networks to the Internet and WWW, Oxford University Press, 2003, ISBN 0-19-851590-1
- Duncan J. Watts, Six Degrees: The Science of a Connected Age, W. W. Norton & Company, 2003, ISBN 0-393-04142-5
- Duncan J. Watts, Small Worlds: The Dynamics of Networks between Order and Randomness, Princeton University Press, 2003, ISBN 0-691-11704-7
- Albert-László Barabási, Linked: How Everything is Connected to Everything Else, 2004, ISBN 0-452-28439-2
- Alain Barrat, Marc Barthelemy, Alessandro Vespignani, Dynamical processes on complex networks, Cambridge University Press, 2008, ISBN 978-0-521-87950-7
- Stefan Bornholdt (editor) and Heinz Georg Schuster (editor), Handbook of Graphs and Networks: From the Genome to the Internet, 2003, ISBN 3-527-40336-1
- Guido Caldarelli, Scale-Free Networks, Oxford University Press, 2007, ISBN 978-0-19-921151-7
- Guido Caldarelli, Michele Catanzaro, Networks: A Very Short Introduction Oxford University Press, 2012, ISBN 978-0-19-958807-7
- E. Estrada, "The Structure of Complex Networks: Theory and Applications", Oxford University Press, 2011, ISBN 978-0-199-59175-6
- Mark Newman, Networks: An Introduction, Oxford University Press, 2010, ISBN 978-0-19-920665-0
- Mark Newman, Albert-László Barabási, and Duncan J. Watts, The Structure and Dynamics of Networks, Princeton University Press, Princeton, 2006, ISBN 978-0-691-11357-9
- R. Pastor-Satorras and A. Vespignani, Evolution and Structure of the Internet: A statistical physics approach, Cambridge University Press, 2004, ISBN 0-521-82698-5
- T. Lewis, Network Science, Wiley 2009,
- Niloy Ganguly (editor), Andreas Deutsch (editor) and Animesh Mukherjee (editor), Dynamics On and Of Complex Networks Applications to Biology, Computer Science, and the Social Sciences, 2009, ISBN 978-0-8176-4750-6
- Vito Latora, Vincenzo Nicosia, Giovanni Russo, Complex Networks: Principles, Methods and Applications, Cambridge University Press, 2017, ISBN 978-1-107-10318-4
Remove ads
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
