Top Qs
Timeline
Chat
Perspective
Continuous function
Mathematical function with no sudden changes From Wikipedia, the free encyclopedia
Remove ads
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as discontinuities. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is not continuous. Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity.
Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their definition is the basis of topology.
A stronger form of continuity is uniform continuity. In order theory, especially in domain theory, a related concept of continuity is Scott continuity.
As an example, the function H(t) denoting the height of a growing flower at time t would be considered continuous. In contrast, the function M(t) denoting the amount of money in a bank account at time t would be considered discontinuous since it "jumps" at each point in time when money is deposited or withdrawn.
Remove ads
History
A form of the epsilon–delta definition of continuity was first given by Bernard Bolzano in 1817. Augustin-Louis Cauchy defined continuity of as follows: an infinitely small increment of the independent variable x always produces an infinitely small change of the dependent variable y (see e.g. Cours d'Analyse, p. 34). Cauchy defined infinitely small quantities in terms of variable quantities, and his definition of continuity closely parallels the infinitesimal definition used today (see microcontinuity). The formal definition and the distinction between pointwise continuity and uniform continuity were first given by Bolzano in the 1830s, but the work wasn't published until the 1930s. Like Bolzano,[1] Karl Weierstrass[2] denied continuity of a function at a point c unless it was defined at and on both sides of c, but Édouard Goursat[3] allowed the function to be defined only at and on one side of c, and Camille Jordan[4] allowed it even if the function was defined only at c. All three of those nonequivalent definitions of pointwise continuity are still in use.[5] Eduard Heine provided the first published definition of uniform continuity in 1872, but based these ideas on lectures given by Peter Gustav Lejeune Dirichlet in 1854.[6]
Remove ads
Real functions
Summarize
Perspective
Definition

A real function that is a function from real numbers to real numbers can be represented by a graph in the Cartesian plane; such a function is continuous if, roughly speaking, the graph is a single unbroken curve whose domain is the entire real line. A more mathematically rigorous definition is given below.[8]
Continuity of real functions is usually defined in terms of limits. A function f with variable x is continuous at the real number c, if the limit of as x tends to c, is equal to
There are several different definitions of the (global) continuity of a function, which depend on the nature of its domain.
A function is continuous on an open interval if the interval is contained in the function's domain and the function is continuous at every interval point. A function that is continuous on the interval (the whole real line) is often called simply a continuous function; one also says that such a function is continuous everywhere. For example, all polynomial functions are continuous everywhere.
A function is continuous on a semi-open or a closed interval; if the interval is contained in the domain of the function, the function is continuous at every interior point of the interval, and the value of the function at each endpoint that belongs to the interval is the limit of the values of the function when the variable tends to the endpoint from the interior of the interval. For example, the function is continuous on its whole domain, which is the semi-open interval
Many commonly encountered functions are partial functions that have a domain formed by all real numbers, except some isolated points. Examples include the reciprocal function and the tangent function When they are continuous on their domain, one says, in some contexts, that they are continuous, although they are not continuous everywhere. In other contexts, mainly when one is interested in their behavior near the exceptional points, one says they are discontinuous.
A partial function is discontinuous at a point if the point belongs to the topological closure of its domain, and either the point does not belong to the domain of the function or the function is not continuous at the point. For example, the functions and are discontinuous at 0, and remain discontinuous whichever value is chosen for defining them at 0. A point where a function is discontinuous is called a discontinuity.
Using mathematical notation, several ways exist to define continuous functions in the three senses mentioned above.
Let be a function whose domain is contained in of real numbers.
Some (but not all) possibilities for are:
- is the whole real line; that is,
- is a closed interval of the form where a and b are real numbers
- is an open interval of the form where a and b are real numbers
In the case of an open interval, and do not belong to , and the values and are not defined, and if they are, they do not matter for continuity on .
Definition in terms of limits of functions
The function f is continuous at some point c of its domain if the limit of as x approaches c through the domain of f, exists and is equal to [9] In mathematical notation, this is written as In detail this means three conditions: first, f has to be defined at c (guaranteed by the requirement that c is in the domain of f). Second, the limit of that equation has to exist. Third, the value of this limit must equal
(Here, we have assumed that the domain of f does not have any isolated points.)
Definition in terms of neighborhoods
A neighborhood of a point c is a set that contains, at least, all points within some fixed distance of c. Intuitively, a function is continuous at a point c if the range of f over the neighborhood of c shrinks to a single point as the width of the neighborhood around c shrinks to zero. More precisely, a function f is continuous at a point c of its domain if, for any neighborhood there is a neighborhood in its domain such that whenever
As neighborhoods are defined in any topological space, this definition of a continuous function applies not only for real functions but also when the domain and the codomain are topological spaces and is thus the most general definition. It follows that a function is automatically continuous at every isolated point of its domain. For example, every real-valued function on the integers is continuous.
Definition in terms of limits of sequences

One can instead require that for any sequence of points in the domain which converges to c, the corresponding sequence converges to In mathematical notation,
Weierstrass and Jordan definitions (epsilon–delta) of continuous functions

Explicitly including the definition of the limit of a function, we obtain a self-contained definition: Given a function as above and an element of the domain , is said to be continuous at the point when the following holds: For any positive real number however small, there exists some positive real number such that for all in the domain of with the value of satisfies
Alternatively written, continuity of at means that for every there exists a such that for all :
More intuitively, we can say that if we want to get all the values to stay in some small neighborhood around we need to choose a small enough neighborhood for the values around If we can do that no matter how small the neighborhood is, then is continuous at
In modern terms, this is generalized by the definition of continuity of a function with respect to a basis for the topology, here the metric topology.
Weierstrass had required that the interval be entirely within the domain , but Jordan removed that restriction.
Definition in terms of control of the remainder
In proofs and numerical analysis, we often need to know how fast limits are converging, or in other words, control of the remainder. We can formalize this to a definition of continuity. A function is called a control function if
- C is non-decreasing
A function is C-continuous at if there exists such a neighbourhood that
A function is continuous in if it is C-continuous for some control function C.
This approach leads naturally to refining the notion of continuity by restricting the set of admissible control functions. For a given set of control functions a function is -continuous if it is -continuous for some For example, the Lipschitz, the Hölder continuous functions of exponent α and the uniformly continuous functions below are defined by the set of control functions respectively.
Definition using oscillation

Continuity can also be defined in terms of oscillation: a function f is continuous at a point if and only if its oscillation at that point is zero;[10] in symbols, A benefit of this definition is that it quantifies discontinuity: the oscillation gives how much the function is discontinuous at a point.
This definition is helpful in descriptive set theory to study the set of discontinuities and continuous points – the continuous points are the intersection of the sets where the oscillation is less than (hence a set) – and gives a rapid proof of one direction of the Lebesgue integrability condition.[11]
The oscillation is equivalent to the definition by a simple re-arrangement and by using a limit (lim sup, lim inf) to define oscillation: if (at a given point) for a given there is no that satisfies the definition, then the oscillation is at least and conversely if for every there is a desired the oscillation is 0. The oscillation definition can be naturally generalized to maps from a topological space to a metric space.
Definition using the hyperreals
Cauchy defined the continuity of a function in the following intuitive terms: an infinitesimal change in the independent variable corresponds to an infinitesimal change of the dependent variable (see Cours d'analyse, page 34). Non-standard analysis is a way of making this mathematically rigorous. The real line is augmented by adding infinite and infinitesimal numbers to form the hyperreal numbers. In nonstandard analysis, continuity can be defined as follows.
A real-valued function f is continuous at x if its natural extension to the hyperreals has the property that for all infinitesimal dx, is infinitesimal[12]
(see microcontinuity). In other words, an infinitesimal increment of the independent variable always produces an infinitesimal change of the dependent variable, giving a modern expression to Augustin-Louis Cauchy's definition of continuity.
Rules for continuity

Proving the continuity of a function by a direct application of the definition is generally a noneasy task. Fortunately, in practice, most functions are built from simpler functions, and their continuity can be deduced immediately from the way they are defined, by applying the following rules:
- Every constant function is continuous
- The identity function is continuous
- Addition and multiplication: If the functions and are continuous on their respective domains and , then their sum and their product are continuous on the intersection , where and are defined by and .
- Reciprocal: If the function is continuous on the domain , then its reciprocal , defined by is continuous on the domain , that is, the domain from which the points such that are removed.
- Function composition: If the functions and are continuous on their respective domains and , then the composition defined by is continuous on , that the part of that is mapped by inside .
- The sine and cosine functions ( and ) are continuous everywhere.
- The exponential function is continuous everywhere.
- The natural logarithm is continuous on the domain formed by all positive real numbers .

These rules imply that every polynomial function is continuous everywhere and that a rational function is continuous everywhere where it is defined, if the numerator and the denominator have no common zeros. More generally, the quotient of two continuous functions is continuous outside the zeros of the denominator.

An example of a function for which the above rules are not sufficient is the sinc function, which is defined by and for . The above rules show immediately that the function is continuous for , but, for proving the continuity at , one has to prove As this is true, one gets that the sinc function is continuous function on all real numbers.
Examples of discontinuous functions

An example of a discontinuous function is the Heaviside step function , defined by
Pick for instance . Then there is no -neighborhood around , i.e. no open interval with that will force all the values to be within the -neighborhood of , i.e. within . Intuitively, we can think of this type of discontinuity as a sudden jump in function values.
Similarly, the signum or sign function is discontinuous at but continuous everywhere else. Yet another example: the function is continuous everywhere apart from .

Besides plausible continuities and discontinuities like above, there are also functions with a behavior, often coined pathological, for example, Thomae's function, is continuous at all irrational numbers and discontinuous at all rational numbers. In a similar vein, Dirichlet's function, the indicator function for the set of rational numbers, is nowhere continuous.
Properties
A useful lemma
Let be a function that is continuous at a point and be a value such Then throughout some neighbourhood of [13]
Proof: By the definition of continuity, take , then there exists such that Suppose there is a point in the neighbourhood for which then we have the contradiction
Intermediate value theorem
The intermediate value theorem is an existence theorem, based on the real number property of completeness, and states:
- If the real-valued function f is continuous on the closed interval and k is some number between and then there is some number such that
For example, if a child grows from 1 m to 1.5 m between the ages of two and six years, then, at some time between two and six years of age, the child's height must have been 1.25 m.
As a consequence, if f is continuous on and and differ in sign, then, at some point must equal zero.
Extreme value theorem
The extreme value theorem states that if a function f is defined on a closed interval (or any closed and bounded set) and is continuous there, then the function attains its maximum, i.e. there exists with for all The same is true of the minimum of f. These statements are not, in general, true if the function is defined on an open interval (or any set that is not both closed and bounded), as, for example, the continuous function defined on the open interval (0,1), does not attain a maximum, being unbounded above.
Relation to differentiability and integrability
Every differentiable function is continuous, as can be shown. The converse does not hold: for example, the absolute value function
is everywhere continuous. However, it is not differentiable at (but is so everywhere else). Weierstrass's function is also everywhere continuous but nowhere differentiable.
The derivative f′(x) of a differentiable function f(x) need not be continuous. If f′(x) is continuous, f(x) is said to be continuously differentiable. The set of such functions is denoted More generally, the set of functions (from an open interval (or open subset of ) to the reals) such that f is times differentiable and such that the -th derivative of f is continuous is denoted See differentiability class. In the field of computer graphics, properties related (but not identical) to are sometimes called (continuity of position), (continuity of tangency), and (continuity of curvature); see Smoothness of curves and surfaces.
Every continuous function is integrable (for example in the sense of the Riemann integral). The converse does not hold, as the (integrable but discontinuous) sign function shows.
Pointwise and uniform limits

Given a sequence of functions such that the limit exists for all , the resulting function is referred to as the pointwise limit of the sequence of functions The pointwise limit function need not be continuous, even if all functions are continuous, as the animation at the right shows. However, f is continuous if all functions are continuous and the sequence converges uniformly, by the uniform convergence theorem. This theorem can be used to show that the exponential functions, logarithms, square root function, and trigonometric functions are continuous.
Directional Continuity
Discontinuous functions may be discontinuous in a restricted way, giving rise to the concept of directional continuity (or right and left continuous functions) and semi-continuity. Roughly speaking, a function is right-continuous if no jump occurs when the limit point is approached from the right. Formally, f is said to be right-continuous at the point c if the following holds: For any number however small, there exists some number such that for all x in the domain with the value of satisfies
This is the same condition as continuous functions, except it is required to hold only for x strictly larger than c. Requiring to hold instead for all x with yields the notion of left-continuous functions. A function is continuous if and only if it is both right-continuous and left-continuous.
Semicontinuity
A function f is lower semi-continuous at the point c if, roughly, any jumps that might occur only go down, but not up. That is, for any there exists some number such that for all x in the domain with the value of satisfies The reverse condition is upper semi-continuity.
Remove ads
Continuous functions between metric spaces
Summarize
Perspective
The concept of continuous real-valued functions can be generalized to functions between metric spaces. A metric space is a set equipped with a function (called metric) that can be thought of as a measurement of the distance of any two elements in X. Formally, the metric is a function that satisfies a number of requirements, notably the triangle inequality. Given two metric spaces and and a function then is continuous at the point (with respect to the given metrics) if for any positive real number there exists a positive real number such that all satisfying will also satisfy As in the case of real functions above, this is equivalent to the condition that for every sequence in with limit we have The latter condition can be weakened as follows: is continuous at the point if and only if for every convergent sequence in with limit , the sequence is a Cauchy sequence, and is in the domain of .
The set of points at which a function between metric spaces is continuous is a set – this follows from the definition of continuity.
This notion of continuity is applied, for example, in functional analysis. A key statement in this area says that a linear operator between normed vector spaces and (which are vector spaces equipped with a compatible norm, denoted ) is continuous if and only if it is bounded, that is, there is a constant such that for all
Uniform, Hölder and Lipschitz continuity

The concept of continuity for functions between metric spaces can be strengthened in various ways by limiting the way depends on and c in the definition above. Intuitively, a function f as above is uniformly continuous if the does not depend on the point c. More precisely, it is required that for every real number there exists such that for every with we have that Thus, any uniformly continuous function is continuous. The converse does not generally hold but holds when the domain space X is compact. Uniformly continuous maps can be defined in the more general situation of uniform spaces.[14]
A function is Hölder continuous with exponent α (a real number) if there is a constant K such that for all the inequality holds. Any Hölder continuous function is uniformly continuous. The particular case is referred to as Lipschitz continuity. That is, a function is Lipschitz continuous if there is a constant K such that the inequality holds for any [15] The Lipschitz condition occurs, for example, in the Picard–Lindelöf theorem concerning the solutions of ordinary differential equations.
Remove ads
Continuous functions between topological spaces
Summarize
Perspective
Another, more abstract, notion of continuity is the continuity of functions between topological spaces in which there generally is no formal notion of distance, as there is in the case of metric spaces. A topological space is a set X together with a topology on X, which is a set of subsets of X satisfying a few requirements with respect to their unions and intersections that generalize the properties of the open balls in metric spaces while still allowing one to talk about the neighborhoods of a given point. The elements of a topology are called open subsets of X (with respect to the topology).
A function between two topological spaces X and Y is continuous if for every open set the inverse image is an open subset of X. That is, f is a function between the sets X and Y (not on the elements of the topology ), but the continuity of f depends on the topologies used on X and Y.
This is equivalent to the condition that the preimages of the closed sets (which are the complements of the open subsets) in Y are closed in X.
An extreme example: if a set X is given the discrete topology (in which every subset is open), all functions to any topological space T are continuous. On the other hand, if X is equipped with the indiscrete topology (in which the only open subsets are the empty set and X) and the space T set is at least T0, then the only continuous functions are the constant functions. Conversely, any function whose codomain is indiscrete is continuous.
Continuity at a point
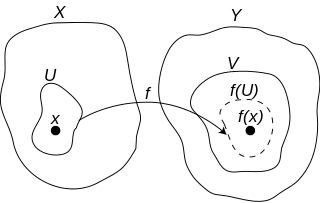
The translation in the language of neighborhoods of the -definition of continuity leads to the following definition of the continuity at a point:
A function is continuous at a point if and only if for any neighborhood V of in Y, there is a neighborhood U of such that
This definition is equivalent to the same statement with neighborhoods restricted to open neighborhoods and can be restated in several ways by using preimages rather than images. One of those ways is the following. As every set that contains a neighborhood is also a neighborhood, and is the largest subset such that the above definition may be simplified into:
A function is continuous at a point if and only if is a neighborhood of for every neighborhood V of in Y.
As an open set is a set that is a neighborhood of all its points, a function is continuous at every point of X if and only if it is a continuous function.
If X and Y are metric spaces, it is equivalent to consider the neighborhood system of open balls centered at x and f(x) instead of all neighborhoods. This gives back the above definition of continuity in the context of metric spaces. In general topological spaces, there is no notion of nearness or distance. If, however, the target space is a Hausdorff space, it is still true that f is continuous at a if and only if the limit of f as x approaches a is f(a). At an isolated point, every function is continuous.
Given a map is continuous at if and only if whenever is a filter on that converges to in which is expressed by writing then necessarily in If denotes the neighborhood filter at then is continuous at if and only if in [16] Moreover, this happens if and only if the prefilter is a filter base for the neighborhood filter of in [16]
Alternative definitions
Several equivalent definitions for a topological structure exist; thus, several equivalent ways exist to define a continuous function.
Sequences and nets
In several contexts, the topology of a space is conveniently specified in terms of limit points. This is often accomplished by specifying when a point is the limit of a sequence. Still, for some spaces that are too large in some sense, one specifies also when a point is the limit of more general sets of points indexed by a directed set, known as nets. A function is (Heine-)continuous only if it takes limits of sequences to limits of sequences. In the former case, preservation of limits is also sufficient; in the latter, a function may preserve all limits of sequences yet still fail to be continuous, and preservation of nets is a necessary and sufficient condition.
In detail, a function is sequentially continuous if whenever a sequence in converges to a limit the sequence converges to Thus, sequentially continuous functions "preserve sequential limits." Every continuous function is sequentially continuous. If is a first-countable space and countable choice holds, then the converse also holds: any function preserving sequential limits is continuous. In particular, if is a metric space, sequential continuity and continuity are equivalent. For non-first-countable spaces, sequential continuity might be strictly weaker than continuity. (The spaces for which the two properties are equivalent are called sequential spaces.) This motivates the consideration of nets instead of sequences in general topological spaces. Continuous functions preserve the limits of nets, and this property characterizes continuous functions.
For instance, consider the case of real-valued functions of one real variable:[17]
Theorem—A function is continuous at if and only if it is sequentially continuous at that point.
Closure operator and interior operator definitions
In terms of the interior and closure operators, we have the following equivalences,
Theorem—Let be a mapping between topological spaces. Then the following are equivalent.
- is continuous;
- for every subset
- for every subset
If we declare that a point is close to a subset if then this terminology allows for a plain English description of continuity: is continuous if and only if for every subset maps points that are close to to points that are close to Similarly, is continuous at a fixed given point if and only if whenever is close to a subset then is close to
Instead of specifying topological spaces by their open subsets, any topology on can alternatively be determined by a closure operator or by an interior operator. Specifically, the map that sends a subset of a topological space to its topological closure satisfies the Kuratowski closure axioms. Conversely, for any closure operator there exists a unique topology on (specifically, ) such that for every subset is equal to the topological closure of in If the sets and are each associated with closure operators (both denoted by ) then a map is continuous if and only if for every subset
Similarly, the map that sends a subset of to its topological interior defines an interior operator. Conversely, any interior operator induces a unique topology on (specifically, ) such that for every is equal to the topological interior of in If the sets and are each associated with interior operators (both denoted by ) then a map is continuous if and only if for every subset [18]
Filters and prefilters
Continuity can also be characterized in terms of filters. A function is continuous if and only if whenever a filter on converges in to a point then the prefilter converges in to This characterization remains true if the word "filter" is replaced by "prefilter."[16]
Properties
If and are continuous, then so is the composition If is continuous and
- X is compact, then f(X) is compact.
- X is connected, then f(X) is connected.
- X is path-connected, then f(X) is path-connected.
- X is Lindelöf, then f(X) is Lindelöf.
- X is separable, then f(X) is separable.
The possible topologies on a fixed set X are partially ordered: a topology is said to be coarser than another topology (notation: ) if every open subset with respect to is also open with respect to Then, the identity map is continuous if and only if (see also comparison of topologies). More generally, a continuous function stays continuous if the topology is replaced by a coarser topology and/or is replaced by a finer topology.
Homeomorphisms
Symmetric to the concept of a continuous map is an open map, for which images of open sets are open. If an open map f has an inverse function, that inverse is continuous, and if a continuous map g has an inverse, that inverse is open. Given a bijective function f between two topological spaces, the inverse function need not be continuous. A bijective continuous function with a continuous inverse function is called a homeomorphism.
If a continuous bijection has as its domain a compact space and its codomain is Hausdorff, then it is a homeomorphism.
Defining topologies via continuous functions
Given a function where X is a topological space and S is a set (without a specified topology), the final topology on S is defined by letting the open sets of S be those subsets A of S for which is open in X. If S has an existing topology, f is continuous with respect to this topology if and only if the existing topology is coarser than the final topology on S. Thus, the final topology is the finest topology on S that makes f continuous. If f is surjective, this topology is canonically identified with the quotient topology under the equivalence relation defined by f.
Dually, for a function f from a set S to a topological space X, the initial topology on S is defined by designating as an open set every subset A of S such that for some open subset U of X. If S has an existing topology, f is continuous with respect to this topology if and only if the existing topology is finer than the initial topology on S. Thus, the initial topology is the coarsest topology on S that makes f continuous. If f is injective, this topology is canonically identified with the subspace topology of S, viewed as a subset of X.
A topology on a set S is uniquely determined by the class of all continuous functions into all topological spaces X. Dually, a similar idea can be applied to maps
Remove ads
Related notions
Summarize
Perspective
If is a continuous function from some subset of a topological space then a continuous extension of to is any continuous function such that for every , which is a condition that is often written as . In words, it is any continuous function that restricts to on . This notion is used, for example, in the Tietze extension theorem and the Hahn–Banach theorem. If is not continuous, then it could not possibly have a continuous extension. If is a Hausdorff space and is a dense subset of then a continuous extension of to , if one exists, will be unique. The Blumberg theorem states that if is an arbitrary function then there exists a dense subset of such that the restriction is continuous; in other words, every function can be restricted to some dense subset on which it is continuous.
Various other mathematical domains use the concept of continuity in different but related meanings. For example, in order theory, an order-preserving function between particular types of partially ordered sets and is continuous if for each directed subset of we have Here is the supremum with respect to the orderings in and respectively. This notion of continuity is the same as topological continuity when the partially ordered sets are given the Scott topology.[19][20]
In category theory, a functor between two categories is called continuous if it commutes with small limits. That is to say, for any small (that is, indexed by a set as opposed to a class) diagram of objects in .
A continuity space is a generalization of metric spaces and posets,[21][22] which uses the concept of quantales, and that can be used to unify the notions of metric spaces and domains.[23]
In measure theory, a function defined on a Lebesgue measurable set is called approximately continuous at a point if the approximate limit of at exists and equals . This generalizes the notion of continuity by replacing the ordinary limit with the approximate limit. A fundamental result known as the Stepanov-Denjoy theorem states that a function is measurable if and only if it is approximately continuous almost everywhere.[24]
Remove ads
See also
- Continuity (mathematics)
- Absolute continuity
- Approximate continuity
- Dini continuity
- Equicontinuity
- Geometric continuity
- Parametric continuity
- Classification of discontinuities
- Coarse function
- Continuous function (set theory)
- Continuous stochastic process
- Normal function
- Open and closed maps
- Piecewise
- Squeeze mapping
- Symmetrically continuous function
- Direction-preserving function - an analog of a continuous function in discrete spaces.
Remove ads
References
Bibliography
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads


















![{\displaystyle D=[a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\},}](http://wikimedia.org/api/rest_v1/media/math/render/svg/dc3f2152a27a96fd31caeae439cba949a53a0b67)






























![{\displaystyle C:[0,\infty )\to [0,\infty ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/96dbec0587155c14584a3c95ebf835b19a3fa57b)






































































![{\displaystyle [a,b],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2d493b840f8326ba81ff9d95b4edf1effd5f2842)

![{\displaystyle c\in [a,b],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/657c696455d34f8f86aad0515088771fe0d1f229)

![{\displaystyle [a,b]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle c\in [a,b]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/997256364b06acf0710e5d24da39e8c42991a249)

![{\displaystyle x\in [a,b].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/584ca2ac74e6072c1f7e88ab8f79d523ff8e22a2)













![{\displaystyle f:[a,b]\to \mathbb {R} }](http://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)
























































































 ...
...












































































