Transimpedance amplifier

In electronics, a transimpedance amplifier (TIA) is a current to voltage converter, almost exclusively implemented with one or more operational amplifiers (opamps). The TIA can be used to amplify^[1] the current output of Geiger–Müller tubes, photo multiplier tubes, accelerometers, photodetectors and other sensors (that are modeled well as a current source) into a usable voltage.

Fig. 1. Simple transimpedance amplifier which converts an input current source I_in into a voltage output V_out.

Current to voltage converters are used with sensors that have a current response to their measured physical quantity that is more linear than their voltage response. This is the case with photodiodes where it is not uncommon for the current response to have better than 1% nonlinearity over a wide range of light input.

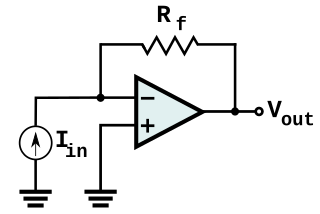
The transimpedance amplifier presents a low impedance to the sensor and isolates it from the output voltage of the operational amplifier. In its simplest form (Fig. 1), a transimpedance amplifier is just an opamp with a large-valued feedback resistor, R_f. This resistor sets the amplifier's transimpedance (i.e. its change in output voltage divided by its change in input current, sometimes simply referred to as "gain") to -R_f. This is negative since the amplifier is in an inverting configuration.

There are several different configurations of transimpedance amplifiers, each suited to a particular application. The one factor they all have in common is the requirement to convert the low-level current of a sensor to a voltage. The gain, bandwidth, as well as current and voltage offsets change with different types of sensors, requiring different configurations of transimpedance amplifiers.^[2]

DC operation

In the circuit shown in Figure 1, a sensor (represented as a current source) such as a photodiode is connected between ground and the inverting input of the opamp. The other input of the opamp is also connected to ground, so the non-inverting input becomes a virtual ground. This provides a low-impedance load for the photodiode, which keeps the photodiode voltage low. The photodiode operates in photovoltaic mode with no external bias. The high gain of the opamp keeps the photodiode current equal to the feedback current through R_f. The input offset voltage due to the photodiode is very low in this self-biased photovoltaic mode. This permits a large gain without any large output offset voltage. This configuration is used with photodiodes that are illuminated with low light levels and require a lot of gain.

The DC and low-frequency gain of a transimpedance amplifier is determined by the equation

${\displaystyle -I_{\text{in}}={\frac {V_{\text{out}}}{R_{\text{f}}}},}$

so

${\displaystyle {\frac {V_{\text{out}}}{I_{\text{in}}}}=-R_{\text{f}}.}$

This ratio is in units of resistance, which in SI units are ohms (Ω), and is more technically called transimpedance instead of gain (which is a dimensionless quantity). If the gain is large, any input offset voltage at the non-inverting input of the opamp will result in an output DC offset. An input bias current on the inverting terminal of the opamp will similarly result in an output offset. To minimize these effects, transimpedance amplifiers are usually designed with field-effect transistor (FET) input opamps that have very low input offset voltages.^[3]

Fig. 2. Transimpedance amplifier with a reverse-biased photodiode

An inverting TIA can also be used with the photodiode operating in the photoconductive mode, as shown in Figure 2. A positive voltage at the cathode of the photodiode applies a reverse bias. This reverse bias increases the width of the depletion region and lowers the junction capacitance, improving the high-frequency performance. The photoconductive configuration of a transimpedance photodiode amplifier is used where higher bandwidth is required. The feedback capacitor C_f is usually necessary to improve stability.

Bandwidth and stability

Fig. 3. Incremental model showing sensor capacitance ${\displaystyle C_{\text{i}}}$ and a feedback capacitor ${\displaystyle C_{\text{f}}}$.

The frequency response of a transimpedance amplifier is inversely proportional to the gain set by the feedback resistor. The sensors which transimpedance amplifiers are used with usually have more capacitance than an opamp can handle. The sensor can be modeled as a current source in parallel with a capacitance ${\displaystyle C_{\text{i}}}$, as shown in Figure 3.^[4] This capacitance across the input terminals of the opamp, which includes the internal capacitance of the opamp, introduces a low-pass filter in the feedback path. The low-pass frequency response of this filter can be characterized as the feedback factor:

${\displaystyle \beta ={\frac {1}{1+R_{\text{f}}C_{\text{i}}s}},}$

When the effect of this low-pass filter response is considered, the circuit's response equation becomes:

${\displaystyle V_{\text{out}}=I_{\text{p}}{\frac {-R_{\text{f}}}{1+{\frac {1}{A_{\text{OL}}\beta }}}},}$

where ${\displaystyle A_{\text{OL}}}$ is the open-loop gain of the opamp.

At low frequencies the feedback factor β has little effect on the amplifier response. The amplifier response will be close to the ideal:

${\displaystyle V_{\text{out}}=-I_{\text{p}}R_{\text{f}}}$

as long as the loop gain ${\displaystyle (A_{\text{OL}}\beta )}$ is much greater than unity.

Without compensation

Fig. 4. Bode plot of uncompensated transimpedance amplifier^[5]

In the Bode plot (Fig. 4) of a transimpedance amplifier with no compensation, the flat curve with the peak, labeled I-to-V gain, is the frequency response of the transimpedance amplifier. The peaking of the gain curve is typical of uncompensated or poorly compensated transimpedance amplifiers. The curve labeled A_OL is the open-loop response of the amplifier. The feedback factor, plotted as a reciprocal, is labeled 1/β.

The 1/β and A_OL curves intersect to form an isosceles triangle with the frequency axis. The two sides have equal but opposite slopes, since one is the result of a first-order pole, and the other of a first-order zero. Each slope has a magnitude of 20 dB/decade, corresponding to a phase shift of 90°. When the amplifier's 180° of phase inversion is added to this, the result is a full 360° at the f_i intercept, indicated by the dashed vertical line. At that intercept, 1/β = A_OL for a loop gain of A_OLβ = 1. Oscillation will occur at the frequency f_i because of the 360° phase shift, or positive feedback, and the unity gain.^[6]

With compensation

To mitigate these effects, designers of transimpedance amplifiers add a small-value compensating capacitor (${\displaystyle C_{\text{f}}}$ in Fig. 3) in parallel with the feedback resistor. When this feedback capacitor is considered, the compensated feedback factor becomes

${\displaystyle \beta ={\frac {1+R_{\text{f}}C_{\text{f}}s}{1+R_{\text{f}}(C_{\text{i}}+C_{\text{f}})s}}.}$

Fig. 5. Bode plot of compensated transimpedance amplifier^[7]

The feedback capacitor produces a zero, or deflection in the response curve, at the frequency

${\displaystyle f_{C_{\text{f}}}={\frac {1}{2\pi R_{\text{f}}C_{\text{f}}}}.}$

This counteracts the pole produced by C_i at the frequency

${\displaystyle f_{\text{zf}}={\frac {1}{2\pi R_{\text{f}}(C_{\text{i}}+C_{\text{f}})}}.}$

The Bode plot of a transimpedance amplifier with a compensation capacitor in the feedback path is shown in Fig. 5. The compensated feedback factor is plotted as a reciprocal, 1/β, and starts to roll off before f_i, reducing the slope at the intercept. The loop gain is still unity, but the total phase shift is not a full 360°. One of the requirements for oscillation is eliminated with the addition of the compensation capacitor, and so the circuit has stability. This also reduces the gain peaking, producing a flatter overall response.

There are several methods used to calculate the compensation capacitor's value. Excessive capacitance will reduce the amplifier's bandwidth, while too little capacitance may produce oscillation.^[8] One difficulty with this method of phase compensation is the resulting small value of the capacitor, and the iterative method often required to optimize the value. There is no explicit formula for calculating the capacitor value that works for all cases. A compensation method that uses a larger-value capacitor that is not as susceptible to parasitic capacitance effects can also be used.^[9]

Noise considerations

A TIA's input-referred voltage noise consists of flicker noise (a.k.a. 1/f noise), which dominates at lower frequencies, and Johnson–Nyquist noise (a.k.a. thermal noise), which dominates at higher frequencies. The opamp's input and feedback path also have parasitic capacitance that modify and shape the noise.^[10]

Thermal noise

Fig. 6. Simple TIA with the feedback resistor modeled as noiseless resistance in parallel with a noise current source.

Because the opamp's inverting input is a virtual ground, the output-referred thermal voltage noise is simply the feedback resistor's thermal voltage noise. Over a particular bandwidth of ${\displaystyle \Delta f}$, this has a root mean square (RMS) amplitude that increases with the square root of the resistor's temperature ${\displaystyle T}$ and resistance ${\displaystyle R_{\text{f}}}$:

${\displaystyle {\sqrt {\overline {v_{\rm {n,out}}^{2}}}}={\sqrt {\overline {v_{\text{n}}^{2}}}}={\sqrt {4k_{\text{B}}TR_{\text{f}}\Delta f}},}$

where ${\displaystyle k_{\rm {B}}}$ is the Boltzmann constant.

The resistor can also be modeled as a noiseless resistance of ${\displaystyle R_{\text{f}}}$ in parallel with a thermal noise current source (Fig. 6). Because of Kirchhoff's current law at the opamp's inverting input, this thermal noise current is added with the input current as it flows into the resistance ${\displaystyle R_{\text{f}}}$. Thus, the input-referred thermal noise is identical to the thermal noise current, which has an RMS value of:

${\displaystyle {\sqrt {\overline {i_{\rm {n,in}}^{2}}}}={\sqrt {\overline {i_{\rm {n}}^{2}}}}={\sqrt {\frac {4k_{\text{B}}T\Delta f}{R_{\text{f}}}}}}$.

This input-referred thermal noise decreases with the reciprocal square-root of the resistance, even though the output-referred thermal noise grows with the square-root of the resistance. This is because the transimpedance of the amplifier instead grows linearly with the resistance. While this result suggests that a large feedback resistor is desirable for noise performance, a larger feedback resistance also increases the output voltage swing, and consequently a higher gain from the operational amplifier is needed, demanding an operational amplifier with a high gain-bandwidth product. The feedback resistance and therefore the sensitivity are thus limited by the required operating frequency of the transimpedance amplifier.

Discrete TIA design

It is also possible to construct a transimpedance amplifier with discrete components using a field effect transistor for the gain element. This has been done where a very low noise figure was required.^[11]

See also

• Operational transconductance amplifier – converts differential voltage into current
• Optical communication
• PIN diode

Sources

• Graeme, J.G. (1996). Photodiode Amplifiers: OP AMP Solutions. Gain technology. McGraw-Hill Education. ISBN 978-0-07-024247-0. Retrieved 12 November 2020.