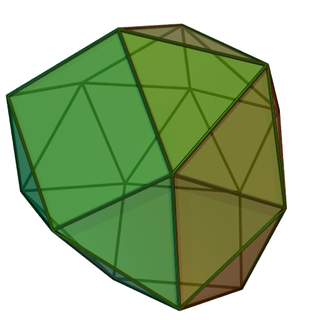
Disphenocingulum

In geometry, the disphenocingulum is a Johnson solid with 20 equilateral triangles and 4 squares as its faces.

Disphenocingulum
Type	Johnson J89 – J90 – J91
Faces	20 triangles 4 squares
Edges	38
Vertices	16
Vertex configuration	4(32.42) 4(35) 8(34.4)
Symmetry group	D2d
Properties	convex, elementary
Net

3D model of a disphenocingulum

Properties

The disphenocingulum is named by Johnson (1966). The prefix dispheno- refers to two wedgelike complexes, each formed by two adjacent lunes—a figure of two equilateral triangles at the opposite sides of a square. The suffix -cingulum, literally 'belt', refers to a band of 12 triangles joining the two wedges.^[1] The resulting polyhedron has 20 equilateral triangles and 4 squares, making 24 faces.^[2]. All of the faces are regular, categorizing the disphenocingulum as a Johnson solid—a convex polyhedron in which all of its faces are regular polygon—enumerated as 90th Johnson solid ${\displaystyle J_{90}}$.^[3]. It is an elementary polyhedron, meaning that it cannot be separated by a plane into two small regular-faced polyhedra.^[4]

The surface area of a disphenocingulum with edge length ${\displaystyle a}$ can be determined by adding all of its faces, the area of 20 equilateral triangles and 4 squares ${\displaystyle (4+5{\sqrt {3}})a^{2}\approx 12.6603a^{2}}$, and its volume is ${\displaystyle 3.7776a^{3}}$.^[2]

Cartesian coordinates

Let ${\displaystyle a\approx 0.76713}$ be the second smallest positive root of the polynomial $${\displaystyle {\begin{aligned}&256x^{12}-512x^{11}-1664x^{10}+3712x^{9}+1552x^{8}-6592x^{7}\\&\quad {}+1248x^{6}+4352x^{5}-2024x^{4}-944x^{3}+672x^{2}-24x-23\end{aligned}}}$$ and ${\displaystyle h={\sqrt {2+8a-8a^{2}}}}$ and ${\displaystyle c={\sqrt {1-a^{2}}}}$. Then, the Cartesian coordinates of a disphenocingulum with edge length 2 are given by the union of the orbits of the points $${\displaystyle \left(1,2a,{\frac {h}{2}}\right),\ \left(1,0,2c+{\frac {h}{2}}\right),\ \left(1+{\frac {\sqrt {3-4a^{2}}}{c}},0,2c-{\frac {1}{c}}+{\frac {h}{2}}\right)}$$ under the action of the group generated by reflections about the xz-plane and the yz-plane.^[5]