Drag crisis

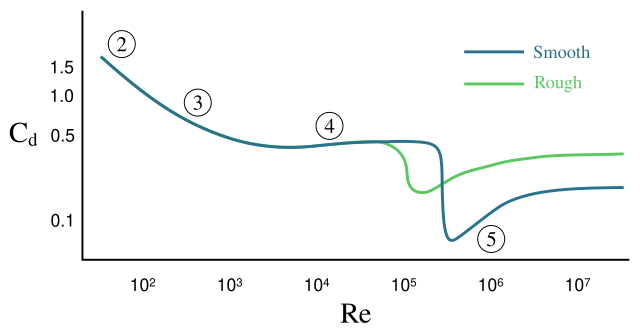
In fluid dynamics, the drag crisis (also known as the Eiffel paradox^[1]) is a phenomenon in which drag coefficient drops off suddenly as Reynolds number increases. This has been well studied for round bodies like spheres and cylinders. The drag coefficient of a sphere will change rapidly from about 0.5 to 0.2 at a Reynolds number in the range of 300000. This corresponds to the point where the flow pattern changes, leaving a narrower turbulent wake. The behavior is highly dependent on small differences in the condition of the surface of the sphere.

The drag coefficient of a sphere drops at high Reynolds number (number 5 on the graph). The effect occurs at lower Reynolds numbers when the ball is rough (such as a golf ball with dimples) than when it is smooth (such as a table tennis ball).

History

The drag crisis was observed in 1905^{[citation needed]} by Nikolay Zhukovsky, who guessed that this paradox can be explained by the detachment of streamlines at different points of the sphere at different velocities.^[2]

Later the paradox was independently discovered in experiments by Gustave Eiffel^[3] and Charles Maurain.^[4] Upon Eiffel's retirement, he built the first wind tunnel in a lab located at the base of the Eiffel Tower, to investigate wind loads on structures and early aircraft. In a series of tests he found that the force loading experienced an abrupt decline at a critical Reynolds number.

The paradox was explained from boundary-layer theory by German fluid dynamicist Ludwig Prandtl.^[5]

Explanation

The drag crisis is associated with a transition from laminar to turbulent boundary layer flow adjacent to the object. For cylindrical structures, this transition is associated with a transition from well-organized vortex shedding to randomized shedding behavior for super-critical Reynolds numbers, eventually returning to well-organized shedding at a higher Reynolds number with a return to elevated drag force coefficients.

The super-critical behavior can be described semi-empirically using statistical means or by sophisticated computational fluid dynamics software (CFD) that takes into account the fluid-structure interaction for the given fluid conditions using Large Eddy Simulation (LES) that includes the dynamic displacements of the structure (DLES) [11]. These calculations also demonstrate the importance of the blockage ratio present for intrusive fittings in pipe flow and wind-tunnel tests.

The critical Reynolds number is a function of turbulence intensity, upstream velocity profile, and wall-effects (velocity gradients). The semi-empirical descriptions of the drag crisis are often described in terms of a Strouhal bandwidth and the vortex shedding is described by broad-band spectral content.