Equal detour point

In Euclidean geometry, the equal detour point is a triangle center denoted by X(176) in Clark Kimberling's Encyclopedia of Triangle Centers. It is characterized by the equal detour property: if one travels from any vertex of a triangle △ABC to another by taking a detour through some inner point P, then the additional distance traveled is constant. This means the following equation has to hold:^[1]

${\displaystyle {\begin{aligned}&{\overline {AP}}+{\overline {PC}}-{\overline {AC}}\\[3mu]={}&{\overline {AP}}+{\overline {PB}}-{\overline {AB}}\\[3mu]={}&{\overline {BP}}+{\overline {PC}}-{\overline {BC}}.\end{aligned}}}$

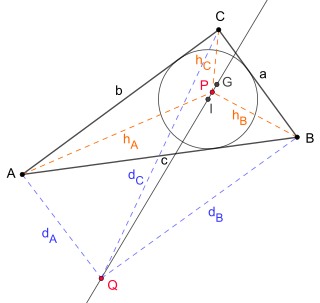
  Triangle △ABC (side lengths a, b, c)

  Incircle (centered at incenter I)

  Isoperimetric lines d_A, d_B, d_C (concur at isoperimetric point Q)

  Detours h_A, h_B, h_C (concur at equal detour point P):

$${\displaystyle {\begin{aligned}&h_{A}+h_{C}-b\\={}&h_{A}+h_{B}-c\\={}&h_{B}+h_{C}-a\end{aligned}}}$$ I, Q, P and the Gergonne point G are collinear and form a harmonic range: $${\displaystyle {\frac {\overline {QI}}{\overline {PI}}}={\frac {\overline {QG}}{\overline {PG}}}}$$

The equal detour point is the only point with the equal detour property if and only if the following inequality holds for the angles α, β, γ of △ABC:^[2]

${\displaystyle \tan {\tfrac {1}{2}}\alpha +\tan {\tfrac {1}{2}}\beta +\tan {\tfrac {1}{2}}\gamma \leq 2}$

If the inequality does not hold, then the isoperimetric point possesses the equal detour property as well.

The equal detour point, isoperimetric point, the incenter and the Gergonne point of a triangle are collinear, that is all four points lie on a common line. Furthermore, they form a harmonic range (see graphic on the right).^[3]

The equal detour point is the center of the inner Soddy circle of a triangle and the additional distance travelled by the detour is equal to the diameter of the inner Soddy Circle.^[3]

The barycentric coordinates of the equal detour point are^[3]

${\displaystyle \left(a+{\frac {\Delta }{s-a}}:b+{\frac {\Delta }{s-b}}:c+{\frac {\Delta }{s-c}}\right).}$

and the trilinear coordinates are:^[1] $${\displaystyle 1+{\frac {\cos {\tfrac {1}{2}}\beta \,\cos {\tfrac {1}{2}}\gamma }{\cos {\tfrac {1}{2}}\alpha }}\$$ :\ 1+{\frac {\cos {\tfrac {1}{2}}\gamma \,\cos {\tfrac {1}{2}}\alpha }{\cos {\tfrac {1}{2}}\beta }}\ :\ 1+{\frac {\cos {\tfrac {1}{2}}\alpha \,\cos {\tfrac {1}{2}}\beta }{\cos {\tfrac {1}{2}}\gamma }}}