Top Qs
Timeline
Chat
Perspective
F-distribution
Continuous probability distribution From Wikipedia, the free encyclopedia
Remove ads
In probability theory and statistics, the F-distribution or F-ratio, also known as Snedecor's F distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor), is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other F-tests.[2][3][4][5]
Remove ads
Definitions
Summarize
Perspective
The F-distribution with d1 and d2 degrees of freedom is the distribution of
where and are independent random variables with chi-square distributions with respective degrees of freedom and .
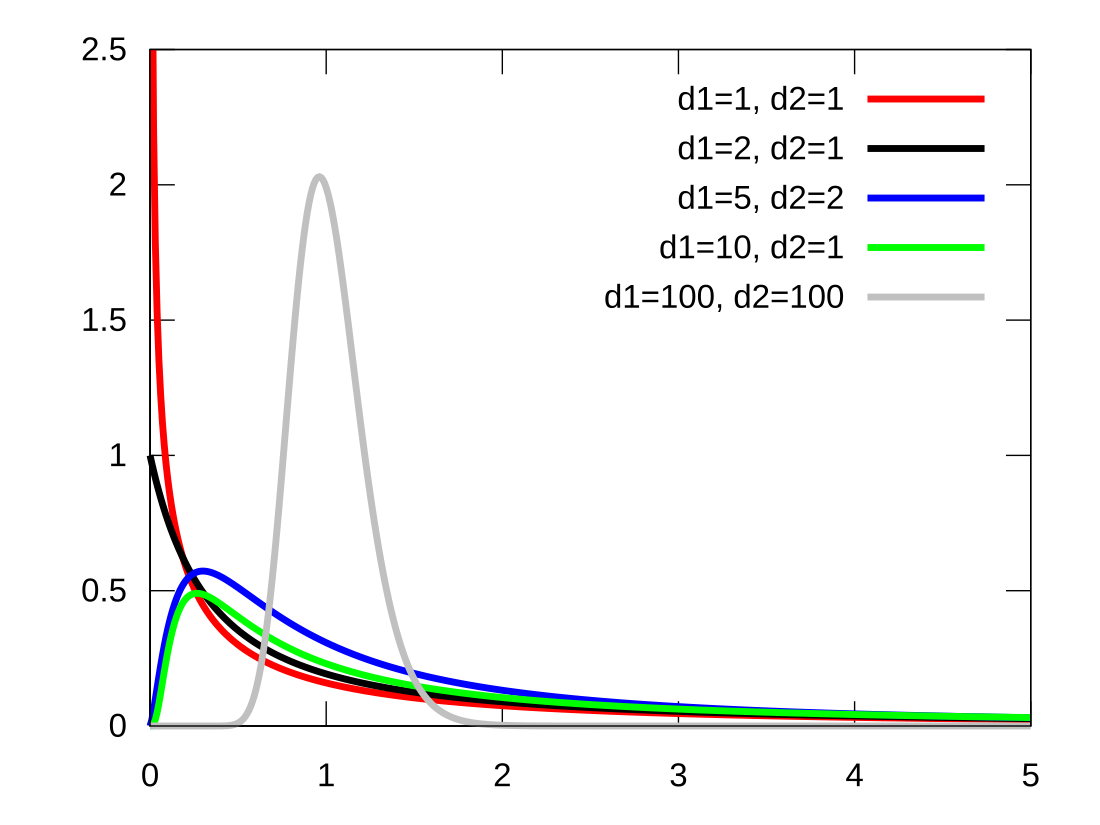
It can be shown to follow that the probability density function (pdf) for X is given by
for real x > 0. Here is the beta function. In many applications, the parameters d1 and d2 are positive integers, but the distribution is well-defined for positive real values of these parameters.
The cumulative distribution function is
where I is the regularized incomplete beta function.
Remove ads
Properties
Summarize
Perspective
The expectation, variance, and other details about the F(d1, d2) are given in the sidebox; for d2 > 8, the excess kurtosis is
The k-th moment of an F(d1, d2) distribution exists and is finite only when 2k < d2 and it is equal to[6]
The F-distribution is a particular parametrization of the beta prime distribution, which is also called the beta distribution of the second kind.
The characteristic function is listed incorrectly in many standard references (e.g.,[3]). The correct expression [7] is
where U(a, b, z) is the confluent hypergeometric function of the second kind.
Remove ads
Related distributions
Summarize
Perspective
Relation to the chi-squared distribution
In instances where the F-distribution is used, for example in the analysis of variance, independence of and (defined above) might be demonstrated by applying Cochran's theorem.
Equivalently, since the chi-squared distribution is the sum of squares of independent standard normal random variables, the random variable of the F-distribution may also be written
where and , is the sum of squares of random variables from normal distribution and is the sum of squares of random variables from normal distribution .
In a frequentist context, a scaled F-distribution therefore gives the probability , with the F-distribution itself, without any scaling, applying where is being taken equal to . This is the context in which the F-distribution most generally appears in F-tests: where the null hypothesis is that two independent normal variances are equal, and the observed sums of some appropriately selected squares are then examined to see whether their ratio is significantly incompatible with this null hypothesis.
The quantity has the same distribution in Bayesian statistics, if an uninformative rescaling-invariant Jeffreys prior is taken for the prior probabilities of and .[8] In this context, a scaled F-distribution thus gives the posterior probability , where the observed sums and are now taken as known.
In general
- If and (Chi squared distribution) are independent, then
- If (Gamma distribution) are independent, then
- If (Beta distribution) then
- Equivalently, if , then .
- If , then has a beta prime distribution: .
- If then has the chi-squared distribution
- is equivalent to the scaled Hotelling's T-squared distribution .
- If then .
- If — Student's t-distribution — then:
- F-distribution is a special case of type 6 Pearson distribution
- If and are independent, with Laplace(μ, b) then
- If then (Fisher's z-distribution)
- The noncentral F-distribution simplifies to the F-distribution if .
- The doubly noncentral F-distribution simplifies to the F-distribution if
- If is the quantile p for and is the quantile for , then
- F-distribution is an instance of ratio distributions
- W-distribution[9] is a unique parametrization of F-distribution.
Remove ads
See also
- Beta prime distribution
- Chi-square distribution
- Chow test
- Gamma distribution
- Hotelling's T-squared distribution
- Wilks' lambda distribution
- Wishart distribution
- Modified half-normal distribution[10] with the pdf on is given as , where denotes the Fox–Wright Psi function.
Remove ads
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

















![{\displaystyle {\begin{aligned}f(x;d_{1},d_{2})&={\frac {\sqrt {\frac {(d_{1}x)^{d_{1}}\,\,d_{2}^{d_{2}}}{(d_{1}x+d_{2})^{d_{1}+d_{2}}}}}{x\operatorname {B} \left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\\[5pt]&={\frac {1}{\operatorname {B} \left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\left({\frac {d_{1}}{d_{2}}}\right)^{\frac {d_{1}}{2}}x^{{\frac {d_{1}}{2}}-1}\left(1+{\frac {d_{1}}{d_{2}}}\,x\right)^{-{\frac {d_{1}+d_{2}}{2}}}\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bc2f8be5060a08b5c1fcb90902d5a3e09fb622f4)























































