Variance

This article is about the mathematical concept. For other uses, see Variance (disambiguation).

In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by ${\displaystyle \sigma ^{2}}$, ${\displaystyle s^{2}}$, ${\displaystyle \operatorname {Var} (X)}$, ${\displaystyle V(X)}$, or ${\displaystyle \mathbb {V} (X)}$.^[1]

Example of samples from two populations with the same mean but different variances. The red population has mean 100 and variance 100 (SD=10) while the blue population has mean 100 and variance 2500 (SD=50) where SD stands for Standard Deviation.

An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard deviation is more commonly reported as a measure of dispersion once the calculation is finished. Another disadvantage is that the variance is not finite for many distributions.

There are two distinct concepts that are both called "variance". One, as discussed above, is part of a theoretical probability distribution and is defined by an equation. The other variance is a characteristic of a set of observations. When variance is calculated from observations, those observations are typically measured from a real-world system. If all possible observations of the system are present, then the calculated variance is called the population variance. Normally, however, only a subset is available, and the variance calculated from this is called the sample variance. The variance calculated from a sample is considered an estimate of the full population variance. There are multiple ways to calculate an estimate of the population variance, as discussed in the section below.

The two kinds of variance are closely related. To see how, consider that a theoretical probability distribution can be used as a generator of hypothetical observations. If an infinite number of observations are generated using a distribution, then the sample variance calculated from that infinite set will match the value calculated using the distribution's equation for variance. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling.

Geometric visualisation of the variance of an arbitrary distribution (2, 4, 4, 4, 5, 5, 7, 9):

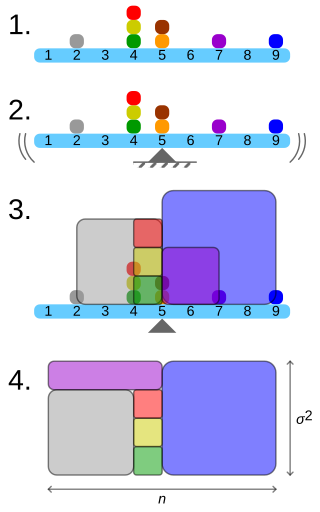
1. A frequency distribution is constructed.
2. The centroid of the distribution gives its mean.
3. A square with sides equal to the difference of each value from the mean is formed for each value.
4. Arranging the squares into a rectangle with one side equal to the number of values, n, results in the other side being the distribution's variance, σ².

The variance of a random variable ${\displaystyle X}$ is the expected value of the squared deviation from the mean of ${\displaystyle X}$, ${\displaystyle \mu =\operatorname {E} [X]}$:

${\displaystyle \operatorname {Var} (X)=\operatorname {E} \left[(X-\mu )^{2}\right].}$

This definition encompasses random variables that are generated by processes that are discrete, continuous, neither, or mixed. The variance can also be thought of as the covariance of a random variable with itself:

${\displaystyle \operatorname {Var} (X)=\operatorname {Cov} (X,X).}$

The variance is also equivalent to the second cumulant of a probability distribution that generates ${\displaystyle X}$. The variance is typically designated as ${\displaystyle \operatorname {Var} (X)}$, or sometimes as ${\displaystyle V(X)}$ or ${\displaystyle \mathbb {V} (X)}$, or symbolically as ${\displaystyle \sigma _{X}^{2}}$ or simply ${\displaystyle \sigma ^{2}}$ (pronounced "sigma squared"). The expression for the variance can be expanded as follows:

${\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left[(X-\operatorname {E} [X])^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}-2X\operatorname {E} [X]+\operatorname {E} [X]^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}\right]-2\operatorname {E} [X]\operatorname {E} [X]+\operatorname {E} [X]^{2}\\[4pt]&=\operatorname {E} \left[X^{2}\right]-2\operatorname {E} [X]^{2}+\operatorname {E} [X]^{2}\\[4pt]&=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}\end{aligned}}}$

In other words, the variance of X is equal to the mean of the square of X minus the square of the mean of X. This equation should not be used for computations using floating point arithmetic, because it suffers from catastrophic cancellation if the two components of the equation are similar in magnitude. For other numerically stable alternatives, see Algorithms for calculating variance.

Discrete random variable

If the generator of random variable ${\displaystyle X}$ is discrete with probability mass function ${\displaystyle x_{1}\mapsto p_{1},x_{2}\mapsto p_{2},\ldots ,x_{n}\mapsto p_{n}}$, then

${\displaystyle \operatorname {Var} (X)=\sum _{i=1}^{n}p_{i}\cdot (x_{i}-\mu )^{2},}$

where ${\displaystyle \mu }$ is the expected value. That is,

${\displaystyle \mu =\sum _{i=1}^{n}p_{i}x_{i}.}$

(When such a discrete weighted variance is specified by weights whose sum is not 1, then one divides by the sum of the weights.)

The variance of a collection of ${\displaystyle n}$ equally likely values can be written as

${\displaystyle \operatorname {Var} (X)={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}}$

where ${\displaystyle \mu }$ is the average value. That is,

${\displaystyle \mu ={\frac {1}{n}}\sum _{i=1}^{n}x_{i}.}$

The variance of a set of ${\displaystyle n}$ equally likely values can be equivalently expressed, without directly referring to the mean, in terms of squared deviations of all pairwise squared distances of points from each other:^[2]

${\displaystyle \operatorname {Var} (X)={\frac {1}{n^{2}}}\sum _{i=1}^{n}\sum _{j=1}^{n}{\frac {1}{2}}(x_{i}-x_{j})^{2}={\frac {1}{n^{2}}}\sum _{i}\sum _{j>i}(x_{i}-x_{j})^{2}.}$

Absolutely continuous random variable

If the random variable ${\displaystyle X}$ has a probability density function ${\displaystyle f(x)}$, and ${\displaystyle F(x)}$ is the corresponding cumulative distribution function, then

${\displaystyle {\begin{aligned}\operatorname {Var} (X)=\sigma ^{2}&=\int _{\mathbb {R} }(x-\mu )^{2}f(x)\,dx\\[4pt]&=\int _{\mathbb {R} }x^{2}f(x)\,dx-2\mu \int _{\mathbb {R} }xf(x)\,dx+\mu ^{2}\int _{\mathbb {R} }f(x)\,dx\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-2\mu \int _{\mathbb {R} }x\,dF(x)+\mu ^{2}\int _{\mathbb {R} }\,dF(x)\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-2\mu \cdot \mu +\mu ^{2}\cdot 1\\[4pt]&=\int _{\mathbb {R} }x^{2}\,dF(x)-\mu ^{2},\end{aligned}}}$

or equivalently,

${\displaystyle \operatorname {Var} (X)=\int _{\mathbb {R} }x^{2}f(x)\,dx-\mu ^{2},}$

where ${\displaystyle \mu }$ is the expected value of ${\displaystyle X}$ given by

${\displaystyle \mu =\int _{\mathbb {R} }xf(x)\,dx=\int _{\mathbb {R} }x\,dF(x).}$

In these formulas, the integrals with respect to ${\displaystyle dx}$ and ${\displaystyle dF(x)}$ are Lebesgue and Lebesgue–Stieltjes integrals, respectively.

If the function ${\displaystyle x^{2}f(x)}$ is Riemann-integrable on every finite interval ${\displaystyle [a,b]\subset \mathbb {R} ,}$ then

${\displaystyle \operatorname {Var} (X)=\int _{-\infty }^{+\infty }x^{2}f(x)\,dx-\mu ^{2},}$

where the integral is an improper Riemann integral.

Exponential distribution

The exponential distribution with parameter λ is a continuous distribution whose probability density function is given by

${\displaystyle f(x)=\lambda e^{-\lambda x}}$

on the interval [0, ∞). Its mean can be shown to be

${\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }x\lambda e^{-\lambda x}\,dx={\frac {1}{\lambda }}.}$

Using integration by parts and making use of the expected value already calculated, we have:

${\displaystyle {\begin{aligned}\operatorname {E} \left[X^{2}\right]&=\int _{0}^{\infty }x^{2}\lambda e^{-\lambda x}\,dx\\&=\left[-x^{2}e^{-\lambda x}\right]_{0}^{\infty }+\int _{0}^{\infty }2xe^{-\lambda x}\,dx\\&=0+{\frac {2}{\lambda }}\operatorname {E} [X]\\&={\frac {2}{\lambda ^{2}}}.\end{aligned}}}$

Thus, the variance of X is given by

${\displaystyle \operatorname {Var} (X)=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}={\frac {2}{\lambda ^{2}}}-\left({\frac {1}{\lambda }}\right)^{2}={\frac {1}{\lambda ^{2}}}.}$

Fair die

A fair six-sided die can be modeled as a discrete random variable, X, with outcomes 1 through 6, each with equal probability 1/6. The expected value of X is ${\displaystyle (1+2+3+4+5+6)/6=7/2.}$ Therefore, the variance of X is

${\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\sum _{i=1}^{6}{\frac {1}{6}}\left(i-{\frac {7}{2}}\right)^{2}\\[5pt]&={\frac {1}{6}}\left((-5/2)^{2}+(-3/2)^{2}+(-1/2)^{2}+(1/2)^{2}+(3/2)^{2}+(5/2)^{2}\right)\\[5pt]&={\frac {35}{12}}\approx 2.92.\end{aligned}}}$

The general formula for the variance of the outcome, X, of an n-sided die is

${\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left(X^{2}\right)-(\operatorname {E} (X))^{2}\\[5pt]&={\frac {1}{n}}\sum _{i=1}^{n}i^{2}-\left({\frac {1}{n}}\sum _{i=1}^{n}i\right)^{2}\\[5pt]&={\frac {(n+1)(2n+1)}{6}}-\left({\frac {n+1}{2}}\right)^{2}\\[4pt]&={\frac {n^{2}-1}{12}}.\end{aligned}}}$

Commonly used probability distributions

The following table lists the variance for some commonly used probability distributions.

Name of the probability distribution	Probability distribution function	Mean	Variance
Binomial distribution	${\displaystyle \Pr \,(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}}$	${\displaystyle np}$	${\displaystyle np(1-p)}$
Geometric distribution	${\displaystyle \Pr \,(X=k)=(1-p)^{k-1}p}$	${\displaystyle {\frac {1}{p}}}$	${\displaystyle {\frac {(1-p)}{p^{2}}}}$
Normal distribution	${\displaystyle f\left(x\mid \mu ,\sigma ^{2}\right)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}$	${\displaystyle \mu }$	${\displaystyle \sigma ^{2}}$
Uniform distribution (continuous)	${\displaystyle f(x\mid a,b)={\begin{cases}{\frac {1}{b-a}}&{\text{for }}a\leq x\leq b,\\[3pt]0&{\text{for }}x<a{\text{ or }}x>b\end{cases}}}$	${\displaystyle {\frac {a+b}{2}}}$	${\displaystyle {\frac {(b-a)^{2}}{12}}}$
Exponential distribution	${\displaystyle f(x\mid \lambda )=\lambda e^{-\lambda x}}$	${\displaystyle {\frac {1}{\lambda }}}$	${\displaystyle {\frac {1}{\lambda ^{2}}}}$
Poisson distribution	${\displaystyle f(k\mid \lambda )={\frac {e^{-\lambda }\lambda ^{k}}{k!}}}$	${\displaystyle \lambda }$	${\displaystyle \lambda }$

Basic properties

Variance is non-negative because the squares are positive or zero:

${\displaystyle \operatorname {Var} (X)\geq 0.}$

The variance of a constant is zero.

${\displaystyle \operatorname {Var} (a)=0.}$

Conversely, if the variance of a random variable is 0, then it is almost surely a constant. That is, it always has the same value:

${\displaystyle \operatorname {Var} (X)=0\iff \exists a:P(X=a)=1.}$

Issues of finiteness

If a distribution does not have a finite expected value, as is the case for the Cauchy distribution, then the variance cannot be finite either. However, some distributions may not have a finite variance, despite their expected value being finite. An example is a Pareto distribution whose index ${\displaystyle k}$ satisfies ${\displaystyle 1<k\leq 2.}$

Decomposition

The general formula for variance decomposition or the law of total variance is: If ${\displaystyle X}$ and ${\displaystyle Y}$ are two random variables, and the variance of ${\displaystyle X}$ exists, then

${\displaystyle \operatorname {Var} [X]=\operatorname {E} (\operatorname {Var} [X\mid Y])+\operatorname {Var} (\operatorname {E} [X\mid Y]).}$

The conditional expectation ${\displaystyle \operatorname {E} (X\mid Y)}$ of ${\displaystyle X}$ given ${\displaystyle Y}$, and the conditional variance ${\displaystyle \operatorname {Var} (X\mid Y)}$ may be understood as follows. Given any particular value y of the random variable Y, there is a conditional expectation ${\displaystyle \operatorname {E} (X\mid Y=y)}$ given the event Y = y. This quantity depends on the particular value y; it is a function ${\displaystyle g(y)=\operatorname {E} (X\mid Y=y)}$. That same function evaluated at the random variable Y is the conditional expectation ${\displaystyle \operatorname {E} (X\mid Y)=g(Y).}$

In particular, if ${\displaystyle Y}$ is a discrete random variable assuming possible values ${\displaystyle y_{1},y_{2},y_{3}\ldots }$ with corresponding probabilities ${\displaystyle p_{1},p_{2},p_{3}\ldots ,}$, then in the formula for total variance, the first term on the right-hand side becomes

${\displaystyle \operatorname {E} (\operatorname {Var} [X\mid Y])=\sum _{i}p_{i}\sigma _{i}^{2},}$

where ${\displaystyle \sigma _{i}^{2}=\operatorname {Var} [X\mid Y=y_{i}]}$. Similarly, the second term on the right-hand side becomes

${\displaystyle \operatorname {Var} (\operatorname {E} [X\mid Y])=\sum _{i}p_{i}\mu _{i}^{2}-\left(\sum _{i}p_{i}\mu _{i}\right)^{2}=\sum _{i}p_{i}\mu _{i}^{2}-\mu ^{2},}$

where ${\displaystyle \mu _{i}=\operatorname {E} [X\mid Y=y_{i}]}$ and ${\displaystyle \mu =\sum _{i}p_{i}\mu _{i}}$. Thus the total variance is given by

${\displaystyle \operatorname {Var} [X]=\sum _{i}p_{i}\sigma _{i}^{2}+\left(\sum _{i}p_{i}\mu _{i}^{2}-\mu ^{2}\right).}$

A similar formula is applied in analysis of variance, where the corresponding formula is

${\displaystyle {\mathit {MS}}_{\text{total}}={\mathit {MS}}_{\text{between}}+{\mathit {MS}}_{\text{within}};}$

here ${\displaystyle {\mathit {MS}}}$ refers to the Mean of the Squares. In linear regression analysis the corresponding formula is

${\displaystyle {\mathit{M}\mathit{S}}_{}}$