Folium of Descartes

In geometry, the folium of Descartes (from Latin folium 'leaf'; named for René Descartes) is an algebraic curve defined by the implicit equation

The folium of Descartes (green) with asymptote (blue), when ${\textstyle a=1}$

${\displaystyle x^{3}+y^{3}-3a\cdot xy=0.}$

^[1]${\displaystyle dy/dx=(x^{2}-ay)/(ax-y^{2}),\,dx/dy=(ax-y^{2})/(x^{2}-ay).}$

History

The curve was first proposed and studied by René Descartes in 1638.^[2] Its claim to fame lies in an incident in the development of calculus. Descartes challenged Pierre de Fermat to find the tangent line to the curve at an arbitrary point, since Fermat had recently discovered a method for finding tangent lines. Fermat solved the problem easily, something Descartes was unable to do.^[3] Since the invention of calculus, the slope of the tangent line can be found easily using implicit differentiation.^[4] Mayor Johan(nes) Hudde's second letter on maxima and minima (1658) mentions his calculation of the maximum width of the closed loop, part of Mathematical Exercitions, 5 books (1656/57 Leyden) p. 498, by Frans van Schooten Jnr.

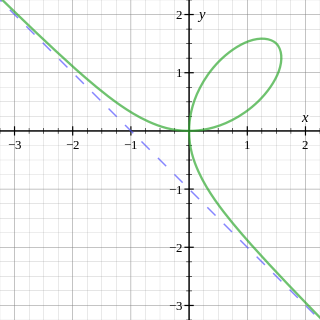
Graphing the curve

Folium of Descartes in polar coordinates r-φ: ${\textstyle r(\phi )/a,\,a=1}$

The folium of Descartes can be expressed in polar coordinates as$${\displaystyle r={\frac {3a\sin \theta \cos \theta }{\sin ^{3}\theta +\cos ^{3}\theta }},}$$which is plotted on the left. This is equivalent to^[5]

${\displaystyle r={\frac {3a\sec \theta \tan \theta }{1+\tan ^{3}\theta }}.}$

Another technique is to write ${\displaystyle y=px}$ and solve for ${\displaystyle x}$ and ${\displaystyle y}$ in terms of ${\displaystyle p}$. This yields the rational parametric equations:^[6]

${\displaystyle x={{3ap} \over {1+p^{3}}},\,y={{3ap^{2}} \over {1+p^{3}}}.}$

We can see that the parameter is related to the position on the curve as follows:

• ${\displaystyle p<-1}$ corresponds to ${\displaystyle x>0}$, ${\displaystyle y<0}$: the right, lower, "wing".
• ${\displaystyle -1<p<0}$ corresponds to ${\displaystyle x<0}$, ${\displaystyle y>0}$: the left, upper "wing".
• ${\displaystyle p>0}$ corresponds to ${\displaystyle x>0}$, ${\displaystyle y>0}$: the loop of the curve.

Another way of plotting the function can be derived from symmetry over ${\displaystyle y=x}$. The symmetry can be seen directly from its equation (x and y can be interchanged). By applying rotation of 45° clockwise for example, one can plot the function symmetric over rotated x axis.

This operation is equivalent to a substitution:$${\displaystyle x={{u+v} \over {\sqrt {2}}},\,y={{u-v} \over {\sqrt {2}}}}$$and yields$${\displaystyle v=\pm u{\sqrt {\frac {3a{\sqrt {2}}-2u}{6u+3a{\sqrt {2}}}}}\,,\,u<3a/{\sqrt {2}}.}$$Plotting in the Cartesian system of ${\displaystyle (u,v)}$ gives the folium rotated by 45° and therefore symmetric by ${\displaystyle u}$-axis.

Properties

It forms a loop in the first quadrant with a double point at the origin and has asymptote$${\displaystyle x+y=-a\,.}$$It is symmetrical about the line ${\displaystyle y=x}$. As such, the curve and this line intersect at the origin and at the point ${\textstyle (3a/2,3a/2).}$

Implicit differentiation gives the formula for the slope of the tangent line to this curve to be^[4]

${\displaystyle {\frac {dy}{dx}}={\frac {ay-x^{2}}{y^{2}-ax}}\,,}$ with poles ${\textstyle x=y^{2}/a}$ and value 0 or ±∞ at origin (0,0).

Using either one of the polar representations above, the area of the interior of the loop is found to be ${\textstyle 1{\frac {1}{2}}a\cdot a.}$ Moreover, the area between the "wings" of the curve and its slanted asymptote is also ${\textstyle 3a^{2}/2.}$^[2]

Relationship to the trisectrix of Maclaurin

Trisectrix of Maclaurin: top angle is ⁠2/3⁠ φ. Length ⁠1+1/2⁠ a on hor. axis, O to turning point.

The folium of Descartes is related to the trisectrix of Maclaurin by affine transformation. To see this, start with the equation$${\displaystyle x^{3}+y^{3}=3a\cdot xy\,,}$$and change variables to find the equation in a coordinate system rotated 45 degrees. This amounts to setting

$${\displaystyle x={{X+Y} \over {\sqrt {2}}},y={{X-Y} \over {\sqrt {2}}}.}$$In the ${\displaystyle X,Y}$ plane the equation is$${\displaystyle 2X(X^{2}+3Y^{2})=3{\sqrt {2}}a(X^{2}-Y^{2}).}$$

If we stretch the curve in the ${\displaystyle Y}$ direction by a factor of ${\displaystyle {\sqrt {3}}}$ this becomes$${\displaystyle 2X(X^{2}+Y^{2})=a{\sqrt {2}}(3X^{2}-Y^{2}),}$$which is the equation of the trisectrix of Maclaurin.