Hinge theorem

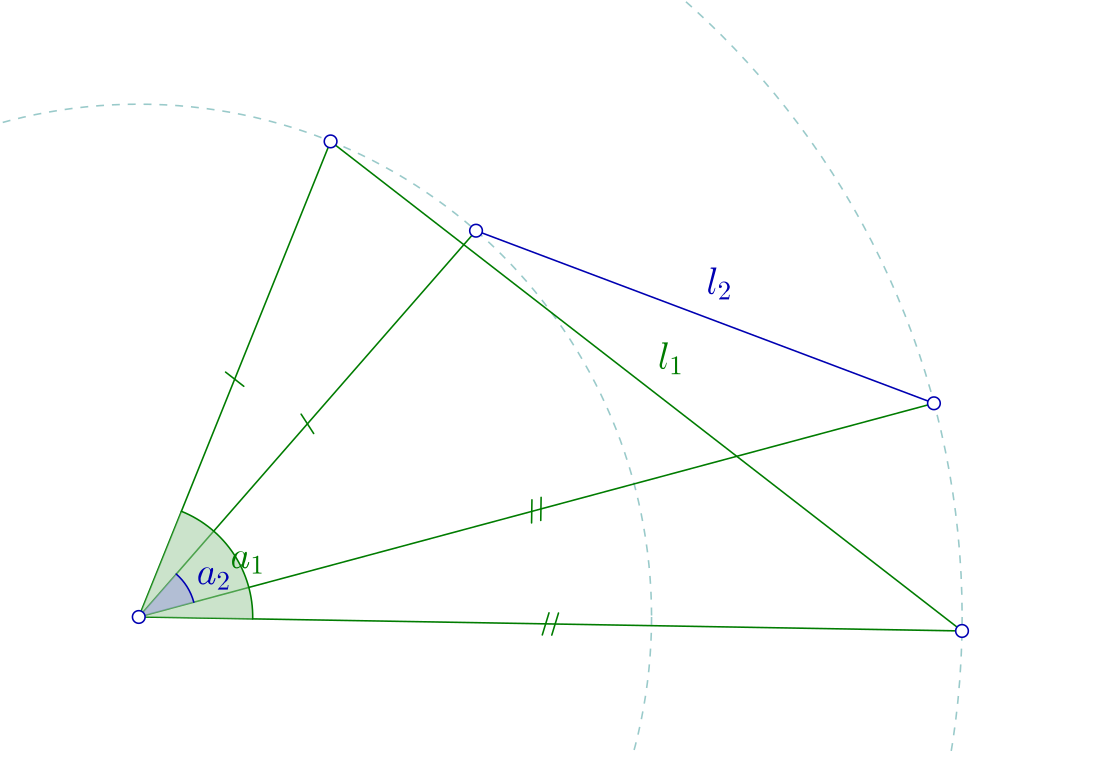
In geometry, the hinge theorem (sometimes called the open mouth theorem) states that if two sides of one triangle are congruent to two sides of another triangle, and the included angle of the first is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second triangle.^[1] This theorem is given as Proposition 24 in Book I of Euclid's Elements.

Proof from the law of cosines

The theorem is an immediate corollary of the law of cosines.^[2] For two triangles with sides ${\displaystyle \{a,b,c\}}$ and ${\displaystyle \{a,b,{\hat {c}}\}}$ with angles ${\displaystyle \gamma }$ and ${\displaystyle {\hat {\gamma }}}$ opposite the respective sides ${\displaystyle c}$ and ${\displaystyle {\hat {c}}}$, the law of cosines states:

$${\displaystyle {\begin{aligned}c^{2}&=a^{2}+b^{2}-2ab\cos \gamma ,\\{\hat {c}}^{2}&=a^{2}+b^{2}-2ab\cos {\hat {\gamma }}.\end{aligned}}}$$

The cosine function is monotonically decreasing for angles between ${\displaystyle 0}$ and ${\displaystyle \pi }$ radians, so ${\displaystyle {\hat {\gamma }}>\gamma }$ implies ${\displaystyle {\hat {c}}>c}$ (and the converse as well).

Scope and generalizations

The hinge theorem holds in Euclidean spaces and more generally in simply connected non-positively curved space forms.

It can be also extended from plane Euclidean geometry to higher dimension Euclidean spaces (e.g., to tetrahedra and more generally to simplices), as has been done for orthocentric tetrahedra (i.e., tetrahedra in which altitudes are concurrent)^[2] and more generally for orthocentric simplices (i.e., simplices in which altitudes are concurrent).^[3]

Converse

The converse of the hinge theorem is also true: If the two sides of one triangle are congruent to two sides of another triangle, and the third side of the first triangle is greater than the third side of the second triangle, then the included angle of the first triangle is larger than the included angle of the second triangle.

In some textbooks, the theorem and its converse are written as the SAS Inequality Theorem and the AAS Inequality Theorem respectively.