Intersection

This article is about a broad mathematical concept. For the point where roads meet, see Intersection (road). For other uses, see Intersection (disambiguation).

In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, their intersection is the point at which they meet. More generally, in set theory, the intersection of sets is defined to be the set of elements which belong to all of them.

The intersection (red) of two disks (white and red with black boundaries).

The circle (black) intersects the line (purple) in two points (red). The disk (yellow) intersects the line in the line segment between the two red points.

The intersection of D and E is shown in grayish purple. The intersection of A with any of B, C, D, or E is the empty set.

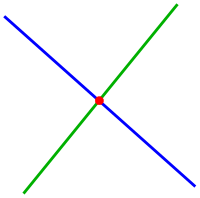
Intersections can be thought of either collectively or individually, see Intersection (geometry) for an example of the latter. The definition given above exemplifies the collective view, whereby the intersection operation always results in a well-defined and unique, although possibly empty, set of mathematical objects. In contrast, the individual view focuses on the separate members of this set. Given this view, intersections need not be unique, as shown by the two points of intersection between a circle and a line pictured. Similarly, (individual) intersections need not exist as between two parallel but distinct lines in Euclidean geometry.

Intersection is one of the basic concepts of geometry. An intersection can have various geometric shapes, but a point is the most common in a plane geometry. Incidence geometry defines an intersection (usually, of flats) as an object of lower dimension that is incident to each of the original objects. In this approach, an intersection can be sometimes undefined, such as for parallel lines. In both the cases the concept of intersection relies on logical conjunction. Algebraic geometry defines intersections in its own way with intersection theory.

In set theory

Considering a road to correspond to the set of all its locations, a road intersection (cyan) of two roads (green, blue) corresponds to the intersection of their sets.

Main article: Intersection (set theory)

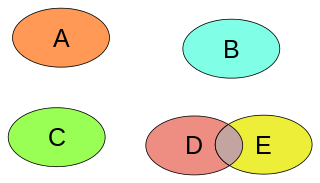
The intersection of two sets A and B is the set of elements which are in both A and B. Formally,

${\displaystyle A\cap B=\{x:x\in A{\text{ and }}x\in B\}}$.^[1]

For example, if ${\displaystyle A=\{1,3,5,7\}}$ and ${\displaystyle B=\{1,2,4,6\}}$, then ${\displaystyle A\cap B=\{1\}}$. A more elaborate example (involving infinite sets) is:

${\displaystyle A=\{x:{\text{ x is an even integer}}\}}$

${\displaystyle B=\{x:{\text{ x is an integer divisible by 3}}\}}$${\displaystyle {\text{ , then}}}$

${\displaystyle A\cap B=\{6,12,18,\dots \}}$

As another example, the number 5 is not contained in the intersection of the set of prime numbers {2, 3, 5, 7, 11, …} and the set of even numbers {2, 4, 6, 8, 10, …} , because although 5 is a prime number, it is not even.

Sets can have an empty intersection. For example, if ${\displaystyle A=\{Amy,\,Aaron,\,Arjun\}}$ and ${\displaystyle B=\{Barack,\,Bas,\,Betty\}}$, then ${\displaystyle A\cap B=\emptyset }$. Such sets are called disjoint sets and may colloquially be said to have no intersection.

In geometry

This section is an excerpt from Intersection (geometry).[edit]

The red dot represents the point at which the two lines intersect.

In geometry, an intersection is a point, line, or curve common to two or more objects (such as lines, curves, planes, and surfaces). The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point (sometimes called a vertex) or does not exist (if the lines are parallel). Other types of geometric intersection include:

• Line–plane intersection
• Line–sphere intersection
• Intersection of a polyhedron with a line
• Line segment intersection
• Intersection curve

Determination of the intersection of flats – linear geometric objects embedded in a higher-dimensional space – is a simple task of linear algebra, namely the solution of a system of linear equations. In general the determination of an intersection leads to non-linear equations, which can be solved numerically, for example using Newton iteration. Intersection problems between a line and a conic section (circle, ellipse, parabola, etc.) or a quadric (sphere, cylinder, hyperboloid, etc.) lead to quadratic equations that can be easily solved. Intersections between quadrics lead to quartic equations that can be solved algebraically.

Notation

Intersection is denoted by the U+2229 ∩ INTERSECTION from Unicode Mathematical Operators.

The symbol U+2229 ∩ INTERSECTION was first used by Hermann Grassmann in Die Ausdehnungslehre von 1844 as general operation symbol, not specialized for intersection. From there, it was used by Giuseppe Peano (1858–1932) for intersection, in 1888 in Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann.^[2][3]

Peano also created the large symbols for general intersection and union of more than two classes in his 1908 book Formulario mathematico.^[4][5]

See also

• Constructive solid geometry, Boolean Intersection is one of the ways of combining 2D/3D shapes
• Dimensionally Extended 9-Intersection Model
• Meet (lattice theory)
• Intersection (set theory)
• Union (set theory)