Kaniadakis logistic distribution

The Kaniadakis Logistic distribution (also known as κ-Logisticdistribution) is a generalized version of the Logistic distribution associated with the Kaniadakis statistics. It is one example of a Kaniadakis distribution. The κ-Logistic probability distribution describes the population kinetics behavior of bosonic (${\displaystyle 0<\lambda <1}$) or fermionic (${\displaystyle \lambda >1}$) character.^[1]

κ-Logistic distribution

Probability density function Plot of the κ-Logistic distribution for typical κ-values and ${\displaystyle \beta =1}$. The case ${\displaystyle \kappa =0}$ corresponds to the ordinary Logistic distribution.
Cumulative distribution function Plots of the cumulative κ-Logistic distribution for typical κ-values and ${\displaystyle \beta =1}$. The case ${\displaystyle \kappa =0}$ corresponds to the ordinary Logistic case.
Parameters	${\displaystyle 0\leq \kappa <1}$ ${\displaystyle \alpha >0}$ shape (real) ${\displaystyle \beta >0}$ rate (real) ${\displaystyle \lambda >0}$
Support	${\displaystyle x\in [0,\infty )}$
PDF	${\displaystyle {\frac {\lambda \alpha \beta x^{\alpha -1}}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2\alpha }}}}{\frac {\exp _{\kappa }(-\beta x^{\alpha })}{[1+(\lambda -1)\exp _{\kappa }(-\beta x^{\alpha })]^{2}}}}$
CDF	${\displaystyle {\frac {1-\exp _{\kappa }(-\beta x^{\alpha })}{1+(\lambda -1)\exp _{\kappa }(-\beta x^{\alpha })}}}$

Definitions

Probability density function

The Kaniadakis κ-Logistic distribution is a four-parameter family of continuous statistical distributions, which is part of a class of statistical distributions emerging from the Kaniadakis κ-statistics. This distribution has the following probability density function:^[1]

${\displaystyle f_{_{\kappa }}(x)={\frac {\lambda \alpha \beta x^{\alpha -1}}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2\alpha }}}}{\frac {\exp _{\kappa }(-\beta x^{\alpha })}{[1+(\lambda -1)\exp _{\kappa }(-\beta x^{\alpha })]^{2}}}}$

valid for ${\displaystyle x\geq 0}$, where ${\displaystyle 0\leq |\kappa |<1}$ is the entropic index associated with the Kaniadakis entropy, ${\displaystyle \beta >0}$ is the rate parameter, ${\displaystyle \lambda >0}$, and ${\displaystyle \alpha >0}$ is the shape parameter.

The Logistic distribution is recovered as ${\displaystyle \kappa \rightarrow 0.}$

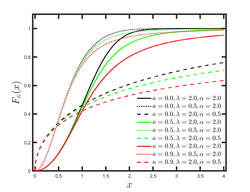
Cumulative distribution function

The cumulative distribution function of κ-Logistic is given by

${\displaystyle F_{\kappa }(x)={\frac {1-\exp _{\kappa }(-\beta x^{\alpha })}{1+(\lambda -1)\exp _{\kappa }(-\beta x^{\alpha })}}}$

valid for ${\displaystyle x\geq 0}$. The cumulative Logistic distribution is recovered in the classical limit ${\displaystyle \kappa \rightarrow 0}$.

Survival and hazard functions

The survival distribution function of κ-Logistic distribution is given by

${\displaystyle S_{\kappa }(x)={\frac {\lambda }{\exp _{\kappa }(\beta x^{\alpha })+\lambda -1}}}$

valid for ${\displaystyle x\geq 0}$. The survival Logistic distribution is recovered in the classical limit ${\displaystyle \kappa \rightarrow 0}$.

The hazard function associated with the κ-Logistic distribution is obtained by the solution of the following evolution equation:

${\displaystyle {\frac {S_{\kappa }(x)}{dx}}=-h_{\kappa }S_{\kappa }(x)\left(1-{\frac {\lambda -1}{\lambda }}S_{\kappa }(x)\right)}$

with ${\displaystyle S_{\kappa }(0)=1}$, where ${\displaystyle h_{\kappa }}$ is the hazard function:

${\displaystyle h_{\kappa }={\frac {\alpha \beta x^{\alpha -1}}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2\alpha }}}}}$

The cumulative Kaniadakis κ-Logistic distribution is related to the hazard function by the following expression:

${\displaystyle S_{\kappa }=e^{-H_{\kappa }(x)}}$

where ${\displaystyle H_{\kappa }(x)=\int _{0}^{x}h_{\kappa }(z)dz}$ is the cumulative hazard function. The cumulative hazard function of the Logistic distribution is recovered in the classical limit ${\displaystyle \kappa \rightarrow 0}$.

Related distributions

• The survival function of the κ-Logistic distribution represents the κ-deformation of the Fermi-Dirac function, and becomes a Fermi-Dirac distribution in the classical limit ${\displaystyle \kappa \rightarrow 0}$.^[1]
• The κ-Logistic distribution is a generalization of the κ-Weibull distribution when ${\displaystyle \lambda =1}$.
• A κ-Logistic distribution corresponds to a Half-Logistic distribution when ${\displaystyle \lambda =2}$, ${\displaystyle \alpha =1}$ and ${\displaystyle \kappa =0}$.
• The ordinary Logistic distribution is a particular case of a κ-Logistic distribution, when ${\displaystyle \kappa =0}$.

Applications

The κ-Logistic distribution has been applied in several areas, such as:

• In quantum statistics, the survival function of the κ-Logistic distribution represents the most general expression of the Fermi-Dirac function, reducing to the Fermi-Dirac distribution in the limit ${\displaystyle \kappa \rightarrow 0}$.^[2][3][4]

See also

• Giorgio Kaniadakis
• Kaniadakis statistics
• Kaniadakis distribution
• Kaniadakis κ-Exponential distribution
• Kaniadakis κ-Gaussian distribution
• Kaniadakis κ-Gamma distribution
• Kaniadakis κ-Weibull distribution
• Kaniadakis κ-Erlang distribution