Kaniadakis Weibull distribution

The Kaniadakis Weibull distribution (or κ-Weibull distribution) is a probability distribution arising as a generalization of the Weibull distribution.^[1][2] It is one example of a Kaniadakis κ-distribution. The κ-Weibull distribution has been adopted successfully for describing a wide variety of complex systems in seismology, economy, epidemiology, among many others.

κ-Weibull distribution

Probability density function
Cumulative distribution function
Parameters	${\displaystyle 0<\kappa <1}$ ${\displaystyle \alpha >0}$ rate shape (real) ${\displaystyle \beta >0}$ rate (real)
Support	${\displaystyle x\in [0,+\infty )}$
PDF	${\displaystyle {\frac {\alpha \beta x^{\alpha -1}}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2\alpha }}}}\exp _{\kappa }(-\beta x^{\alpha })}$
CDF	${\displaystyle 1-\exp _{\kappa }(-\beta x^{\alpha })}$
Quantile	${\displaystyle \beta ^{-1/\alpha }{\Bigg [}\ln _{\kappa }{\Bigg (}{\frac {1}{1-F_{\kappa }}}{\Bigg )}{\Bigg ]}^{1/\alpha }}$
Median	${\displaystyle \beta ^{-1/\alpha }{\Bigg (}\ln _{\kappa }(2){\Bigg )}^{1/\alpha }}$
Mode	${\displaystyle \beta ^{-1/\alpha }{\Bigg (}{\frac {\alpha ^{2}+2\kappa ^{2}(\alpha -1)}{2\kappa ^{2}(\alpha ^{2}-\kappa ^{2})}}{\sqrt {1+{\frac {4\kappa ^{2}(\alpha ^{2}-\kappa ^{2})(\alpha -1)^{2}}{[\alpha ^{2}+2\kappa ^{2}(\alpha -1)]^{2}}}}}-1{\Bigg )}^{1/2\alpha }}$
Method of moments	${\displaystyle {\frac {(2\kappa \beta )^{-m/\alpha }}{1+\kappa {\frac {m}{\alpha }}}}{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {m}{2\alpha }}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {m}{2\alpha }}{\Big )}}}\Gamma {\Big (}1+{\frac {m}{\alpha }}{\Big )}}$

Definitions

Probability density function

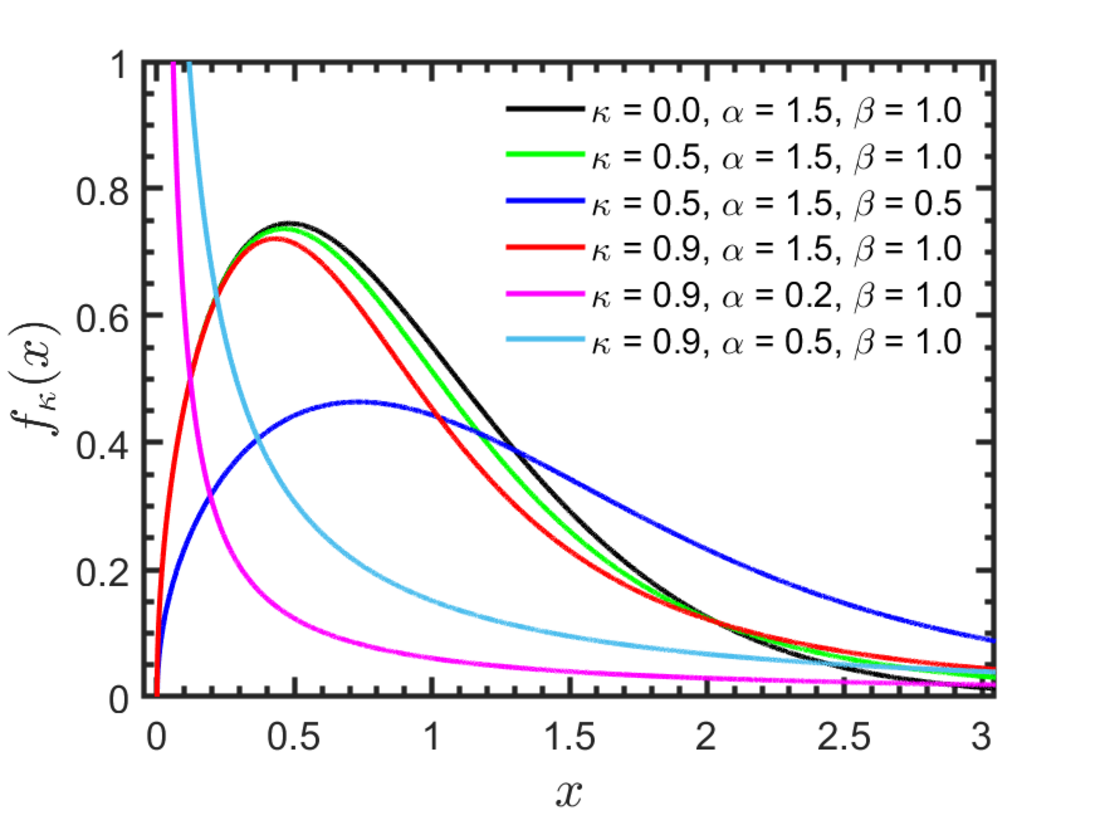
The Kaniadakis κ-Weibull distribution is exhibits power-law right tails, and it has the following probability density function:^[3]

${\displaystyle f_{_{\kappa }}(x)={\frac {\alpha \beta x^{\alpha -1}}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2\alpha }}}}\exp _{\kappa }(-\beta x^{\alpha })}$

valid for ${\displaystyle x\geq 0}$, where ${\displaystyle |\kappa |<1}$ is the entropic index associated with the Kaniadakis entropy, ${\displaystyle \beta >0}$ is the scale parameter, and ${\displaystyle \alpha >0}$ is the shape parameter or Weibull modulus.

The Weibull distribution is recovered as ${\displaystyle \kappa \rightarrow 0.}$

Cumulative distribution function

The cumulative distribution function of κ-Weibull distribution is given by

${\displaystyle F_{\kappa }(x)=1-\exp _{\kappa }(-\beta x^{\alpha })}$

valid for ${\displaystyle x\geq 0}$. The cumulative Weibull distribution is recovered in the classical limit ${\displaystyle \kappa \rightarrow 0}$.

Survival distribution and hazard functions

The survival distribution function of κ-Weibull distribution is given by

${\displaystyle S_{\kappa }(x)=\exp _{\kappa }(-\beta x^{\alpha })}$

valid for ${\displaystyle x\geq 0}$. The survival Weibull distribution is recovered in the classical limit ${\displaystyle \kappa \rightarrow 0}$.

Comparison between the Kaniadakis κ-Weibull probability function and its cumulative.

The hazard function of the κ-Weibull distribution is obtained through the solution of the κ-rate equation:

${\displaystyle {\frac {S_{\kappa }(x)}{dx}}=-h_{\kappa }S_{\kappa }(x)}$

with ${\displaystyle S_{\kappa }(0)=1}$, where ${\displaystyle h_{\kappa }}$ is the hazard function:

${\displaystyle h_{\kappa }={\frac {\alpha \beta x^{\alpha -1}}{\sqrt {1+\kappa ^{2}\beta ^{2}x^{2\alpha }}}}}$

The cumulative κ-Weibull distribution is related to the κ-hazard function by the following expression:

${\displaystyle S_{\kappa }=e^{-H_{\kappa }(x)}}$

where

${\displaystyle H_{\kappa }(x)=\int _{0}^{x}h_{\kappa }(z)dz}$

${\displaystyle H_{\kappa }(x)={\frac {1}{\kappa }}{\textrm {arcsinh}}\left(\kappa \beta x^{\alpha }\right)}$

is the cumulative κ-hazard function. The cumulative hazard function of the Weibull distribution is recovered in the classical limit ${\displaystyle \kappa \rightarrow 0}$: ${\displaystyle H(x)=\beta x^{\alpha }}$ .

Properties

Moments, median and mode

The κ-Weibull distribution has moment of order ${\displaystyle m\in \mathbb {N} }$ given by

${\displaystyle \operatorname {E} [X^{m}]={\frac {|2\kappa \beta |^{-m/\alpha }}{1+\kappa {\frac {m}{\alpha }}}}{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {m}{2\alpha }}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {m}{2\alpha }}{\Big )}}}\Gamma {\Big (}1+{\frac {m}{\alpha }}{\Big )}}$

The median and the mode are:

${\displaystyle x_{\textrm {median}}(F_{\kappa })=\beta ^{-1/\alpha }{\Bigg (}\ln _{\kappa }(2){\Bigg )}^{1/\alpha }}$

${\displaystyle x_{\textrm {mode}}=\beta ^{-1/\alpha }{\Bigg (}{\frac {\alpha ^{2}+2\kappa ^{2}(\alpha -1)}{2\kappa ^{2}(\alpha ^{2}-\kappa ^{2})}}{\Bigg )}^{1/2\alpha }{\Bigg (}{\sqrt {1+{\frac {4\kappa ^{2}(\alpha ^{2}-\kappa ^{2})(\alpha -1)^{2}}{[\alpha ^{2}+2\kappa ^{2}(\alpha -1)]^{2}}}}}-1{\Bigg )}^{1/2\alpha }\quad (\alpha >1)}$

Quantiles

The quantiles are given by the following expression

${\displaystyle x_{\textrm {quantile}}(F_{\kappa })=\beta ^{-1/\alpha }{\Bigg [}\ln _{\kappa }{\Bigg (}{\frac {1}{1-F_{\kappa }}}{\Bigg )}{\Bigg ]}^{1/\alpha }}$

with ${\displaystyle 0\leq F_{\kappa }\leq 1}$.

Gini coefficient

The Gini coefficient is:^[3]

${\displaystyle \operatorname {G} _{\kappa }=1-{\frac {\alpha +\kappa }{\alpha +{\frac {1}{2}}\kappa }}{\frac {\Gamma {\Big (}{\frac {1}{\kappa }}-{\frac {1}{2\alpha }}{\Big )}}{\Gamma {\Big (}{\frac {1}{\kappa }}+{\frac {1}{2\alpha }}{\Big )}}}{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {1}{2\alpha }}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {1}{2\alpha }}{\Big )}}}}$

Asymptotic behavior

The κ-Weibull distribution II behaves asymptotically as follows:^[3]

${\displaystyle \lim _{x\to +\infty }f_{\kappa }(x)\sim {\frac {\alpha }{\kappa }}(2\kappa \beta )^{-1/\kappa }x^{-1-\alpha /\kappa }}$

${\displaystyle \lim _{x\to 0^{+}}f_{\kappa }(x)=\alpha \beta x^{\alpha -1}}$

Related distributions

• The κ-Weibull distribution is a generalization of:
  • κ-Exponential distribution of type II, when ${\displaystyle \alpha =1}$;
  • Exponential distribution when ${\displaystyle \kappa =0}$ and ${\displaystyle \alpha =1}$.
• A κ-Weibull distribution corresponds to a κ-deformed Rayleigh distribution when ${\displaystyle \alpha =2}$ and a Rayleigh distribution when ${\displaystyle \kappa =0}$ and ${\displaystyle \alpha =2}$.

Applications

The κ-Weibull distribution has been applied in several areas, such as:

• In economy, for analyzing personal income models, in order to accurately describing simultaneously the income distribution among the richest part and the great majority of the population.^[1][4][5]
• In seismology, the κ-Weibull represents the statistical distribution of magnitude of the earthquakes distributed across the Earth, generalizing the Gutenberg–Richter law,^[6] and the interval distributions of seismic data, modeling extreme-event return intervals.^[7][8]
• In epidemiology, the κ-Weibull distribution presents a universal feature for epidemiological analysis.^[9]

See also

• Giorgio Kaniadakis
• Kaniadakis statistics
• Kaniadakis distribution
• Kaniadakis κ-Exponential distribution
• Kaniadakis κ-Gaussian distribution
• Kaniadakis κ-Gamma distribution
• Kaniadakis κ-Logistic distribution
• Kaniadakis κ-Erlang distribution