Kosnita's theorem

In Euclidean geometry, Kosnita's theorem is a property of certain circles associated with an arbitrary triangle.

X(54) is the Kosnita point of the triangle ABC

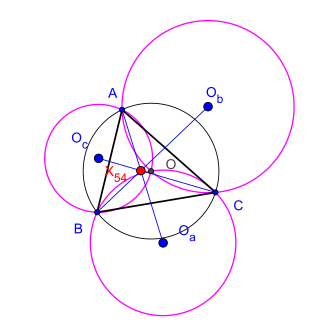
Let ${\displaystyle ABC}$ be an arbitrary triangle, ${\displaystyle O}$ its circumcenter and ${\displaystyle O_{a},O_{b},O_{c}}$ are the circumcenters of three triangles ${\displaystyle OBC}$, ${\displaystyle OCA}$, and ${\displaystyle OAB}$ respectively. The theorem claims that the three straight lines ${\displaystyle AO_{a}}$, ${\displaystyle BO_{b}}$, and ${\displaystyle CO_{c}}$ are concurrent.^[1] This result was established by the Romanian mathematician Cezar Coşniţă (1910-1962).^[2]

Their point of concurrence is known as the triangle's Kosnita point (named by Rigby in 1997). It is the isogonal conjugate of the nine-point center.^[3][4] It is triangle center ${\displaystyle X(54)}$ in Clark Kimberling's list.^[5] This theorem is a special case of Dao's theorem on six circumcenters associated with a cyclic hexagon in.^{[6][7][8][9][10][11][12]}