Line complex

In algebraic geometry, a line complex is a set of lines that can be specified by a list of homogeneous polynomial equations. That is, a projective variety of lines.

A linear line complex is defined by a list of degree-1 polynomials. A quadratic line complex is defined by a list of degree-2 polynomials. Similarly for cubic, quartic, quintic, sextic, etc.

They were first studied by Julius Plücker in Neue Geometrie des Raumes (1868). Other important figures include Felix Klein, Sophus Lie, Arthur Cayley, William Hamilton, and Alfred Clebsch.

Setup

By the standard trick in projective geometry, a line in 3-dimensional space is lifted to a plane through the origin in 4-dimensional space. In other words, the space of lines in ${\displaystyle \mathbb {R} ^{3}}$ is lifted to the space of planes through the origin in ${\displaystyle \mathbb {R} ^{4}}$, which is the Grassmannian ${\displaystyle G(2,4)}$. It is then embedded to the projective space ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{4})}$ via exterior product.

Note that during the projective embedding, we get lines that does not exist ${\displaystyle \mathbb {R} ^{3}}$: the lines at infinity.

${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{4})}$ is the projectivized space of bivectors in ${\displaystyle \mathbb {R} ^{4}}$, where ${\displaystyle \wedge }$ is the exterior product. The space has homogeneous coordinates (Plücker coordinates) ${\displaystyle [p_{12},p_{13},p_{14},p_{23},p_{24},p_{34}]}$. By convention, if ${\displaystyle p_{ij}}$ where ${\displaystyle i>j}$ is written, then ${\displaystyle p_{ij}:=-p_{ji}}$.

${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{4})}$ has 5 dimensions, and ${\displaystyle G(2,4)}$ has 4 dimensions.

A plane in ${\displaystyle G(2,4)}$ can be described by any two nonparallel vectors ${\displaystyle v,w}$, then it is mapped to ${\displaystyle [v\wedge w]}$ with coordinates ${\displaystyle p_{ij}=v_{i}w_{j}-v_{j}w_{i}}$. Thus we obtain an embedding ${\displaystyle p:G(2,4)\hookrightarrow \mathbb {P} (\wedge ^{2}\mathbb {R} ^{4})}$. It is not the whole ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{4})}$, but only a subvariety defined by the Klein quadric:$${\displaystyle p_{12}p_{34}+p_{13}p_{42}+p_{14}p_{23}=0}$$More succinctly, ${\displaystyle p\wedge p=0}$. Note that this is not a trivial condition, as a generic bivector does not satisfy it, for example ${\displaystyle (e_{1}\wedge e_{2}+e_{3}\wedge e_{4})}$.

From now on we will simply write ${\displaystyle G(2,4)}$ as if it is a subset of ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{4})}$, using the embedding.

Higher dimensions

The same construction shows that the space of lines in ${\displaystyle \mathbb {R} ^{n}}$ is lifted to ${\displaystyle G(2,n+1)}$, then embedded as a subvariety of ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{n+1})}$. Since ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{n+1})}$ has ${\displaystyle {\tfrac {1}{2}}n(n-1)-1}$ dimensions, and ${\displaystyle G(2,n+1)}$ has ${\displaystyle 2(n-2)}$ dimensions, it should be possible to write it as the intersection of ${\displaystyle {\tfrac {1}{2}}(n-2)(n-3)}$ hypersurfaces. However, ${\displaystyle G(2,\mathbb {R} ^{n})}$ is the intersection of the ${\displaystyle {\tfrac {1}{4}}n(n-1)(n-2)(n-3)}$ equations:$${\displaystyle Q_{ijkl}:=p_{ij}p_{kl}-p_{ik}p_{jl}+p_{il}p_{jk}=0\quad (1\leq i<j<k<l\leq n)}$$Thus, these equations must be dependent on each other when ${\displaystyle n\geq 5}$. This is called a sygyzy.

For example, when ${\displaystyle n=5}$, the space ${\displaystyle G(2,5)}$ is a codimension-3 subspace of ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{5})}$ defined as the intersection of 5 equations, so there are 2 redundancies, which can be exhibited by the matrix equation:$${\displaystyle {\begin{pmatrix}0&p_{12}&p_{13}&p_{14}&p_{15}\\-p_{12}&0&p_{23}&p_{24}&p_{25}\\-p_{13}&-p_{23}&0&p_{34}&p_{35}\\-p_{14}&-p_{24}&-p_{34}&0&p_{45}\\-p_{15}&-p_{25}&-p_{35}&-p_{45}&0\end{pmatrix}}{\begin{pmatrix}Q_{1}\\Q_{2}\\Q_{3}\\Q_{4}\\Q_{5}\end{pmatrix}}=0,\quad {\begin{aligned}Q_{1}&=p_{23}p_{45}-p_{24}p_{35}+p_{25}p_{34}\\Q_{2}&=p_{13}p_{45}-p_{14}p_{35}+p_{15}p_{34}\\Q_{3}&=p_{12}p_{45}-p_{14}p_{25}+p_{15}p_{24}\\Q_{4}&=p_{12}p_{35}-p_{13}p_{25}+p_{15}p_{23}\\Q_{5}&=p_{12}p_{34}-p_{13}p_{24}+p_{14}p_{23}.\end{aligned}}}$$In the subspace of ${\displaystyle \mathbb {A} ^{9}\subset \mathbb {P} (\wedge ^{2}\mathbb {R} ^{5})}$ where ${\displaystyle p_{12}=1}$, the two linear syzygies$${\displaystyle Q_{1}=p_{23}Q_{3}+p_{24}Q_{4}+p_{25}Q_{5},\quad Q_{2}=-p_{13}Q_{3}-p_{14}Q_{4}-p_{15}Q_{5}}$$show that if ${\displaystyle Q_{3},Q_{4},Q_{5}=0}$, then the other two conditions are automatically satisfied. This is the redundancy.

Special families of lines

A ruled surface in ${\displaystyle \mathbb {R} ^{3}}$ is a curve in the Klein quadric ${\displaystyle G(2,4)\subset \mathbb {P} (\wedge ^{2}\mathbb {R} ^{4})}$. A ruled surface is a line complex when it is the intersection of 3 line complexes, each defined by a single homogeneous polynomial on ${\displaystyle \wedge ^{2}\mathbb {R} ^{4}}$.

In general, a ruled surface is a 1-parameter family of lines. A congruence of lines is a 2-parameter family. A particular example is the set of lines in ${\displaystyle \mathbb {R} ^{3}}$ orthogonal to a given surface. The Malus–Dupin theorem shows that geometric optics preserves orthogonal congruences.

Linear line complex

A linear line complex is the intersection of ${\displaystyle G(2,4)}$ with one or more hyperplanes in ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{4})}$, which would be defined by a homogeneous linear equation. Equivalently, it is defined as the space of planes through the origin in ${\displaystyle \mathbb {R} ^{4}}$ which make a 2-form in ${\displaystyle \wedge ^{2}\mathbb {R} ^{4}}$ equal to zero.

The standard contact structure is isomorphic to the cylindrically symmetric ${\displaystyle dz-r^{2}d\theta }$.

For example, ${\displaystyle p_{12}+p_{34}=0}$ defines the space of planes through the origin in ${\displaystyle \mathbb {R} ^{4}}$ which make ${\displaystyle \omega$ :=dx_{1}\wedge dx_{2}+dx_{3}\wedge dx_{4}} equal to 0. There are ${\displaystyle \infty ^{3}}$ such planes. Equivalently, it is a 3-dimensional space of lines in ${\displaystyle \mathbb {R} ^{3}}$ (plus the lines at infinity), which satisfy ${\displaystyle v_{2}w_{1}-v_{1}w_{2}+w_{3}=0}$ given any ${\displaystyle \{v+tw:t\in \mathbb {R} \}}$ parameterization of the line. Equivalently, these are lines that are tangent to the cylindrical contact structure on ${\displaystyle \mathbb {R} ^{3}}$:$${\displaystyle dz-xdy+ydx=dz-r^{2}d\theta }$$That is, they are linear Legendrian submanifolds.

More generally, ${\displaystyle p_{12}+\dots +p_{2n-1,2n}=0}$ defines the space of planes through the origin in ${\displaystyle \mathbb {R} ^{2n}}$ which make ${\displaystyle \omega$ :=dx_{1}\wedge dx_{2}+\dots +dx_{2n-1}\wedge dx_{2n}} equal to 0. There are ${\displaystyle \infty ^{2n-5}}$ such planes. This form ${\displaystyle \omega }$ is a symplectic form, These planes are known as the isotropic planes of ${\displaystyle \omega }$.

Symplectic transformation

Any linear transformation of ${\displaystyle \mathbb {R} ^{n}}$ induces a transformation of ${\displaystyle \wedge ^{2}\mathbb {R} ^{n+1}}$ that preserves ${\displaystyle G(2,n+1)}$. If the transformation also preserves ${\displaystyle \omega }$, then it is a symplectic transformation. In the spirit of Erlangen program, symplectic geometry studies invariants of symplectic transformations.

Symplectic transformations make up a group, called the symplectic group. The group acts on ${\displaystyle \mathbb {R} ^{n}}$, splitting it into 2 orbits: one orbit for nonzero vectors, and another orbit for 0. It acts on ${\displaystyle G(2,n+1)}$ as well, splitting it into 2 orbits: one orbit for isotropic planes, and another orbit for symplectic planes. More generally, any projective transformation on ${\displaystyle \mathbb {P} (\mathbb {R} ^{n})}$ that preserves the linear line complex defined by ${\displaystyle \omega }$ is a symplectic transformation. This is why Lie always referred to the symplectic group as "the projective group of a linear line complex".^[1]

Degeneracy

A 2-form ${\displaystyle \sigma }$ on ${\displaystyle \mathbb {R} ^{n+1}}$ can be nondegenerate or degenerate. The symplectic form is nondegenerate.

In the degenerate case, its kernel is a nontrivial even-dimensional linear subspace: ${\displaystyle \ker \sigma$ :=\{v\in \mathbb {R} ^{n+1}|\sigma (v,\cdot )=0\}\subset \mathbb {R} ^{n+1}} , which projectives to an odd-dimensional flat in ${\displaystyle \mathbb {P} (\mathbb {R} ^{n+1})}$.

A degenerate but nonzero 2-form on ${\displaystyle \mathbb {R} ^{4}}$ has a 2-dimensional kernel, which projectivizes to a line in ${\displaystyle \mathbb {R} ^{3}}$. Plücker called a linear line complex defined by a degenerate ${\displaystyle \sigma }$ special, and ${\displaystyle \ker \sigma }$ its axis.

Involution

Define the bilinear form ${\displaystyle B(p,q):=\sum _{i<j}p_{ij}q_{ij}}$ on ${\displaystyle \wedge ^{2}\mathbb {R} ^{n}}$. Two linear line complexes defined by two linear subspaces ${\displaystyle V,W\subset \wedge ^{2}\mathbb {R} ^{n}}$ are in involution, or in Klein polarity, if ${\displaystyle V,W}$ are orthogonal complements relative to ${\displaystyle B}$.

Pencils

Through a point in ${\displaystyle \mathbb {R} ^{n}}$, a planar pencil is the set of all lines through this point within a 2-dimensional plane. It is embedded to a straight line in ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{n+1})}$.

More generally, the set of all lines through this point within a k-flat is embedded to a (k-1)-flat in ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{n+1})}$.

Given a 2-flat ${\displaystyle F\subset \mathbb {R} ^{n}}$, the set of all lines in it is enumerated by the pencils of each point in a line. It is embedded to a 2-flat in ${\displaystyle p(F)\subset \mathbb {P} (\wedge ^{2}\mathbb {R} ^{n+1})}$. This can be regarded as a planar pencil of a point at infinity. Dually, for each ${\displaystyle p(l)\in p(F)}$, there is a planar pencil of lines in ${\displaystyle p(F)}$. Each line in the pencil of ${\displaystyle p(l)}$ corresponds to a pencil in a point in ${\displaystyle l\subset F}$.

More generally, the set of all lines within a k-flat is embedded to a (2k-2)-flat in ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{n+1})}$.

Constraints

A string model of a portion of a regulus and its opposite to show the rules on a hyperboloid of one sheet

In general, the set of all lines that satisfy a number of linear constraints is a linear line complex.

In ${\displaystyle \mathbb {R} ^{3}}$, the linear constraints include: passing a point, intersecting a line, and parallel to a plane. The set of all lines that intersect 2 lines and parallel to a plane (in general position) is a doubly ruled surface defined by intersecting 3 linear line complexes. In general, the set of all lines that satisfy 3 linear constraints is a regulus defined by intersecting 3 linear line complexes.

More exotic examples are available. For example, the aforementioned family of Legendrian lines defined by ${\displaystyle p_{12}+p_{34}=0}$ is a linear line complex, which can be interpreted as a linear constraint of ${\displaystyle dz-xdy+ydx}$.

Quadratic line complex

A quadratic line complex is obtained by intersecting ${\displaystyle G(2,n+1)}$ with quadratic hypersurfaces in ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{n+1})}$. In homogeneous coordinates, they are of form ${\displaystyle p^{T}Mp}$, where ${\displaystyle M}$ is a ${\displaystyle {\tfrac {1}{2}}n(n+1)\times {\tfrac {1}{2}}n(n+1)}$ symmetric matrix.

In the case of ${\displaystyle n=3}$, a general quadratic line complex is specified by a quadratic form on ${\displaystyle \mathbb {P} (\wedge ^{2}\mathbb {R} ^{3})}$ modulo the Klein quadric, resulting in 19 parameters. In general, ${\displaystyle {\binom {{\tfrac {1}{2}}n(n+1)}{2}}-{\binom {n+1}{4}}-1}$ parameters are necessary.

The tangent developable of a helix

In general, the set of all lines that satisfy a number of linear constraints, and at least one quadratic constraint is a quadratic line complex. Examples in ${\displaystyle \mathbb {R} ^{3}}$:

• Intersect a conic section.
• Tangent to a quadratic surface. In particular, fixed distance from a point (i.e. tangent to a sphere) and fixed distance from a line (i.e. tangent to a cylinder).
• Parallel to exactly line in a nondegenerate quadratic cone (i.e. a cone whose cross-section is a conic section). In particular, all lines that make a fixed angle to a plane (i.e. parallel to a line in a circular cone). Equivalently, all lines that make a fixed skew-angle to a line.

• Given two quadratic surfaces and a real number ${\displaystyle c}$, the lines that intersect the two surfaces at 4 points whose cross-ratio is equal to ${\displaystyle c}$ forms a quadratic line complex. These are the harmonic complexes.

The intersection of 3 linear/quadratic constraints in general position produces a ruled surface. For example, the tangent developable of a helix is obtained by intersecting the 3 constraints of: tangent to a cylinder, makes a fixed angle with a plane, and in the Legendrian line complex. Thus it is a quadratic line complex.

Tetrahedral

In the special case where the two quadratic surfaces degenerate into 4 planes, the lines that intersect the 4 planes at 4 points whose cross-ratio is equal to a fixed number forms a quadratic line complex. This is a tetrahedral complex, which is a special case of the harmonic complex.

von Staudt's theorem: given a line ${\displaystyle l}$ in general position with a tetrahedron with vertices ${\displaystyle ABCD}$ and their respective faces ${\displaystyle abcd}$, the cross-ratio of the 4 planes ${\displaystyle [lA,lB,lC,lD]}$ is equal to the cross-ratio of the 4 points ${\displaystyle [l\cap a,l\cap b,l\cap c,l\cap d]}$.

For any quadratic complex and linear complex in general position, their intersection is contained in a tetrahedral complex.

Singular

Kummer's surface.

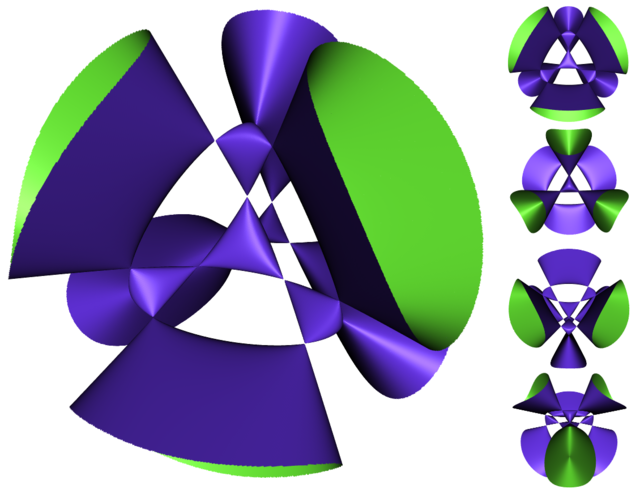
In general, a quadratic line complex defined by a single quadratic equation has 3 dimensions, so through each point in ${\displaystyle \mathbb {R} ^{3}}$ there exists a whole 1-dimensional pencil of lines that sweeps out a quadratic cone. This can be constructed by intersecting the quadratic constraint with the linear constraint of "passing to a point".

However, there exists a 2-dimensional set of points where this breaks down. Specifically, at these points, the quadratic cone degenerates into two flat planes. These points are the singular points of the quadratic line complex. The set of these points is its singular surface. The singular surface is Kummer's surface. It is a quartic surface. Each line meets the surface in 4 points, and through each line there are 4 tangent planes to the surface. It has 16 singular points ("nodes") and 16 singular planes ("tropes"), the maximum possible for a quartic surface. There are 6 nodes lying in each of the 16 tropes and 6 tropes passing through each of the 16 nodes.

Similarly, each plane in ${\displaystyle \mathbb {R} ^{3}}$ intersects a quadratic line complex at a 1-dimensional quadratic line complex. In general, these lines sweep out a conic section as their envelope. However, there exists a 2-dimensional set of planes where this breaks down. These planes are the singular planes. The envelope of these planes is once again the same singular surface.

There is a 1-dimensional family of infinite number of quadratic complexes having the same singular surface. These are called cosingular complexes.

Higher line complex

Whitney umbrella as a ruled surface, generated by a moving straight line

A ruled surface is a 1-parameter family of lines ${\displaystyle \mathbb {R} ^{3}}$. They can be obtained by intersecting 3 constraints in general position. The only structurally stable singularity that can appear in a ruled surface is the cross-cap, which looks like a Whitney unbrella.^[2]

A congruence of lines is a 2-parameter family in ${\displaystyle \mathbb {R} ^{3}}$, and are obtained by intersecting 2 constraints in general position. In general, through each point in ${\displaystyle \mathbb {R} ^{3}}$ there passes exactly ${\displaystyle n}$ lines of the congruence, and through each plane in ${\displaystyle \mathbb {R} ^{3}}$ there passes exactly ${\displaystyle m}$ lines of the congruence. Such a congruence is said to be of order ${\displaystyle n}$ and class ${\displaystyle m}$.

In particular, the intersection of a quadratic complex with a linear complex is a congruence with order 2 and class 2.

History

At the death of Julius Plücker, his Neue Geometrie des Raumes was completed by his pupil Felix Klein in 1868. Klein used invariant theory that he learned from Alfred Clebsch.

Klein and Lie studied line complexes, especially tetrahedral complexes. The group of all projective transformations that stabilizes the 4 vertices of the tetrahedron is a 3-dimensional abelian Lie group ${\displaystyle G}$. For any two points ${\displaystyle x,y}$ in general position with the tetrahedron, there exists a unique ${\displaystyle g\in G}$ such that ${\displaystyle g(x)=y}$. Each tetrahedral complex is obtained as the orbit of a single line under the action of ${\displaystyle G}$.

Lie asked Klein whether there are curves ${\displaystyle \gamma }$ such that, if ${\displaystyle g\in G}$ maps some ${\displaystyle x\in \gamma }$ to some ${\displaystyle g(x)\in \gamma }$, then ${\displaystyle g}$ also maps the tangent line ${\displaystyle T_{x}\gamma }$ to the tangent line ${\displaystyle T_{g(x)}\gamma }$. Klein discovered that there are curves which are stabilized by a 1-dimensional subgroup of ${\displaystyle G}$. He called these the W-curves. Since the curve is essentially translated by the action of the group, it necessarily maps tangents to tangents. This was an application of Lie algebra in the prehistory of Lie group theory. The investigation of such linear complexes also inspired Klein to propose the Erlangen program.^[1][3]

Their line of work in line geometry was taken up by Corrado Segre, whose work, including the classification of quadratic line complexes, was foundation in the Italian school of algebraic geometry.^[4]