B8 polytope

In 8-dimensional geometry, there are 256 uniform polytopes with B₈ symmetry. There are two regular forms, the 8-orthoplex and 8-cube, with 16 and 256 vertices respectively. The 8-demicube is added with half the symmetry.

Orthographic projections in the B₈ Coxeter plane

8-cube

8-orthoplex

8-demicube

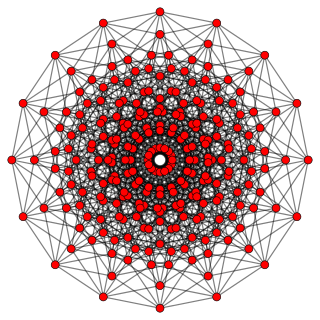
They can be visualized as symmetric orthographic projections in Coxeter planes of the B₈ Coxeter group, and other subgroups.

Graphs

Symmetric orthographic projections of these 256 polytopes can be made in the B₈, B₇, B₆, B₅, B₄, B₃, B₂, A₇, A₅, A₃, Coxeter planes. A_k has [k+1] symmetry, and B_k has [2k] symmetry.

These 256 polytopes are each shown in these 10 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.

#	Element counts										Coxeter-Dynkin diagram Schläfli symbol Name
	B8 [16]	B7 [14]	B6 [12]	B5 [10]	B4 [8]	B3 [6]	B2 [4]	A7 [8]	A5 [6]	A3 [4]
1											t0{3,3,3,3,3,3,4} 8-orthoplex Diacosipentacontahexazetton (ek)
2											t1{3,3,3,3,3,3,4} Rectified 8-orthoplex Rectified diacosipentacontahexazetton (rek)
3											t2{3,3,3,3,3,3,4} Birectified 8-orthoplex Birectified diacosipentacontahexazetton (bark)
4											t3{3,3,3,3,3,3,4} Trirectified 8-orthoplex Trirectified diacosipentacontahexazetton (tark)
5											t3{4,3,3,3,3,3,3} Trirectified 8-cube Trirectified octeract (tro)
6											t2{4,3,3,3,3,3,3} Birectified 8-cube Birectified octeract (bro)
7											t1{4,3,3,3,3,3,3} Rectified 8-cube Rectified octeract (recto)
8											t0{4,3,3,3,3,3,3} 8-cube Octeract (octo)
9											t0,1{3,3,3,3,3,3,4} Truncated 8-orthoplex Truncated diacosipentacontahexazetton (tek)
10											t0,2{3,3,3,3,3,3,4} Cantellated 8-orthoplex Small rhombated diacosipentacontahexazetton (srek)
11											t1,2{3,3,3,3,3,3,4} Bitruncated 8-orthoplex Bitruncated diacosipentacontahexazetton (batek)
12											t0,3{3,3,3,3,3,3,4} Runcinated 8-orthoplex Small prismated diacosipentacontahexazetton (spek)
13											t1,3{3,3,3,3,3,3,4} Bicantellated 8-orthoplex Small birhombated diacosipentacontahexazetton (sabork)
14											t2,3{3,3,3,3,3,3,4} Tritruncated 8-orthoplex Tritruncated diacosipentacontahexazetton (tatek)
15											t0,4{3,3,3,3,3,3,4} Stericated 8-orthoplex Small cellated diacosipentacontahexazetton (scak)
16											t1,4{3,3,3,3,3,3,4} Biruncinated 8-orthoplex Small biprismated diacosipentacontahexazetton (sabpek)
17											t2,4{3,3,3,3,3,3,4} Tricantellated 8-orthoplex Small trirhombated diacosipentacontahexazetton (satrek)
18											t3,4{4,3,3,3,3,3,3} Quadritruncated 8-cube Octeractidiacosipentacontahexazetton (oke)
19											t0,5{3,3,3,3,3,3,4} Pentellated 8-orthoplex Small terated diacosipentacontahexazetton (setek)
20											t1,5{3,3,3,3,3,3,4} Bistericated 8-orthoplex Small bicellated diacosipentacontahexazetton (sibcak)
21											t2,5{4,3,3,3,3,3,3} Triruncinated 8-cube Small triprismato-octeractidiacosipentacontahexazetton (sitpoke)
22											t2,4{4,3,3,3,3,3,3} Tricantellated 8-cube Small trirhombated octeract (satro)
23											t2,3{4,3,3,3,3,3,3} Tritruncated 8-cube Tritruncated octeract (tato)
24											t0,6{3,3,3,3,3,3,4} Hexicated 8-orthoplex Small petated diacosipentacontahexazetton (supek)
25											t1,6{4,3,3,3,3,3,3} Bipentellated 8-cube Small biteri-octeractidiacosipentacontahexazetton (sabtoke)
26											t1,5{4,3,3,3,3,3,3} Bistericated 8-cube Small bicellated octeract (sobco)
27											t1,4{4,3,3,3,3,3,3} Biruncinated 8-cube Small biprismated octeract (sabepo)
28											t1,3{4,3,3,3,3,3,3} Bicantellated 8-cube Small birhombated octeract (subro)
29											t1,2{4,3,3,3,3,3,3} Bitruncated 8-cube Bitruncated octeract (bato)
30											t0,7{4,3,3,3,3,3,3} Heptellated 8-cube Small exi-octeractidiacosipentacontahexazetton (saxoke)
31											t0,6{4,3,3,3,3,3,3} Hexicated 8-cube Small petated octeract (supo)
32											t0,5{4,3,3,3,3,3,3} Pentellated 8-cube Small terated octeract (soto)
33											t0,4{4,3,3,3,3,3,3} Stericated 8-cube Small cellated octeract (soco)
34											t0,3{4,3,3,3,3,3,3} Runcinated 8-cube Small prismated octeract (sopo)
35											t0,2{4,3,3,3,3,3,3} Cantellated 8-cube Small rhombated octeract (soro)
36											t0,1{4,3,3,3,3,3,3} Truncated 8-cube Truncated octeract (tocto)
37											t0,1,2{3,3,3,3,3,3,4} Cantitruncated 8-orthoplex Great rhombated diacosipentacontahexazetton
38											t0,1,3{3,3,3,3,3,3,4} Runcitruncated 8-orthoplex Prismatotruncated diacosipentacontahexazetton
39											t0,2,3{3,3,3,3,3,3,4} Runcicantellated 8-orthoplex Prismatorhombated diacosipentacontahexazetton
40											t1,2,3{3,3,3,3,3,3,4} Bicantitruncated 8-orthoplex Great birhombated diacosipentacontahexazetton
41											t0,1,4{3,3,3,3,3,3,4} Steritruncated 8-orthoplex Cellitruncated diacosipentacontahexazetton
42											t0,2,4{3,3,3,3,3,3,4} Stericantellated 8-orthoplex Cellirhombated diacosipentacontahexazetton
43											t1,2,4{3,3,3,3,3,3,4} Biruncitruncated 8-orthoplex Biprismatotruncated diacosipentacontahexazetton
44											t0,3,4{3,3,3,3,3,3,4} Steriruncinated 8-orthoplex Celliprismated diacosipentacontahexazetton
45											t1,3,4{3,3,3,3,3,3,4} Biruncicantellated 8-orthoplex Biprismatorhombated diacosipentacontahexazetton
46											t2,3,4{3,3,3,3,3,3,4} Tricantitruncated 8-orthoplex Great trirhombated diacosipentacontahexazetton
47											t0,1,5{3,3,3,3,3,3,4} Pentitruncated 8-orthoplex Teritruncated diacosipentacontahexazetton
48											t0,2,5{3,3,3,3,3,3,4} Penticantellated 8-orthoplex Terirhombated diacosipentacontahexazetton
49											t1,2,5{3,3,3,3,3,3,4} Bisteritruncated 8-orthoplex Bicellitruncated diacosipentacontahexazetton
50											t0,3,5{3,3,3,3,3,3,4} Pentiruncinated 8-orthoplex Teriprismated diacosipentacontahexazetton
51											t1,3,5{3,3,3,3,3,3,4} Bistericantellated 8-orthoplex Bicellirhombated diacosipentacontahexazetton
52											t2,3,5{3,3,3,3,3,3,4} Triruncitruncated 8-orthoplex Triprismatotruncated diacosipentacontahexazetton
53											t0,4,5{3,3,3,3,3,3,4} Pentistericated 8-orthoplex Tericellated diacosipentacontahexazetton
54											t1,4,5{3,3,3,3,3,3,4} Bisteriruncinated 8-orthoplex Bicelliprismated diacosipentacontahexazetton
55											t2,3,5{4,3,3,3,3,3,3} Triruncitruncated 8-cube Triprismatotruncated octeract
56											t2,3,4{4,3,3,3,3,3,3} Tricantitruncated 8-cube Great trirhombated octeract
57											t0,1,6{3,3,3,3,3,3,4} Hexitruncated 8-orthoplex Petitruncated diacosipentacontahexazetton
58											t0,2,6{3,3,3,3,3,3,4} Hexicantellated 8-orthoplex Petirhombated diacosipentacontahexazetton
59											t1,2,6{3,3,3,3,3,3,4} Bipentitruncated 8-orthoplex Biteritruncated diacosipentacontahexazetton
60											t0,3,6{3,3,3,3,3,3,4} Hexiruncinated 8-orthoplex Petiprismated diacosipentacontahexazetton
61											t1,3,6{3,3,3,3,3,3,4} Bipenticantellated 8-orthoplex Biterirhombated diacosipentacontahexazetton
62											t1,4,5{4,3,3,3,3,3,3} Bisteriruncinated 8-cube Bicelliprismated octeract
63											t0,4,6{3,3,3,3,3,3,4} Hexistericated 8-orthoplex Peticellated diacosipentacontahexazetton
64											t1,3,6{4,3,3,3,3,3,3} Bipenticantellated 8-cube Biterirhombated octeract
65											t1,3,5{4,3,3,3,3,3,3} Bistericantellated 8-cube Bicellirhombated octeract
66											t1,3,4{4,3,3,3,3,3,3} Biruncicantellated 8-cube Biprismatorhombated octeract
67											t0,5,6{3,3,3,3,3,3,4} Hexipentellated 8-orthoplex Petiterated diacosipentacontahexazetton
68											t1,2,6{4,3,3,3,3,3,3} Bipentitruncated 8-cube Biteritruncated octeract
69											t1,2,5{4,3,3,3,3,3,3} Bisteritruncated 8-cube Bicellitruncated octeract
70											t1,2,4{4,3,3,3,3,3,3} Biruncitruncated 8-cube Biprismatotruncated octeract
71											t1,2,3{4,3,3,3,3,3,3} Bicantitruncated 8-cube Great birhombated octeract
72											t0,1,7{3,3,3,3,3,3,4} Heptitruncated 8-orthoplex Exitruncated diacosipentacontahexazetton
73											t0,2,7{3,3,3,3,3,3,4} Hepticantellated 8-orthoplex Exirhombated diacosipentacontahexazetton
74											t0,5,6{4,3,3,3,3,3,3} Hexipentellated 8-cube Petiterated octeract
75											t0,3,7{3,3,3,3,3,3,4} Heptiruncinated 8-orthoplex Exiprismated diacosipentacontahexazetton
76											t0,4,6{4,3,3,3,3,3,3} Hexistericated 8-cube Peticellated octeract
77											t0,4,5{4,3,3,3,3,3,3} Pentistericated 8-cube Tericellated octeract
78											t0,3,7{4,3,3,3,3,3,3} Heptiruncinated 8-cube Exiprismated octeract
79											t0,3,6{4,3,3,3,3,3,3} Hexiruncinated 8-cube Petiprismated octeract
80											t0,3,5{4,3,3,3,3,3,3} Pentiruncinated 8-cube Teriprismated octeract
81											t0,3,4{4,3,3,3,3,3,3} Steriruncinated 8-cube Celliprismated octeract
82											t0,2,7{4,3,3,3,3,3,3} Hepticantellated 8-cube Exirhombated octeract
83											t0,2,6{4,3,3,3,3,3,3} Hexicantellated 8-cube Petirhombated octeract
84											t0,2,5{4,3,3,3,3,3,3} Penticantellated 8-cube Terirhombated octeract
85											t0,2,4{4,3,3,3,3,3,3} Stericantellated 8-cube Cellirhombated octeract
86											t0,2,3{4,3,3,3,3,3,3} Runcicantellated 8-cube Prismatorhombated octeract
87											t0,1,7{4,3,3,3,3,3,3} Heptitruncated 8-cube Exitruncated octeract
88											t0,1,6{4,3,3,3,3,3,3} Hexitruncated 8-cube Petitruncated octeract
89											t0,1,5{4,3,3,3,3,3,3} Pentitruncated 8-cube Teritruncated octeract
90											t0,1,4{4,3,3,3,3,3,3} Steritruncated 8-cube Cellitruncated octeract
91											t0,1,3{4,3,3,3,3,3,3} Runcitruncated 8-cube Prismatotruncated octeract
92											t0,1,2{4,3,3,3,3,3,3} Cantitruncated 8-cube Great rhombated octeract
93											t0,1,2,3{3,3,3,3,3,3,4} Runcicantitruncated 8-orthoplex Great prismated diacosipentacontahexazetton
94											t0,1,2,4{3,3,3,3,3,3,4} Stericantitruncated 8-orthoplex Celligreatorhombated diacosipentacontahexazetton
95											t0,1,3,4{3,3,3,3,3,3,4} Steriruncitruncated 8-orthoplex Celliprismatotruncated diacosipentacontahexazetton
96											t0,2,3,4{3,3,3,3,3,3,4} Steriruncicantellated 8-orthoplex Celliprismatorhombated diacosipentacontahexazetton
97											t1,2,3,4{3,3,3,3,3,3,4} Biruncicantitruncated 8-orthoplex Great biprismated diacosipentacontahexazetton
98											t0,1,2,5{3,3,3,3,3,3,4} Penticantitruncated 8-orthoplex Terigreatorhombated diacosipentacontahexazetton
99											t0,1,3,5{3,3,3,3,3,3,4} Pentiruncitruncated 8-orthoplex Teriprismatotruncated diacosipentacontahexazetton
100											t0,2,3,5{3,3,3,3,3,3,4} Pentiruncicantellated 8-orthoplex Teriprismatorhombated diacosipentacontahexazetton
101											t1,2,3,5{3,3,3,3,3,3,4} Bistericantitruncated 8-orthoplex Bicelligreatorhombated diacosipentacontahexazetton
102											t0,1,4,5{3,3,3,3,3,3,4} Pentisteritruncated 8-orthoplex Tericellitruncated diacosipentacontahexazetton
103											t0,2,4,5{3,3,3,3,3,3,4} Pentistericantellated 8-orthoplex Tericellirhombated diacosipentacontahexazetton
104											t1,2,4,5{3,3,3,3,3,3,4} Bisteriruncitruncated 8-orthoplex Bicelliprismatotruncated diacosipentacontahexazetton
105											t0,3,4,5{3,3,3,3,3,3,4} Pentisteriruncinated 8-orthoplex Tericelliprismated diacosipentacontahexazetton
106											t1,3,4,5{3,3,3,3,3,3,4} Bisteriruncicantellated 8-orthoplex Bicelliprismatorhombated diacosipentacontahexazetton
107											t2,3,4,5{4,3,3,3,3,3,3} Triruncicantitruncated 8-cube Great triprismato-octeractidiacosipentacontahexazetton
108											t0,1,2,6{3,3,3,3,3,3,4} Hexicantitruncated 8-orthoplex Petigreatorhombated diacosipentacontahexazetton
109											t0,1,3,6{3,3,3,3,3,3,4} Hexiruncitruncated 8-orthoplex Petiprismatotruncated diacosipentacontahexazetton
110											t0,2,3,6{3,3,3,3,3,3,4} Hexiruncicantellated 8-orthoplex Petiprismatorhombated diacosipentacontahexazetton
111											t1,2,3,6{3,3,3,3,3,3,4} Bipenticantitruncated 8-orthoplex Biterigreatorhombated diacosipentacontahexazetton
112											t0,1,4,6{3,3,3,3,3,3,4} Hexisteritruncated 8-orthoplex Peticellitruncated diacosipentacontahexazetton
113											t0,2,4,6{3,3,3,3,3,3,4} Hexistericantellated 8-orthoplex Peticellirhombated diacosipentacontahexazetton
114											t1,2,4,6{3,3,3,3,3,3,4} Bipentiruncitruncated 8-orthoplex Biteriprismatotruncated diacosipentacontahexazetton
115											t0,3,4,6{3,3,3,3,3,3,4} Hexisteriruncinated 8-orthoplex Peticelliprismated diacosipentacontahexazetton
116											t1,3,4,6{4,3,3,3,3,3,3} Bipentiruncicantellated 8-cube Biteriprismatorhombi-octeractidiacosipentacontahexazetton
117											t1,3,4,5{4,3,3,3,3,3,3} Bisteriruncicantellated 8-cube Bicelliprismatorhombated octeract
118											t0,1,5,6{3,3,3,3,3,3,4} Hexipentitruncated 8-orthoplex Petiteritruncated diacosipentacontahexazetton
119											t0,2,5,6{3,3,3,3,3,3,4} Hexipenticantellated 8-orthoplex Petiterirhombated diacosipentacontahexazetton
120											t1,2,5,6{4,3,3,3,3,3,3} Bipentisteritruncated 8-cube Bitericellitrunki-octeractidiacosipentacontahexazetton
121											t0,3,5,6{3,3,3,3,3,3,4} Hexipentiruncinated 8-orthoplex Petiteriprismated diacosipentacontahexazetton
122											t1,2,4,6{4,3,3,3,3,3,3} Bipentiruncitruncated 8-cube Biteriprismatotruncated octeract
123											t1,2,4,5{4,3,3,3,3,3,3} Bisteriruncitruncated 8-cube Bicelliprismatotruncated octeract
124											t0,4,5,6{3,3,3,3,3,3,4} Hexipentistericated 8-orthoplex Petitericellated diacosipentacontahexazetton
125											t1,2,3,6{4,3,3,3,3,3,3} Bipenticantitruncated 8-cube Biterigreatorhombated octeract
126											t1,2,3,5{4,3,3,3,3,3,3} Bistericantitruncated 8-cube Bicelligreatorhombated octeract
127											t1,2,3,4{4,3,3,3,3,3,3} Biruncicantitruncated 8-cube Great biprismated octeract
128											t0,1,2,7{3,3,3,3,3,3,4} Hepticantitruncated 8-orthoplex Exigreatorhombated diacosipentacontahexazetton
129											t0,1,3,7{3,3,3,3,3,3,4} Heptiruncitruncated 8-orthoplex Exiprismatotruncated diacosipentacontahexazetton
130											t0,2,3,7{3,3,3,3,3,3,4} Heptiruncicantellated 8-orthoplex Exiprismatorhombated diacosipentacontahexazetton
131											t0,4,5,6{4,3,3,3,3,3,3} Hexipentistericated 8-cube Petitericellated octeract
132											t0,1,4,7{3,3,3,3,3,3,4} Heptisteritruncated 8-orthoplex Exicellitruncated diacosipentacontahexazetton
133											t0,2,4,7{3,3,3,3,3,3,4} Heptistericantellated 8-orthoplex Exicellirhombated diacosipentacontahexazetton
134											t0,3,5,6{4,3,3,3,3,3,3} Hexipentiruncinated 8-cube Petiteriprismated octeract
135											t0,3,4,7{4,3,3,3,3,3,3} Heptisteriruncinated 8-cube Exicelliprismato-octeractidiacosipentacontahexazetton
136											t0,3,4,6{4,3,3,3,3,3,3} Hexisteriruncinated 8-cube Peticelliprismated octeract
137											t0,3,4,5{4,3,3,3,3,3,3} Pentisteriruncinated 8-cube Tericelliprismated octeract
138											t0,1,5,7{3,3,3,3,3,3,4} Heptipentitruncated 8-orthoplex Exiteritruncated diacosipentacontahexazetton
139											t0,2,5,7{4,3,3,3,3,3,3} Heptipenticantellated 8-cube Exiterirhombi-octeractidiacosipentacontahexazetton
140											t0,2,5,6{4,3,3,3,3,3,3} Hexipenticantellated 8-cube Petiterirhombated octeract
141											t0,2,4,7{4,3,3,3,3,3,3} Heptistericantellated 8-cube Exicellirhombated octeract
142											t0,2,4,6{4,3,3,3,3,3,3} Hexistericantellated 8-cube Peticellirhombated octeract
143											t0,2,4,5{4,3,3,3,3,3,3} Pentistericantellated 8-cube Tericellirhombated octeract
144											t0,2,3,7{4,3,3,3,3,3,3} Heptiruncicantellated 8-cube Exiprismatorhombated octeract
145											t0,2,3,6{4,3,3,3,3,3,3} Hexiruncicantellated 8-cube Petiprismatorhombated octeract
146											t0,2,3,5{4,3,3,3,3,3,3} Pentiruncicantellated 8-cube Teriprismatorhombated octeract
147											t0,2,3,4{4,3,3,3,3,3,3} Steriruncicantellated 8-cube Celliprismatorhombated octeract
148											t0,1,6,7{4,3,3,3,3,3,3} Heptihexitruncated 8-cube Exipetitrunki-octeractidiacosipentacontahexazetton
149											t0,1,5,7{4,3,3,3,3,3,3} Heptipentitruncated 8-cube Exiteritruncated octeract
150											t0,1,5,6{4,3,3,3,3,3,3} Hexipentitruncated 8-cube Petiteritruncated octeract
151											t0,1,4,7{4,3,3,3,3,3,3} Heptisteritruncated 8-cube Exicellitruncated octeract
152											t0,1,4,6{4,3,3,3,3,3,3} Hexisteritruncated 8-cube Peticellitruncated octeract
153											t0,1,4,5{4,3,3,3,3,3,3} Pentisteritruncated 8-cube Tericellitruncated octeract
154											t0,1,3,7{4,3,3,3,3,3,3} Heptiruncitruncated 8-cube Exiprismatotruncated octeract
155											t0,1,3,6{4,3,3,3,3,3,3} Hexiruncitruncated 8-cube Petiprismatotruncated octeract
156											t0,1,3,5{4,3,3,3,3,3,3} Pentiruncitruncated 8-cube Teriprismatotruncated octeract
157											t0,1,3,4{4,3,3,3,3,3,3} Steriruncitruncated 8-cube Celliprismatotruncated octeract
158											t0,1,2,7{4,3,3,3,3,3,3} Hepticantitruncated 8-cube Exigreatorhombated octeract
159											t0,1,2,6{4,3,3,3,3,3,3} Hexicantitruncated 8-cube Petigreatorhombated octeract
160											t0,1,2,5{4,3,3,3,3,3,3} Penticantitruncated 8-cube Terigreatorhombated octeract
161											t0,1,2,4{4,3,3,3,3,3,3} Stericantitruncated 8-cube Celligreatorhombated octeract
162											t0,1,2,3{4,3,3,3,3,3,3} Runcicantitruncated 8-cube Great prismated octeract
163											t0,1,2,3,4{3,3,3,3,3,3,4} Steriruncicantitruncated 8-orthoplex Great cellated diacosipentacontahexazetton
164											t0,1,2,3,5{3,3,3,3,3,3,4} Pentiruncicantitruncated 8-orthoplex Terigreatoprismated diacosipentacontahexazetton
165											t0,1,2,4,5{3,3,3,3,3,3,4} Pentistericantitruncated 8-orthoplex Tericelligreatorhombated diacosipentacontahexazetton
166											t0,1,3,4,5{3,3,3,3,3,3,4} Pentisteriruncitruncated 8-orthoplex Tericelliprismatotruncated diacosipentacontahexazetton
167											t0,2,3,4,5{3,3,3,3,3,3,4} Pentisteriruncicantellated 8-orthoplex Tericelliprismatorhombated diacosipentacontahexazetton
168											t1,2,3,4,5{3,3,3,3,3,3,4} Bisteriruncicantitruncated 8-orthoplex Great bicellated diacosipentacontahexazetton
169											t0,1,2,3,6{3,3,3,3,3,3,4} Hexiruncicantitruncated 8-orthoplex Petigreatoprismated diacosipentacontahexazetton
170											t0,1,2,4,6{3,3,3,3,3,3,4} Hexistericantitruncated 8-orthoplex Peticelligreatorhombated diacosipentacontahexazetton
171											t0,1,3,4,6{3,3,3,3,3,3,4} Hexisteriruncitruncated 8-orthoplex Peticelliprismatotruncated diacosipentacontahexazetton
172											t0,2,3,4,6{3,3,3,3,3,3,4} Hexisteriruncicantellated 8-orthoplex Peticelliprismatorhombated diacosipentacontahexazetton
173											t1,2,3,4,6{3,3,3,3,3,3,4} Bipentiruncicantitruncated 8-orthoplex Biterigreatoprismated diacosipentacontahexazetton
174											t0,1,2,5,6{3,3,3,3,3,3,4} Hexipenticantitruncated 8-orthoplex Petiterigreatorhombated diacosipentacontahexazetton
175											t0,1,3,5,6{3,3,3,3,3,3,4} Hexipentiruncitruncated 8-orthoplex Petiteriprismatotruncated diacosipentacontahexazetton
176											t0,2,3,5,6{3,3,3,3,3,3,4} Hexipentiruncicantellated 8-orthoplex Petiteriprismatorhombated diacosipentacontahexazetton
177											t1,2,3,5,6{3,3,3,3,3,3,4} Bipentistericantitruncated 8-orthoplex Bitericelligreatorhombated diacosipentacontahexazetton
178											t0,1,4,5,6{3,3,3,3,3,3,4} Hexipentisteritruncated 8-orthoplex Petitericellitruncated diacosipentacontahexazetton
179											t0,2,4,5,6{3,3,3,3,3,3,4} Hexipentistericantellated 8-orthoplex Petitericellirhombated diacosipentacontahexazetton
180											t1,2,3,5,6{4,3,3,3,3,3,3} Bipentistericantitruncated 8-cube Bitericelligreatorhombated octeract
181											t0,3,4,5,6{3,3,3,3,3,3,4} Hexipentisteriruncinated 8-orthoplex Petitericelliprismated diacosipentacontahexazetton
182											t1,2,3,4,6{4,3,3,3,3,3,3} Bipentiruncicantitruncated 8-cube Biterigreatoprismated octeract
183											t1,2,3,4,5{4,3,3,3,3,3,3} Bisteriruncicantitruncated 8-cube Great bicellated octeract
184											t0,1,2,3,7{3,3,3,3,3,3,4} Heptiruncicantitruncated 8-orthoplex Exigreatoprismated diacosipentacontahexazetton
185											t0,1,2,4,7{3,3,3,3,3,3,4} Heptistericantitruncated 8-orthoplex Exicelligreatorhombated diacosipentacontahexazetton
186											t0,1,3,4,7{3,3,3,3,3,3,4} Heptisteriruncitruncated 8-orthoplex Exicelliprismatotruncated diacosipentacontahexazetton
187											t0,2,3,4,7{3,3,3,3,3,3,4} Heptisteriruncicantellated 8-orthoplex Exicelliprismatorhombated diacosipentacontahexazetton
188											t0,3,4,5,6{4,3,3,3,3,3,3} Hexipentisteriruncinated 8-cube Petitericelliprismated octeract
189											t0,1,2,5,7{3,3,3,3,3,3,4} Heptipenticantitruncated 8-orthoplex Exiterigreatorhombated diacosipentacontahexazetton
190											t0,1,3,5,7{3,3,3,3,3,3,4} Heptipentiruncitruncated 8-orthoplex Exiteriprismatotruncated diacosipentacontahexazetton
191											t0,2,3,5,7{3,3,3,3,3,3,4} Heptipentiruncicantellated 8-orthoplex Exiteriprismatorhombated diacosipentacontahexazetton
192											t0,2,4,5,6{4,3,3,3,3,3,3} Hexipentistericantellated 8-cube Petitericellirhombated octeract
193											t0,1,4,5,7{3,3,3,3,3,3,4} Heptipentisteritruncated 8-orthoplex Exitericellitruncated diacosipentacontahexazetton
194											t0,2,3,5,7{4,3,3,3,3,3,3} Heptipentiruncicantellated 8-cube Exiteriprismatorhombated octeract
195											t0,2,3,5,6{4,3,3,3,3,3,3} Hexipentiruncicantellated 8-cube Petiteriprismatorhombated octeract
196											t0,2,3,4,7{4,3,3,3,3,3,3} Heptisteriruncicantellated 8-cube Exicelliprismatorhombated octeract
197											t0,2,3,4,6{4,3,3,3,3,3,3} Hexisteriruncicantellated 8-cube Peticelliprismatorhombated octeract
198											t0,2,3,4,5{4,3,3,3,3,3,3} Pentisteriruncicantellated 8-cube Tericelliprismatorhombated octeract
199											t0,1,2,6,7{3,3,3,3,3,3,4} Heptihexicantitruncated 8-orthoplex Exipetigreatorhombated diacosipentacontahexazetton
200											t0,1,3,6,7{3,3,3,3,3,3,4} Heptihexiruncitruncated 8-orthoplex Exipetiprismatotruncated diacosipentacontahexazetton
201											t0,1,4,5,7{4,3,3,3,3,3,3} Heptipentisteritruncated 8-cube Exitericellitruncated octeract
202											t0,1,4,5,6{4,3,3,3,3,3,3} Hexipentisteritruncated 8-cube Petitericellitruncated octeract
203											t0,1,3,6,7{4,3,3,3,3,3,3} Heptihexiruncitruncated 8-cube Exipetiprismatotruncated octeract
204											t0,1,3,5,7{4,3,3,3,3,3,3} Heptipentiruncitruncated 8-cube Exiteriprismatotruncated octeract
205											t0,1,3,5,6{4,3,3,3,3,3,3} Hexipentiruncitruncated 8-cube Petiteriprismatotruncated octeract
206											t0,1,3,4,7{4,3,3,3,3,3,3} Heptisteriruncitruncated 8-cube Exicelliprismatotruncated octeract
207											t0,1,3,4,6{4,3,3,3,3,3,3} Hexisteriruncitruncated 8-cube Peticelliprismatotruncated octeract
208											t0,1,3,4,5{4,3,3,3,3,3,3} Pentisteriruncitruncated 8-cube Tericelliprismatotruncated octeract
209											t0,1,2,6,7{4,3,3,3,3,3,3} Heptihexicantitruncated 8-cube Exipetigreatorhombated octeract
210											t0,1,2,5,7{4,3,3,3,3,3,3} Heptipenticantitruncated 8-cube Exiterigreatorhombated octeract
211											t0,1,2,5,6{4,3,3,3,3,3,3} Hexipenticantitruncated 8-cube Petiterigreatorhombated octeract
212											t0,1,2,4,7{4,3,3,3,3,3,3} Heptistericantitruncated 8-cube Exicelligreatorhombated octeract
213											t0,1,2,4,6{4,3,3,3,3,3,3} Hexistericantitruncated 8-cube Peticelligreatorhombated octeract
214											t0,1,2,4,5{4,3,3,3,3,3,3} Pentistericantitruncated 8-cube Tericelligreatorhombated octeract
215											t0,1,2,3,7{4,3,3,3,3,3,3} Heptiruncicantitruncated 8-cube Exigreatoprismated octeract
216											t0,1,2,3,6{4,3,3,3,3,3,3} Hexiruncicantitruncated 8-cube Petigreatoprismated octeract
217											t0,1,2,3,5{4,3,3,3,3,3,3} Pentiruncicantitruncated 8-cube Terigreatoprismated octeract
218											t0,1,2,3,4{4,3,3,3,3,3,3} Steriruncicantitruncated 8-cube Great cellated octeract
219											t0,1,2,3,4,5{3,3,3,3,3,3,4} Pentisteriruncicantitruncated 8-orthoplex Great terated diacosipentacontahexazetton
220											t0,1,2,3,4,6{3,3,3,3,3,3,4} Hexisteriruncicantitruncated 8-orthoplex Petigreatocellated diacosipentacontahexazetton
221											t0,1,2,3,5,6{3,3,3,3,3,3,4} Hexipentiruncicantitruncated 8-orthoplex Petiterigreatoprismated diacosipentacontahexazetton
222											t0,1,2,4,5,6{3,3,3,3,3,3,4} Hexipentistericantitruncated 8-orthoplex Petitericelligreatorhombated diacosipentacontahexazetton
223											t0,1,3,4,5,6{3,3,3,3,3,3,4} Hexipentisteriruncitruncated 8-orthoplex Petitericelliprismatotruncated diacosipentacontahexazetton
224											t0,2,3,4,5,6{3,3,3,3,3,3,4} Hexipentisteriruncicantellated 8-orthoplex Petitericelliprismatorhombated diacosipentacontahexazetton
225											t1,2,3,4,5,6{4,3,3,3,3,3,3} Bipentisteriruncicantitruncated 8-cube Great biteri-octeractidiacosipentacontahexazetton
226											t0,1,2,3,4,7{3,3,3,3,3,3,4} Heptisteriruncicantitruncated 8-orthoplex Exigreatocellated diacosipentacontahexazetton
227											t0,1,2,3,5,7{3,3,3,3,3,3,4} Heptipentiruncicantitruncated 8-orthoplex Exiterigreatoprismated diacosipentacontahexazetton
228											t0,1,2,4,5,7{3,3,3,3,3,3,4} Heptipentistericantitruncated 8-orthoplex Exitericelligreatorhombated diacosipentacontahexazetton
229											t0,1,3,4,5,7{3,3,3,3,3,3,4} Heptipentisteriruncitruncated 8-orthoplex Exitericelliprismatotruncated diacosipentacontahexazetton
230											t0,2,3,4,5,7{4,3,3,3,3,3,3} Heptipentisteriruncicantellated 8-cube Exitericelliprismatorhombi-octeractidiacosipentacontahexazetton
231											t0,2,3,4,5,6{4,3,3,3,3,3,3} Hexipentisteriruncicantellated 8-cube Petitericelliprismatorhombated octeract
232											t0,1,2,3,6,7{3,3,3,3,3,3,4} Heptihexiruncicantitruncated 8-orthoplex Exipetigreatoprismated diacosipentacontahexazetton
233											t0,1,2,4,6,7{3,3,3,3,3,3,4} Heptihexistericantitruncated 8-orthoplex Exipeticelligreatorhombated diacosipentacontahexazetton
234											t0,1,3,4,6,7{4,3,3,3,3,3,3} Heptihexisteriruncitruncated 8-cube Exipeticelliprismatotrunki-octeractidiacosipentacontahexazetton
235											t0,1,3,4,5,7{4,3,3,3,3,3,3} Heptipentisteriruncitruncated 8-cube Exitericelliprismatotruncated octeract
236											t0,1,3,4,5,6{4,3,3,3,3,3,3} Hexipentisteriruncitruncated 8-cube Petitericelliprismatotruncated octeract
237											t0,1,2,5,6,7{4,3,3,3,3,3,3} Heptihexipenticantitruncated 8-cube Exipetiterigreatorhombi-octeractidiacosipentacontahexazetton
238											t0,1,2,4,6,7{4,3,3,3,3,3,3} Heptihexistericantitruncated 8-cube Exipeticelligreatorhombated octeract
239											t0,1,2,4,5,7{4,3,3,3,3,3,3} Heptipentistericantitruncated 8-cube Exitericelligreatorhombated octeract
240											t0,1,2,4,5,6{4,3,3,3,3,3,3} Hexipentistericantitruncated 8-cube Petitericelligreatorhombated octeract
241											t0,1,2,3,6,7{4,3,3,3,3,3,3} Heptihexiruncicantitruncated 8-cube Exipetigreatoprismated octeract
242											t0,1,2,3,5,7{4,3,3,3,3,3,3} Heptipentiruncicantitruncated 8-cube Exiterigreatoprismated octeract
243											t0,1,2,3,5,6{4,3,3,3,3,3,3} Hexipentiruncicantitruncated 8-cube Petiterigreatoprismated octeract
244											t0,1,2,3,4,7{4,3,3,3,3,3,3} Heptisteriruncicantitruncated 8-cube Exigreatocellated octeract
245											t0,1,2,3,4,6{4,3,3,3,3,3,3} Hexisteriruncicantitruncated 8-cube Petigreatocellated octeract
246											t0,1,2,3,4,5{4,3,3,3,3,3,3} Pentisteriruncicantitruncated 8-cube Great terated octeract
247											t0,1,2,3,4,5,6{3,3,3,3,3,3,4} Hexipentisteriruncicantitruncated 8-orthoplex Great petated diacosipentacontahexazetton
248											t0,1,2,3,4,5,7{3,3,3,3,3,3,4} Heptipentisteriruncicantitruncated 8-orthoplex Exigreatoterated diacosipentacontahexazetton
249											t0,1,2,3,4,6,7{3,3,3,3,3,3,4} Heptihexisteriruncicantitruncated 8-orthoplex Exipetigreatocellated diacosipentacontahexazetton
250											t0,1,2,3,5,6,7{3,3,3,3,3,3,4} Heptihexipentiruncicantitruncated 8-orthoplex Exipetiterigreatoprismated diacosipentacontahexazetton
251											t0,1,2,3,5,6,7{4,3,3,3,3,3,3} Heptihexipentiruncicantitruncated 8-cube Exipetiterigreatoprismated octeract
252											t0,1,2,3,4,6,7{4,3,3,3,3,3,3} Heptihexisteriruncicantitruncated 8-cube Exipetigreatocellated octeract
253											t0,1,2,3,4,5,7{4,3,3,3,3,3,3} Heptipentisteriruncicantitruncated 8-cube Exigreatoterated octeract
254											t0,1,2,3,4,5,6{4,3,3,3,3,3,3} Hexipentisteriruncicantitruncated 8-cube Great petated octeract
255											t0,1,2,3,4,5,6,7{4,3,3,3,3,3,3} Omnitruncated 8-cube Great exi-octeractidiacosipentacontahexazetton
256											h0{4,3,3,3,3,3,3} 8-demicube Hemiocteract

References

• Klitzing, Richard. "8D uniform polytopes (polyzetta)".