8-demicube

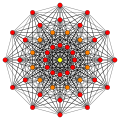
In geometry, a demiocteract or 8-demicube is a uniform 8-polytope, constructed from the 8-hypercube, octeract, with alternated vertices removed. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.

Demiocteract (8-demicube)
Petrie polygon projection
Type	Uniform 8-polytope
Family	demihypercube
Coxeter symbol	151
Schläfli symbols	{3,35,1} = h{4,36} s{21,1,1,1,1,1,1}
Coxeter diagrams	=
7-faces	144: 16 {31,4,1} 128 {36}
6-faces	112 {31,3,1} 1024 {35}
5-faces	448 {31,2,1} 3584 {34}
4-faces	1120 {31,1,1} 7168 {3,3,3}
Cells	10752: 1792 {31,0,1} 8960 {3,3}
Faces	7168 {3}
Edges	1792
Vertices	128
Vertex figure	Rectified 7-simplex
Symmetry group	D8, [35,1,1] = [1+,4,36] A18, [27]+
Dual	?
Properties	convex

E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as HM₈ for an 8-dimensional half measure polytope.

Coxeter named this polytope as 1₅₁ from its Coxeter diagram, with a ring on one of the 1-length branches, and Schläfli symbol ${\displaystyle \left\{3{\begin{array}{l}3,3,3,3,3\\3\end{array}}\right\}}$ or {3,3^5,1}.

Acronym: hocto (Jonathan Bowers)^[1]

Cartesian coordinates

Cartesian coordinates for the vertices of an 8-demicube centered at the origin are alternate halves of the 8-cube:

(±1,±1,±1,±1,±1,±1,±1,±1)

with an odd number of plus signs.

Related polytopes and honeycombs

This polytope is the vertex figure for the uniform tessellation, 2₅₁ with Coxeter-Dynkin diagram:

Images

orthographic projections

Coxeter plane	B8	D8	D7	D6	D5
Graph
Dihedral symmetry	[16/2]	[14]	[12]	[10]	[8]
Coxeter plane	D4	D3	A7	A5	A3
Graph
Dihedral symmetry	[6]	[4]	[8]	[6]	[4]