Mittag-Leffler function

Not to be confused with Mittag-Leffler polynomials.

In mathematics, the Mittag-Leffler functions are a family of special functions. They are complex-valued functions of a complex argument z, and moreover depend on one or two complex parameters.

The Mittag-Leffler function can be used to interpolate continuously between a Gaussian and a Lorentzian function.

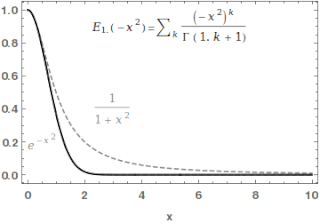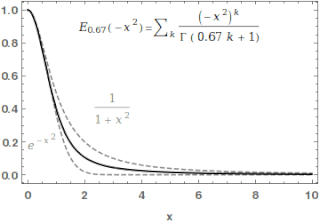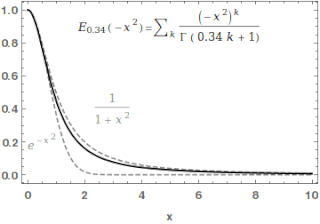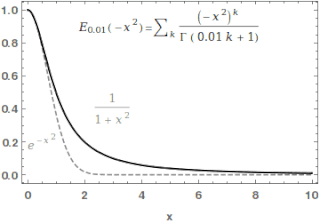
The one-parameter Mittag-Leffler function, introduced by Gösta Mittag-Leffler in 1903,^[1][2] can be defined by the Maclaurin series

${\displaystyle E_{\alpha }(z)=\sum _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (\alpha k+1)}},}$

where ${\displaystyle \Gamma (x)}$ is the gamma function, and ${\displaystyle \alpha }$ is a complex parameter with ${\displaystyle \operatorname {Re} \left(\alpha \right)>0}$.

The two-parameter Mittag-Leffler function, introduced by Wiman in 1905,^[3][2] is occasionally called the generalized Mittag-Leffler function. It has an additional complex parameter ${\displaystyle \beta }$, and may be defined by the series^[2][4]

${\displaystyle E_{\alpha ,\beta }(z)=\sum _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (\alpha k+\beta )}},}$

When ${\displaystyle \beta =1}$, the one-parameter function ${\displaystyle E_{\alpha }=E_{\alpha ,1}}$ is recovered.

In the case ${\displaystyle \alpha }$ and ${\displaystyle \beta }$ are real and positive, the series converges for all values of the argument ${\displaystyle z}$, so the Mittag-Leffler function is an entire function. This class of functions are important in the theory of the fractional calculus.

See below for three-parameter generalizations.

Some basic properties

For ${\displaystyle \alpha >0}$, the Mittag-Leffler function ${\displaystyle E_{\alpha ,\beta }(z)}$ is an entire function of order ${\displaystyle 1/\alpha }$, and type ${\displaystyle 1}$ for any value of ${\displaystyle \beta }$. In some sense, the Mittag-Leffler function is the simplest entire function of its order. The indicator function of ${\displaystyle E_{\alpha }(z)}$ is^[5]: 50 $${\displaystyle h_{E_{\alpha }}(\theta )={\begin{cases}\cos \left({\frac {\theta }{\alpha }}\right),&{\text{for }}|\theta |\leq {\frac {1}{2}}\alpha \pi$$ ;\\0,&{\text{otherwise}}.\end{cases}}} This result actually holds for ${\displaystyle \beta \neq 1}$ as well with some restrictions on ${\displaystyle \beta }$ when ${\displaystyle \alpha =1}$.^[6]: 67

The Mittag-Leffler function satisfies the recurrence property (Theorem 5.1 of ^[2])

${\displaystyle E_{\alpha ,\beta }(z)={\frac {1}{z}}E_{\alpha ,\beta -\alpha }(z)-{\frac {1}{z\Gamma (\beta -\alpha )}},}$

from which the following asymptotic expansion holds : for ${\displaystyle 0<\alpha <2}$ and ${\displaystyle \mu }$ real such that ${\displaystyle {\frac {\pi \alpha }{2}}<\mu <\min(\pi ,\pi \alpha )}$ then for all ${\displaystyle N\in \mathbb {N} ^{*},N\neq 1}$, we can show the following asymptotic expansions (Section 6. of ^[2]):

-as ${\displaystyle \,|z|\to +\infty ,|{\text{arg}}(z)|\leq \mu }$:

${\displaystyle E_{\alpha }(z)={\frac {1}{\alpha }}\exp(z^{\frac {1}{\alpha }})-\sum \limits _{k=1}^{N}{\frac {1}{z^{k}\,\Gamma (1-\alpha k)}}+O\left({\frac {1}{z^{N+1}}}\right)}$,

-and as ${\displaystyle \,|z|\to +\infty ,\mu \leq |{\text{arg}}(z)|\leq \pi }$:

${\displaystyle E_{\alpha }(z)=-\sum \limits _{k=1}^{N}{\frac {1}{z^{k}\Gamma (1-\alpha k)}}+O\left({\frac {1}{z^{N+1}}}\right)}$.

A simpler estimate that can often be useful is given, thanks to the fact that the order and type of ${\displaystyle E_{\alpha ,\beta }(z)}$ is ${\displaystyle 1/\alpha }$ and ${\displaystyle 1}$, respectively:^[6]: 62

${\displaystyle |E_{\alpha ,\beta }(z)|\leq C\exp \left(\sigma |z|^{1/\alpha }\right)}$

for any positive ${\displaystyle C}$ and any ${\displaystyle \sigma >1}$.

Special cases

For ${\displaystyle \alpha =0}$, the series above equals the Taylor expansion of the geometric series and consequently ${\displaystyle E_{0,\beta }(z)={\frac {1}{\Gamma (\beta )}}{\frac {1}{1-z}}}$.

For ${\displaystyle \alpha =1/2,1,2}$ we find: (Section 2 of ^[2])

Error function:

${\displaystyle E_{\frac {1}{2}}(z)=\exp(z^{2})\operatorname {erfc} (-z).}$

Exponential function:

${\displaystyle E_{1}(z)=\sum _{k=0}^{\infty }{\frac {z^{k}}{\Gamma (k+1)}}=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}=\exp(z).}$

Hyperbolic cosine:

${\displaystyle E_{2}(z)=\cosh({\sqrt {z}}),{\text{ and }}E_{2}(-z^{2})=\cos(z).}$

For ${\displaystyle \beta =2}$, we have

${\displaystyle E_{1,2}(z)={\frac {e^{z}-1}{z}},}$

${\displaystyle E_{2,2}(z)={\frac {\sinh({\sqrt {z}})}{\sqrt {z}}}.}$

For ${\displaystyle \alpha =0,1,2}$, the integral

${\displaystyle \int _{0}^{z}E_{\alpha }(-s^{2})\,{\mathrm {d} }s}$

gives, respectively: ${\displaystyle \arctan(z)}$, ${\displaystyle {\tfrac {\sqrt {\pi }}{2}}\operatorname {erf} (z)}$, ${\displaystyle \sin(z)}$.

Mittag-Leffler's integral representation

The integral representation of the Mittag-Leffler function is (Section 6 of ^[2])

${\displaystyle E_{\alpha ,\beta }(z)={\frac {1}{2\pi i}}\oint _{C}{\frac {t^{\alpha -\beta }e^{t}}{t^{\alpha }-z}}\,dt,\Re (\alpha )>0,\Re (\beta )>0,}$

where the contour ${\displaystyle C}$ starts and ends at ${\displaystyle -\infty }$ and circles around the singularities and branch points of the integrand.

Related to the Laplace transform and Mittag-Leffler summation is the expression (Eq (7.5) of ^[2] with ${\displaystyle m=0}$)

${\displaystyle \int _{0}^{\infty }e^{-tz}t^{\beta -1}E_{\alpha ,\beta }(\pm r\,t^{\alpha })\,dt={\frac {z^{\alpha -\beta }}{z^{\alpha }\mp r}},\Re (z)>0,\Re (\alpha )>0,\Re (\beta )>0.}$

Three-parameter generalizations

One generalization, characterized by three parameters, is

${\displaystyle E_{\alpha ,\beta }^{\gamma }(z)=\left({\frac {1}{\Gamma (\gamma )}}\right)\sum \limits _{k=1}^{\infty }{\frac {\Gamma (\gamma +k)z^{k}}{k!\Gamma (\alpha k+\beta )}},}$

where ${\displaystyle \alpha ,\beta }$ and ${\displaystyle \gamma }$ are complex parameters and ${\displaystyle \Re (\alpha )>0}$.^[6]

Another generalization is the Prabhakar function

${\displaystyle E_{\alpha ,\beta }^{\gamma }(z)=\sum _{k=0}^{\infty }{\frac {(\gamma )_{k}z^{k}}{k!\Gamma (\alpha k+\beta )}},}$

where ${\displaystyle (\gamma )_{k}}$ is the Pochhammer symbol.

Applications of Mittag-Leffler function

One of the applications of the Mittag-Leffler function is in modeling fractional order viscoelastic materials. Experimental investigations into the time-dependent relaxation behavior of viscoelastic materials are characterized by a very fast decrease of the stress at the beginning of the relaxation process and an extremely slow decay for large times, i.e. it takes a long time to approach a constant asymptotic value. Therefore, many Maxwell elements are required to describe relaxation behavior to sufficient accuracy. This results in a difficult optimization problem in order to identify the large number of material parameters required. On the other hand, over the years, the concept of fractional derivatives has been introduced into the theory of viscoelasticity. Among these models, the fractional Zener model was found to be very effective for predicting the dynamic nature of rubber-like materials using only a small number of material parameters. The solution of the corresponding constitutive equation leads to a relaxation function of the Mittag-Leffler type. It is defined by the power series with negative arguments. This function represents all essential properties of the relaxation process under the influence of an arbitrary and continuous signal with a jump at the origin.^[7][8]

See also

• Mittag-Leffler summation
• Mittag-Leffler distribution

Notes

• R Package 'MittagLeffleR' by Gurtek Gill, Peter Straka. Implements the Mittag-Leffler function, distribution, random variate generation, and estimation.