Top Qs
Timeline
Chat
Perspective
Monotonic function
Order-preserving mathematical function From Wikipedia, the free encyclopedia
Remove ads
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order.[1][2][3] This concept first arose in calculus, and was later generalized to the more abstract setting of order theory.

Remove ads
In calculus and analysis
Summarize
Perspective
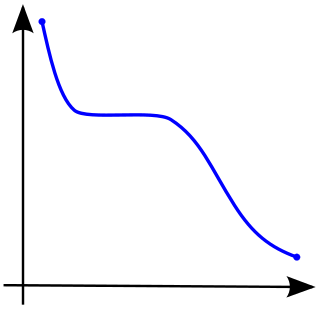
In calculus, a function defined on a subset of the real numbers with real values is called monotonic if it is either entirely non-decreasing, or entirely non-increasing.[2] That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease.
A function is termed monotonically increasing (also increasing or non-decreasing)[3] if for all and such that one has , so preserves the order (see Figure 1). Likewise, a function is called monotonically decreasing (also decreasing or non-increasing)[3] if, whenever , then , so it reverses the order (see Figure 2).
If the order in the definition of monotonicity is replaced by the strict order , one obtains a stronger requirement. A function with this property is called strictly increasing (also increasing).[3][4] Again, by inverting the order symbol, one finds a corresponding concept called strictly decreasing (also decreasing).[3][4] A function with either property is called strictly monotone. Functions that are strictly monotone are one-to-one (because for not equal to , either or and so, by monotonicity, either or , thus .
To avoid ambiguity, the terms weakly monotone, weakly increasing and weakly decreasing are often used to refer to non-strict monotonicity.
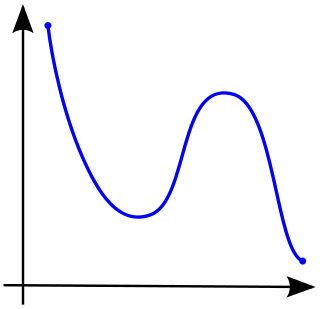
The terms "non-decreasing" and "non-increasing" should not be confused with the (much weaker) negative qualifications "not decreasing" and "not increasing". For example, the non-monotonic function shown in figure 3 first falls, then rises, then falls again. It is therefore not decreasing and not increasing, but it is neither non-decreasing nor non-increasing.
A function is said to be absolutely monotonic over an interval if the derivatives of all orders of are nonnegative or all nonpositive at all points on the interval.
Inverse of function
All strictly monotonic functions are invertible because they are guaranteed to have a one-to-one mapping from their range to their domain.
However, functions that are only weakly monotone need not be invertible; they may be constant on some interval (and therefore not one-to-one).
A function may be strictly monotonic over a limited a range of values and thus have an inverse on that range even though it is not strictly monotonic everywhere. For example, if is strictly increasing on the range , then it has an inverse on the range .
The term monotonic is sometimes used in place of strictly monotonic, so a source may state that all monotonic functions are invertible when they really mean that all strictly monotonic functions are invertible.[citation needed]
Monotonic transformation
The term monotonic transformation (or monotone transformation) may also cause confusion because it refers to a transformation by a strictly increasing function. This is the case in economics with respect to the ordinal properties of a utility function being preserved across a monotonic transform (see also monotone preferences).[5] In this context, the term "monotonic transformation" refers to a positive monotonic transformation and is intended to distinguish it from a "negative monotonic transformation," which reverses the order of the numbers.[6]
Some basic applications and results


The following properties are true for a monotonic function :
- has limits from the right and from the left at every point of its domain;
- has a limit at positive or negative infinity () of either a real number, , or .
- can only have jump and removable discontinuities.
- can only have countably many discontinuities in its domain. The discontinuities, however, do not necessarily consist of isolated points and may even be dense in an interval (a, b). For example, for any summable sequence of positive numbers and any enumeration of the rational numbers, the monotonically increasing function is continuous exactly at every irrational number (cf. picture). It is the cumulative distribution function of the discrete measure on the rational numbers, where is the weight of .
- If is differentiable at and , then there is a non-degenerate interval I such that and is increasing on I. As a partial converse, if f is differentiable and increasing on an interval, I, then its derivative is positive at every point in I.
These properties are the reason why monotonic functions are useful in technical work in analysis. Other important properties of these functions include:
- if is a monotonic function defined on an interval , then is differentiable almost everywhere on ; i.e. the set of numbers in such that is not differentiable in has Lebesgue measure zero. In addition, this result cannot be improved to countable: see Cantor function.
- if this set is countable, then is absolutely continuous
- if is a monotonic function defined on an interval , then is Riemann integrable.
An important application of monotonic functions is in probability theory. If is a random variable, its cumulative distribution function is a monotonically increasing function.
A function is unimodal if it is monotonically increasing up to some point (the mode) and then monotonically decreasing.
When is a strictly monotonic function, then is injective on its domain, and if is the range of , then there is an inverse function on for . In contrast, each constant function is monotonic, but not injective,[7] and hence cannot have an inverse.
The graphic shows six monotonic functions. Their simplest forms are shown in the plot area and the expressions used to create them are shown on the y-axis.
Remove ads
In topology
A map is said to be monotone if each of its fibers is connected; that is, for each element the (possibly empty) set is a connected subspace of
Remove ads
In functional analysis
In functional analysis on a topological vector space , a (possibly non-linear) operator is said to be a monotone operator if
Kachurovskii's theorem shows that convex functions on Banach spaces have monotonic operators as their derivatives.
A subset of is said to be a monotone set if for every pair and in ,
is said to be maximal monotone if it is maximal among all monotone sets in the sense of set inclusion. The graph of a monotone operator is a monotone set. A monotone operator is said to be maximal monotone if its graph is a maximal monotone set.
Remove ads
In order theory
Summarize
Perspective
Order theory deals with arbitrary partially ordered sets and preordered sets as a generalization of real numbers. The above definition of monotonicity is relevant in these cases as well. However, the terms "increasing" and "decreasing" are avoided, since their conventional pictorial representation does not apply to orders that are not total. Furthermore, the strict relations and are of little use in many non-total orders and hence no additional terminology is introduced for them.
Letting denote the partial order relation of any partially ordered set, a monotone function, also called isotone, or order-preserving, satisfies the property
for all x and y in its domain. The composite of two monotone mappings is also monotone.
The dual notion is often called antitone, anti-monotone, or order-reversing. Hence, an antitone function f satisfies the property
for all x and y in its domain.
A constant function is both monotone and antitone; conversely, if f is both monotone and antitone, and if the domain of f is a lattice, then f must be constant.
Monotone functions are central in order theory. They appear in most articles on the subject and examples from special applications are found in these places. Some notable special monotone functions are order embeddings (functions for which if and only if and order isomorphisms (surjective order embeddings).
Remove ads
In the context of search algorithms
Summarize
Perspective
In the context of search algorithms monotonicity (also called consistency) is a condition applied to heuristic functions. A heuristic is monotonic if, for every node n and every successor n' of n generated by any action a, the estimated cost of reaching the goal from n is no greater than the step cost of getting to n' plus the estimated cost of reaching the goal from n',
This is a form of triangle inequality, with n, n', and the goal Gn closest to n. Because every monotonic heuristic is also admissible, monotonicity is a stricter requirement than admissibility. Some heuristic algorithms such as A* can be proven optimal provided that the heuristic they use is monotonic.[8]
Remove ads
In Boolean functions
Summarize
Perspective
 |
 |
In Boolean algebra, a monotonic function is one such that for all ai and bi in {0,1}, if a1 ≤ b1, a2 ≤ b2, ..., an ≤ bn (i.e. the Cartesian product {0, 1}n is ordered coordinatewise), then f(a1, ..., an) ≤ f(b1, ..., bn). In other words, a Boolean function is monotonic if, for every combination of inputs, switching one of the inputs from false to true can only cause the output to switch from false to true and not from true to false. Graphically, this means that an n-ary Boolean function is monotonic when its representation as an n-cube labelled with truth values has no upward edge from true to false. (This labelled Hasse diagram is the dual of the function's labelled Venn diagram, which is the more common representation for n ≤ 3.)
The monotonic Boolean functions are precisely those that can be defined by an expression combining the inputs (which may appear more than once) using only the operators and and or (in particular not is forbidden). For instance "at least two of a, b, c hold" (the ternary majority function) is a monotonic function of a, b, c, since it can be written for instance as ((a and b) or (a and c) or (b and c)).
The number of such functions on n variables is known as the Dedekind number of n.
SAT solving, generally an NP-hard task, can be achieved efficiently when all involved functions and predicates are monotonic and Boolean.[9]
Remove ads
See also
Notes
Bibliography
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
















![{\displaystyle [a,b]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle [g(a),g(b)]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/091dac07a170589d4ed7e965623e55d374a9de23)













![{\displaystyle \left[a,b\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)











![{\displaystyle [u_{1},w_{1}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/42f2c67bc4887974d491ba4a419dc798ed50d8cd)
![{\displaystyle [u_{2},w_{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/32202d66739c2039a8b74e861330c713a44db704)







