Neovius surface

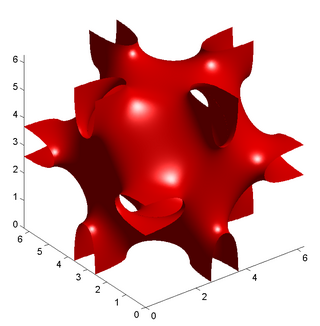
In differential geometry, the Neovius surface is a triply periodic minimal surface originally discovered by Finnish mathematician Edvard Rudolf Neovius (the uncle of Rolf Nevanlinna).^[1][2]

Neovius' minimal surface in a unit cell.

The surface has genus 9, dividing space into two infinite non-equivalent labyrinths. Like many other triply periodic minimal surfaces it has been studied in relation to the microstructure of block copolymers, surfactant-water mixtures,^[3] and crystallography of soft materials.^[4]

It can be approximated with the level set surface^[5]

${\displaystyle 3(\cos x+\cos y+\cos z)+4\cos x\cos y\cos z=0}$

In Schoen's categorisation it is called the C(P) surface, since it is the "complement" of the Schwarz P surface. It can be extended with further handles, converging towards the expanded regular octahedron (in Schoen's categorisation)^[6][7]