Partition of an interval
Increasing sequence of numbers that span an interval From Wikipedia, the free encyclopedia
In mathematics, a partition of an interval [a, b] on the real line is a finite sequence x0, x1, x2, …, xn of real numbers such that
- a = x0 < x1 < x2 < … < xn = b.
In other terms, a partition of a compact interval I is a strictly increasing sequence of numbers (belonging to the interval I itself) starting from the initial point of I and arriving at the final point of I.
Every interval of the form [xi, xi + 1] is referred to as a subinterval of the partition x.
Refinement of a partition
Another partition Q of the given interval [a, b] is defined as a refinement of the partition P, if Q contains all the points of P and possibly some other points as well; the partition Q is said to be “finer” than P. Given two partitions, P and Q, one can always form their common refinement, denoted P ∨ Q, which consists of all the points of P and Q, in increasing order.[1]
Norm of a partition
The norm (or mesh) of the partition
- x0 < x1 < x2 < … < xn
is the length of the longest of these subintervals[2][3]
- max{|xi − xi−1| : i = 1, … , n }.
Applications
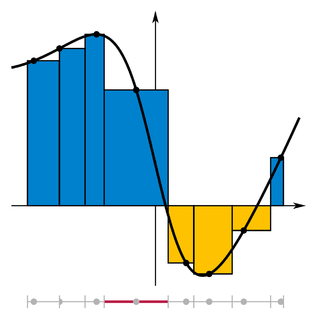
Partitions are used in the theory of the Riemann integral, the Riemann–Stieltjes integral and the regulated integral. Specifically, as finer partitions of a given interval are considered, their mesh approaches zero and the Riemann sum based on a given partition approaches the Riemann integral.[4]
Tagged partitions
A tagged partition or Perron Partition is a partition of a given interval together with a finite sequence of numbers t0, …, tn − 1 subject to the conditions that for each i,
- xi ≤ ti ≤ xi + 1.
In other words, a tagged partition is a partition together with a distinguished point of every subinterval: its mesh is defined in the same way as for an ordinary partition.[5]
See also
References
Further reading
Wikiwand - on
Seamless Wikipedia browsing. On steroids.