Rectangular function

"Box function" redirects here. For the Conway box function, see Minkowski's question-mark function § Conway box function.

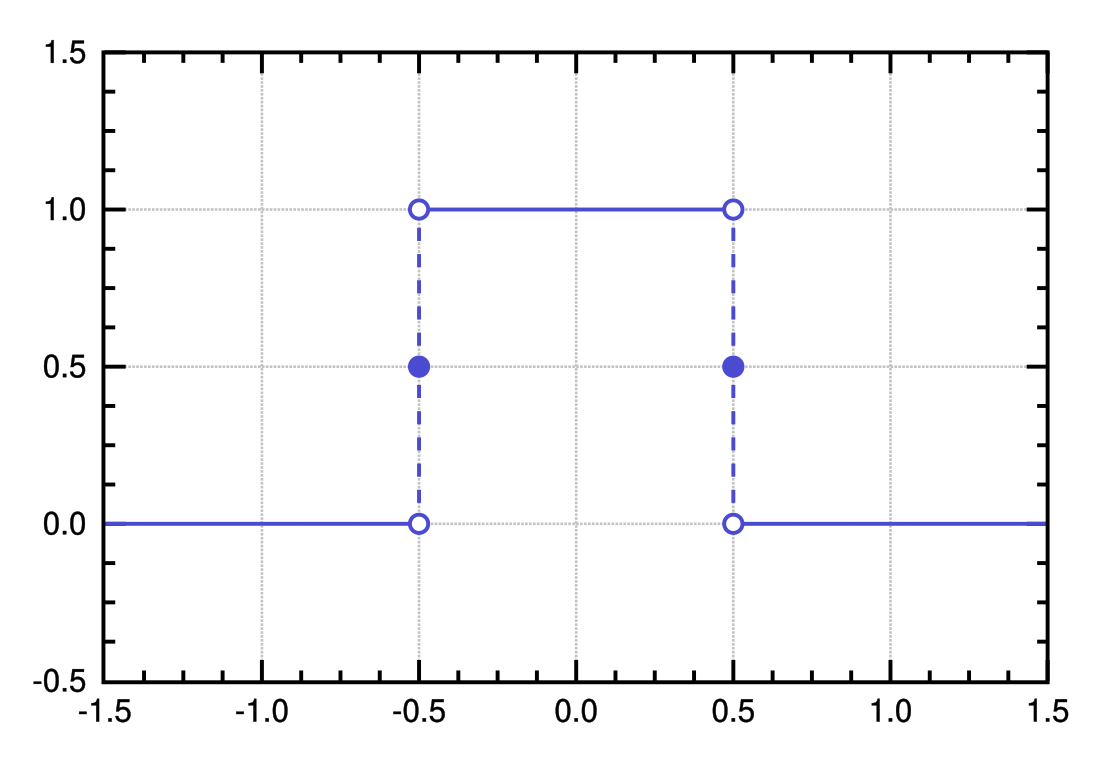
The rectangular function (also known as the rectangle function, rect function, Pi function, Heaviside Pi function,^[1] gate function, unit pulse, or the normalized boxcar function) is defined as^[2]

Rectangular function with a = 1

$${\displaystyle \operatorname {rect} \left({\frac {t}{a}}\right)=\Pi \left({\frac {t}{a}}\right)=\left\{{\begin{array}{rl}0,&{\text{if }}|t|>{\frac {a}{2}}\\{\frac {1}{2}},&{\text{if }}|t|={\frac {a}{2}}\\1,&{\text{if }}|t|<{\frac {a}{2}}.\end{array}}\right.}$$

Alternative definitions of the function define ${\textstyle \operatorname {rect} \left(\pm {\frac {1}{2}}\right)}$ to be 0,^[3] 1,^[4][5] or undefined.

Its periodic version is called a rectangular wave.

History

The rect function has been introduced 1953 by Woodward^[6] in "Probability and Information Theory, with Applications to Radar"^[7] as an ideal cutout operator, together with the sinc function^[8][9] as an ideal interpolation operator, and their counter operations which are sampling (comb operator) and replicating (rep operator), respectively.

Relation to the boxcar function

The rectangular function is a special case of the more general boxcar function:

$${\displaystyle \operatorname {rect} \left({\frac {t-X}{Y}}\right)=H(t-(X-Y/2))-H(t-(X+Y/2))=H(t-X+Y/2)-H(t-X-Y/2)}$$

where ${\displaystyle H(x)}$ is the Heaviside step function; the function is centered at ${\displaystyle X}$ and has duration ${\displaystyle Y}$, from ${\displaystyle X-Y/2}$ to ${\displaystyle X+Y/2.}$

Fourier transform of the rectangular function

Plot of normalized ${\displaystyle \operatorname {sinc} (x)}$ function (i.e. ${\displaystyle \operatorname {sinc} (\pi x)}$) with its spectral frequency components.

The unitary Fourier transforms of the rectangular function are^[2] $${\displaystyle \int _{-\infty }^{\infty }\operatorname {rect} (t)\cdot e^{-i2\pi ft}\,dt={\frac {\sin(\pi f)}{\pi f}}=\operatorname {sinc} _{\pi }(f),}$$ using ordinary frequency f, where ${\displaystyle \operatorname {sinc} _{\pi }}$ is the normalized form^[10] of the sinc function and $${\displaystyle {\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\operatorname {rect} (t)\cdot e^{-i\omega t}\,dt={\frac {1}{\sqrt {2\pi }}}\cdot {\frac {\sin \left(\omega /2\right)}{\omega /2}}={\frac {1}{\sqrt {2\pi }}}\cdot \operatorname {sinc} \left(\omega /2\right),}$$ using angular frequency ${\displaystyle \omega }$, where ${\displaystyle \operatorname {sinc} }$ is the unnormalized form of the sinc function.

For ${\displaystyle \operatorname {rect} (x/a)}$, its Fourier transform is$${\displaystyle \int _{-\infty }^{\infty }\operatorname {rect} \left({\frac {t}{a}}\right)\cdot e^{-i2\pi ft}\,dt=a{\frac {\sin(\pi af)}{\pi af}}=a\ \operatorname {sinc} _{\pi }{(af)}.}$$

Relation to the triangular function

We can define the triangular function as the convolution of two rectangular functions:

$${\displaystyle \operatorname {tri(t/T)} =\operatorname {rect(2t/T)} *\operatorname {rect(2t/T)} .\,}$$

Use in probability

Main article: Uniform distribution (continuous)

Viewing the rectangular function as a probability density function, it is a special case of the continuous uniform distribution with ${\displaystyle a=-1/2,b=1/2.}$ The characteristic function is

$${\displaystyle \varphi (k)={\frac {\sin(k/2)}{k/2}},}$$

and its moment-generating function is

$${\displaystyle M(k)={\frac {\sinh(k/2)}{k/2}},}$$

where ${\displaystyle \sinh(t)}$ is the hyperbolic sine function.

Rational approximation

The pulse function may also be expressed as a limit of a rational function:

$${\displaystyle \Pi (t)=\lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}.}$$

Demonstration of validity

First, we consider the case where ${\textstyle |t|<{\frac {1}{2}}.}$ Notice that the term ${\textstyle (2t)^{2n}}$ is always positive for integer ${\displaystyle n.}$ However, ${\displaystyle 2t<1}$ and hence ${\textstyle (2t)^{2n}}$ approaches zero for large ${\displaystyle n.}$

It follows that: $${\displaystyle \lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}={\frac {1}{0+1}}=1,|t|<{\tfrac {1}{2}}.}$$

Second, we consider the case where ${\textstyle |t|>{\frac {1}{2}}.}$ Notice that the term ${\textstyle (2t)^{2n}}$ is always positive for integer ${\displaystyle n.}$ However, ${\displaystyle 2t>1}$ and hence ${\textstyle (2t)^{2n}}$ grows very large for large ${\displaystyle n.}$

It follows that: $${\displaystyle \lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}={\frac {1}{+\infty +1}}=0,|t|>{\tfrac {1}{2}}.}$$

Third, we consider the case where ${\textstyle |t|={\frac {1}{2}}.}$ We may simply substitute in our equation:

$${\displaystyle \lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}=\lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{1^{2n}+1}}={\frac {1}{1+1}}={\tfrac {1}{2}}.}$$

We see that it satisfies the definition of the pulse function. Therefore,

$${\displaystyle \operatorname {rect} (t)=\Pi (t)=\lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}={\begin{cases}0&{\mbox{if }}|t|>{\frac {1}{2}}\\{\frac {1}{2}}&{\mbox{if }}|t|={\frac {1}{2}}\\1&{\mbox{if }}|t|<{\frac {1}{2}}.\\\end{cases}}}$$

Dirac delta function

The rectangle function can be used to represent the Dirac delta function ${\displaystyle \delta (x)}$.^[11] Specifically,$${\displaystyle \delta (x)=\lim _{a\to 0}{\frac {1}{a}}\operatorname {rect} \left({\frac {x}{a}}\right).}$$For a function ${\displaystyle g(x)}$, its average over the width ${\displaystyle a}$ around 0 in the function domain is calculated as,

$${\displaystyle g_{avg}(0)={\frac {1}{a}}\int \limits _{-\infty }^{\infty }dx\ g(x)\operatorname {rect} \left({\frac {x}{a}}\right).}$$ To obtain ${\displaystyle g(0)}$, the following limit is applied,

$${\displaystyle g(0)=\lim _{a\to 0}{\frac {1}{a}}\int \limits _{-\infty }^{\infty }dx\ g(x)\operatorname {rect} \left({\frac {x}{a}}\right)}$$ and this can be written in terms of the Dirac delta function as, $${\displaystyle g(0)=\int \limits _{-\infty }^{\infty }dx\ g(x)\delta (x).}$$The Fourier transform of the Dirac delta function ${\displaystyle \delta (t)}$ is

$${\displaystyle \delta (f)=\int _{-\infty }^{\infty }\delta (t)\cdot e^{-i2\pi ft}\,dt=\lim _{a\to 0}{\frac {1}{a}}\int _{-\infty }^{\infty }\operatorname {rect} \left({\frac {t}{a}}\right)\cdot e^{-i2\pi ft}\,dt=\lim _{a\to 0}\operatorname {sinc} {(af)}.}$$ where the sinc function here is the normalized sinc function. Because the first zero of the sinc function is at ${\displaystyle f=1/a}$ and ${\displaystyle a}$ goes to infinity, the Fourier transform of ${\displaystyle \delta (t)}$ is

$${\displaystyle \delta (f)=1,}$$ means that the frequency spectrum of the Dirac delta function is infinitely broad. As a pulse is shorten in time, it is larger in spectrum.

See also

• Fourier transform
• Square wave
• Step function
• Top-hat filter
• Boxcar function