Rhombidodecadodecahedron

In geometry, the rhombidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U₃₈. It has 54 faces (30 squares, 12 pentagons and 12 pentagrams), 120 edges and 60 vertices.^[1] It is given a Schläfli symbol t_0,2{5⁄2,5}, and by the Wythoff construction this polyhedron can also be named a cantellated great dodecahedron.

Rhombidodecadodecahedron
Type	Uniform star polyhedron
Elements	F = 54, E = 120 V = 60 (χ = −6)
Faces by sides	30{4}+12{5}+12{5/2}
Coxeter diagram
Wythoff symbol	5/2 5 | 2
Symmetry group	Ih, [5,3], *532
Index references	U38, C48, W76
Dual polyhedron	Medial deltoidal hexecontahedron
Vertex figure	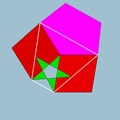4.5/2.4.5
Bowers acronym	Raded

3D model of a rhombidodecadodecahedron

Cartesian coordinates

Cartesian coordinates for the vertices of a uniform great rhombicosidodecahedron are all the even permutations of

(±1/τ², 0, ±τ²)

(±1, ±1, ±√5)

(±2, ±1/τ, ±τ)

where τ = (1+√5)/2 is the golden ratio (sometimes written φ).

Related polyhedra

It shares its vertex arrangement with the uniform compounds of 10 or 20 triangular prisms. It additionally shares its edges with the icosidodecadodecahedron (having the pentagonal and pentagrammic faces in common) and the rhombicosahedron (having the square faces in common).

convex hull	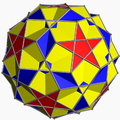Rhombidodecadodecahedron	Icosidodecadodecahedron
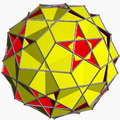Rhombicosahedron	Compound of ten triangular prisms	Compound of twenty triangular prisms

Medial deltoidal hexecontahedron

Medial deltoidal hexecontahedron
Type	Star polyhedron
Face
Elements	F = 60, E = 120 V = 54 (χ = −6)
Symmetry group	Ih, [5,3], *532
Index references	DU38
dual polyhedron	Rhombidodecadodecahedron

3D model of a medial deltoidal hexecontahedron

The medial deltoidal hexecontahedron (or midly lanceal ditriacontahedron) is a nonconvex isohedral polyhedron. It is the dual of the rhombidodecadodecahedron. It has 60 intersecting quadrilateral faces.

See also

• List of uniform polyhedra