Rule of mixtures

In materials science, a general rule of mixtures is a weighted mean used to predict various properties of a composite material .^[1][2][3] It provides a theoretical upper- and lower-bound on properties such as the elastic modulus,^[1] ultimate tensile strength, thermal conductivity, and electrical conductivity.^[3] In general there are two models, the rule of mixtures for axial loading (Voigt model),^[2][4] and the inverse rule of mixtures for transverse loading (Reuss model).^[2][5]

The upper and lower bounds on the elastic modulus of a composite material assuming equal Poisson's coefficients.

For some material property ${\displaystyle E}$, the rule of mixtures states that the overall property in the direction parallel to the fibers could be as high as

${\displaystyle E_{\parallel }=fE_{f}+\left(1-f\right)E_{m}}$

The inverse rule of mixtures states that in the direction perpendicular to the fibers, the elastic modulus of a composite could be as low as

${\displaystyle E_{\perp }=\left({\frac {f}{E_{f}}}+{\frac {1-f}{E_{m}}}\right)^{-1}.}$

where

• ${\displaystyle f={\frac {V_{f}}{V_{f}+V_{m}}}}$ is the volume fraction of the fibers
• ${\displaystyle E_{\parallel }}$ is the material property of the composite parallel to the fibers
• ${\displaystyle E_{\perp }}$ is the material property of the composite perpendicular to the fibers
• ${\displaystyle E_{f}}$ is the material property of the fibers
• ${\displaystyle E_{m}}$ is the material property of the matrix

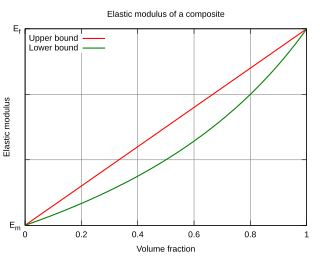
If the property under study is the elastic modulus, these properties are known as the upper-bound modulus, corresponding to loading parallel to the fibers; and the lower-bound modulus, corresponding to transverse loading.^[2]

Derivation for elastic modulus

Rule of mixtures / Voigt model / equal strain

Consider a composite material under uniaxial tension ${\displaystyle \sigma _{\infty }}$. If the material is to stay intact, the strain of the fibers, ${\displaystyle \epsilon _{f}}$ must equal the strain of the matrix, ${\displaystyle \epsilon _{m}}$. Hooke's law for uniaxial tension hence gives

${\displaystyle {\frac {\sigma _{f}}{E_{f}}}=\epsilon _{f}=\epsilon _{m}={\frac {\sigma _{m}}{E_{m}}}}$

1

where ${\displaystyle \sigma _{f}}$, ${\displaystyle E_{f}}$, ${\displaystyle \sigma _{m}}$, ${\displaystyle E_{m}}$ are the stress and elastic modulus of the fibers and the matrix, respectively. Noting stress to be a force per unit area, a force balance gives that

${\displaystyle \sigma _{\infty }=f\sigma _{f}+\left(1-f\right)\sigma _{m}}$

2

where ${\displaystyle f}$ is the volume fraction of the fibers in the composite (and ${\displaystyle 1-f}$ is the volume fraction of the matrix).

If it is assumed that the composite material behaves as a linear-elastic material, i.e., abiding Hooke's law ${\displaystyle \sigma _{\infty }=E_{\parallel }\epsilon _{c}}$ for some elastic modulus of the composite parallel to the fibres ${\displaystyle E_{\parallel }}$ and some strain of the composite ${\displaystyle \epsilon _{c}}$, then equations 1 and 2 can be combined to give

${\displaystyle E_{\parallel }\epsilon _{c}=fE_{f}\epsilon _{f}+\left(1-f\right)E_{m}\epsilon _{m}.}$

Finally, since ${\displaystyle \epsilon _{c}=\epsilon _{f}=\epsilon _{m}}$, the overall elastic modulus of the composite can be expressed as^[6]

${\displaystyle E_{\parallel }=fE_{f}+\left(1-f\right)E_{m}.}$

Assuming the Poisson's ratio of the two materials is the same, this represents the upper bound of the composite's elastic modulus.^[7]

Inverse rule of mixtures / Reuss model / equal stress

Now let the composite material be loaded perpendicular to the fibers, assuming that ${\displaystyle \sigma _{\infty }=\sigma _{f}=\sigma _{m}}$. The overall strain in the composite is distributed between the materials such that

${\displaystyle \epsilon _{c}=f\epsilon _{f}+\left(1-f\right)\epsilon _{m}.}$

The overall modulus in the material is then given by

${\displaystyle E_{\perp }={\frac {\sigma _{\infty }}{\epsilon _{c}}}={\frac {\sigma _{f}}{f\epsilon _{f}+\left(1-f\right)\epsilon _{m}}}=\left({\frac {f}{E_{f}}}+{\frac {1-f}{E_{m}}}\right)^{-1}}$

since ${\displaystyle \sigma _{f}=E_{f}\epsilon _{f}}$, ${\displaystyle \sigma _{m}=E_{m}\epsilon _{m}}$.^[6]

Other properties

Similar derivations give the rules of mixtures for

• mass density:$${\displaystyle \left({\frac {f}{\rho _{f}}}+{\frac {1-f}{\rho _{c}}}\right)^{-1}\leq \rho _{f}\centerdot f+\rho _{M}\centerdot (1-f)}$$ where f is the atomic percent of fiber in the mixture.
• ultimate tensile strength:$${\displaystyle \left({\frac {f}{\sigma _{UTS,f}}}+{\frac {1-f}{\sigma _{UTS,m}}}\right)^{-1}\leq \sigma _{UTS,c}\leq f\sigma _{UTS,f}+\left(1-f\right)\sigma _{UTS,m}}$$
• thermal conductivity:$${\displaystyle \left({\frac {f}{k_{f}}}+{\frac {1-f}{k_{m}}}\right)^{-1}\leq k_{c}\leq fk_{f}+\left(1-f\right)k_{m}}$$
• electrical conductivity:$${\displaystyle \left({\frac {f}{\sigma _{f}}}+{\frac {1-f}{\sigma _{m}}}\right)^{-1}\leq \sigma _{c}\leq f\sigma _{f}+\left(1-f\right)\sigma _{m}}$$

Generalizations

Some proportion of rule of mixtures and inverse rule of mixtures

A generalized equation for any loading condition between isostrain and isostress can be written as:^[8]

${\displaystyle (E_{c})^{k}=f(E_{f})^{k}+(1-f)(E_{m})^{k}}$

where k is a value between 1 and −1.

More than 2 materials

For a composite containing a mixture of n different materials, each with a material property ${\displaystyle E_{i}}$ and volume fraction ${\displaystyle V_{i}}$, where

${\displaystyle \sum _{i=1}^{n}{V_{i}}=1,}$

then the rule of mixtures can be shown to give:

${\displaystyle E_{c}=\sum _{i=1}^{n}{V_{i}E_{i}}}$

and the inverse rule of mixtures can be shown to give:

${\displaystyle {\frac {1}{E_{c}}}=\sum _{i=1}^{n}{\frac {V_{i}}{E_{i}}}.}$

Finally, generalizing to some combination of the rule of mixtures and inverse rule of mixtures for an n-component system gives:

${\displaystyle (E_{c})^{k}=\sum _{i=1}^{n}V_{i}(E_{i})^{k}}$

See also

When considering the empirical correlation of some physical properties and the chemical composition of compounds, other relationships, rules, or laws, also closely resembles the rule of mixtures:

• Amagat's law – Law of partial volumes of gases
• Gladstone–Dale equation – Optical analysis of liquids, glasses and crystals
• Kopp's law – Heat capacity, with f as the mass fraction
• Richmann's law – Law for the mixing temperature
• Vegard's law – Crystal lattice parameters