Top Qs
Timeline
Chat
Perspective
Runway
Surface used for takeoff or landing From Wikipedia, the free encyclopedia
Remove ads
In aviation, a runway is an elongated, rectangular surface designed for the landing and takeoff of an aircraft.[1] Runways may be a human-made surface (often asphalt, concrete, or a mixture of both) or a natural surface (grass, dirt, gravel, ice, sand or salt). Runways, taxiways and ramps, are sometimes referred to as "tarmac", though very few runways are built using tarmac. Takeoff and landing areas defined on the surface of water for seaplanes are generally referred to as waterways. Runway lengths are now commonly given in meters worldwide, except in North America where feet are commonly used.[2]


Remove ads
History
Summarize
Perspective
In January 1919, aviation pioneer Orville Wright underlined the need for "distinctly marked and carefully prepared landing places, [but] the preparing of the surface of reasonably flat ground [is] an expensive undertaking [and] there would also be a continuous expense for the upkeep."[3]
In 1919, based on WWI experience, the United States Army Air Service published Specifications for Municipal Landing Fields. It specified an 1800 by 1800 foot square with a central 150 foot takeoff runway in the shape of a cross. Through the 1930s though, most army planes landed in any direction, subject to the prevailing winds, on circular groomed and drained turf called "all-over fields." However, tire pressures were limited to less than seventy psi in such fields. After 1935, tire pressures exceeded that limit with increased aircraft size. According to Conway, "Confronted with snow and ice removal in the north, water nearly everywhere, and the demands placed by airlines on regularity, safety, and efficient transshipment of passengers and mail, the technology of the all-over turf field became obsolete in the United States during the 1920s." In 1928, Ford Airfield became the first U.S. airport to have concrete runways, and by 1932, all major U.S. airports had runways..."[4]
Remove ads
Design
Summarize
Perspective
Orientation
The primary consideration in determining runway orientation is the prevailing wind direction, in lieu of spatial constraints or obstructions that may prevent optimal alignment. To mitigate the occurrence of crosswind operations which are more challenging and dangerous, runways at airports are designed to align with the wind's direction. Utilizing runways oriented with the wind direction also allows for aircraft to take-off and land into the headwind, reducing the length of runway used during operations. Taking off and landing into the wind increases the relative air speed of the aircraft to create more lift; this allows aircraft to reach take-off velocity with a shorter amount of ground roll and also allows aircraft to land with a slower ground speed. To determine the prevailing wind directions, analysis of a wind rose is used before constructing airport runways.[5]

Originally in the 1920s and 1930s, airports and air bases (particularly in the United Kingdom) were built in a triangle-like pattern of three runways at 60° angles to each other. The reason was that aviation was only starting, and although it was known that wind affected the runway distance required, not much was known about wind behaviour.[citation needed] As a result, three runways in a triangle-like pattern were built, and the runway with the heaviest traffic would eventually expand into the airport's main runway, while the other two runways would be either abandoned or converted into taxiways.[6]
Naming
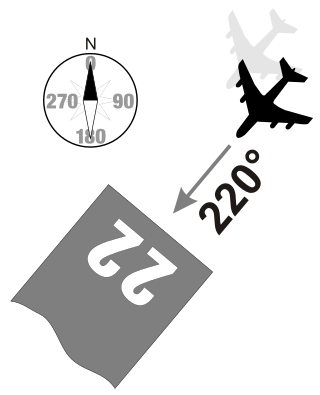

Runways are named by a number between 01 and 36, which is generally the magnetic azimuth of the runway's heading in decadegrees. This heading differs from true north by the local magnetic declination. A runway numbered 09 points east (90°), runway 18 is south (180°), runway 27 points west (270°) and runway 36 points to the north (360° rather than 0°).[7] When taking off from or landing on runway 09, a plane is heading around 90° (east). A runway can normally be used in both directions, and is named for each direction separately: e.g., "runway 15" in one direction is "runway 33" when used in the other. The two numbers differ by 18 (= 180°). For clarity in radio communications, each digit in the runway name is pronounced individually: runway one-five, runway three-three, etc. (instead of "fifteen" or "thirty-three").

A leading zero, for example in "runway zero-six" or "runway zero-one-left", is included for all ICAO and some U.S. military airports (such as Edwards Air Force Base). However, most U.S. civil aviation airports drop the leading zero as required by FAA regulation.[8] This also includes some military airfields such as Cairns Army Airfield. This American anomaly may lead to inconsistencies in conversations between American pilots and controllers in other countries.
Military airbases may include smaller paved runways known as "assault strips" for practice and training next to larger primary runways.[9] These strips eschew the standard numerical naming convention and instead employ the runway's full three digit heading; examples include Dobbins Air Reserve Base's Runway 110/290 and Duke Field's Runway 180/360.[10][11]
Runways with non-hard surfaces, such as small turf airfields and waterways for seaplanes, may use the standard numerical scheme or may use traditional compass point naming, examples include Ketchikan Harbor Seaplane Base's Waterway E/W.[12][13] Airports with unpredictable or chaotic water currents, such as Santa Catalina Island's Pebbly Beach Seaplane Base, may designate their landing area as Waterway ALL/WAY to denote the lack of designated landing direction.[14][13]
Letter suffix

If there is more than one runway pointing in the same direction (parallel runways), each runway is identified by appending left (L), center (C) and right (R) to the end of the runway number to identify its position (when facing its direction)—for example, runways one-five-left (15L), one-five-center (15C), and one-five-right (15R). Runway zero-three-left (03L) becomes runway two-one-right (21R) when used in the opposite direction (derived from adding 18 to the original number for the 180° difference when approaching from the opposite direction). In some countries, regulations mandate that where parallel runways are too close to each other, only one may be used at a time under certain conditions (usually adverse weather).
At large airports with four or more parallel runways (for example, at Chicago O'Hare, Los Angeles, Detroit Metropolitan Wayne County, Hartsfield-Jackson Atlanta, Denver, Dallas–Fort Worth and Orlando), some runway identifiers are shifted by 1 to avoid the ambiguity that would result with more than three parallel runways. For example, in Los Angeles, this system results in runways 6L, 6R, 7L, and 7R, even though all four runways are actually parallel at approximately 69°. At Dallas/Fort Worth International Airport, there are five parallel runways, named 17L, 17C, 17R, 18L, and 18R, all oriented at a heading of 175.4°. Occasionally, an airport with only three parallel runways may use different runway identifiers, such as when a third parallel runway was opened at Phoenix Sky Harbor International Airport in 2000 to the south of existing 8R/26L—rather than confusingly becoming the "new" 8R/26L it was instead designated 7R/25L, with the former 8R/26L becoming 7L/25R and 8L/26R becoming 8/26.
Suffixes may also be used to denote special-use runways. Airports that have seaplane waterways may choose to denote the waterway on charts with the suffix W; such as Daniel K. Inouye International Airport in Honolulu and Lake Hood Seaplane Base in Anchorage.[15] Small airports that host various forms of air traffic may employ additional suffixes to denote special runway types based on the type of aircraft expected to use them, including STOL aircraft (S), gliders (G), rotorcraft (H), and ultralights (U).[13] Runways that are numbered relative to true north rather than magnetic north will use the suffix T; this is advantageous for certain airfields in the far north such as Thule Air Base (08T/26T).[16]
Renumbering
Runway designations may be changed over time as the Earth's magnetic field shifts and their headings shift with it. This is more common at higher latitudes: for example, Fairbanks International Airport in Alaska renames runways roughly every 24 years, most recently in 2009.[17] In northern Canada,[18] runways are designated based on true north, which avoids the need to update them.[19] Nav Canada, Canada's air navigation service provider, has advocated for an industry-wide switch to true north.[20]
As runways are designated with headings rounded to the nearest 10°, some runways are affected sooner than others; e.g. a hypothetical Runway 23 with a heading of 226° would only have to shift to 224° to become Runway 22. Because magnetic drift itself is slow, these changes are uncommon, and not welcomed, as they require accompanying changes in aeronautical charts and descriptive documents. When a runway designation does change, it is often done at night, especially at major airports, because taxiway signs need to be changed and the numbers at each end of the runway need to be repainted to the new runway designators.[citation needed] In 2009 for example, London Stansted Airport in the United Kingdom changed its runway designation from 05/23 to 04/22 during the night.[21]
Remove ads
Declared distances
Summarize
Perspective

Runway dimensions vary from as small as 245 m (804 ft) long and 8 m (26 ft) wide in smaller general aviation airports, to 5,500 m (18,045 ft) long and 80 m (262 ft) wide at large international airports built to accommodate the largest jets, to the huge 11,917 m × 274 m (39,098 ft × 899 ft) lake bed runway 17/35 at Edwards Air Force Base in California – developed as a landing site for the Space Shuttle.[22]
Takeoff and landing distances available are given using one of the following terms:
- Takeoff Run Available (TORA)[23][24] – The length of runway declared available and suitable for the ground run of an airplane taking off.[25]
- Takeoff Distance Available (TODA)[23][24] – The length of the takeoff run available plus the length of the clearway, if clearway is provided.[25] (The clearway length allowed must lie within the aerodrome or airport boundary. According to the Federal Aviation Regulations and Joint Aviation Requirements (JAR) TODA is the lesser of TORA plus clearway or 1.5 times TORA).
- Accelerate-Stop Distance Available (ASDA)[23][24] – The length of the takeoff run available plus the length of the stopway, if stopway is provided.[25]
- Landing Distance Available (LDA)[23][24] – The length of runway that is declared available and suitable for the ground run of an airplane landing.[26]
- Emergency Distance Available (EMDA)[27] – LDA (or TORA) plus a stopway.
Sections
Summarize
Perspective
There are standards for runway markings.[28]
- The runway thresholds are markings across the runway that denote the beginning and end of the designated space for landing and takeoff under non-emergency conditions.[29]
- The runway safety area is the cleared, smoothed and graded area around the paved runway. It is kept free from any obstacles that might impede flight or ground roll of aircraft.
- The runway is the surface from threshold to threshold (including displaced thresholds), which typically features threshold markings, numbers, and centerlines, but excludes blast pads and stopways at both ends.
- Blast pads are often constructed just before the start of a runway where jet blast produced by large planes during the takeoff roll could otherwise erode the ground and eventually damage the runway.
- Stopways, also known as overrun areas, are also constructed at the end of runways as emergency space to stop planes that overrun the runway on landing or a rejected takeoff.
- Blast pads and stopways look similar, and are both marked with yellow chevrons; stopways may optionally be surrounded by red runway lights. The differences are that stopways can support the full weight of an aircraft and are designated for use in an aborted takeoff, while blast pads are often not as strong as the main paved surface of the runway and are not to be used for taxiing, landing, or aborted takeoffs.[30] An engineered materials arrestor system (EMAS) may also be present, which may overlap with the end of the blast pad or stopway and is painted similarly (although an EMAS does not count as part of a stopway).[30]
- Displaced thresholds may be used for taxiing, takeoff, and landing rollout, but not for touchdown. A displaced threshold often exists because of obstacles just before the runway, runway strength, or noise restrictions making the beginning section of runway unsuitable for landings.[31] It is marked with white paint arrows that lead up to the beginning of the landing portion of the runway. As with blast pads, landings on displaced thresholds are not permitted aside from emergency use or exigent circumstance.
- Relocated thresholds are similar to displaced thresholds. They are used to mark a portion of the runway temporarily closed due to construction or runway maintenance. This closed portion of the runway is not available for use by aircraft for takeoff or landing, but it is available for taxi. While methods for identifying the relocated threshold vary, a common way for the relocated threshold to be marked is a ten-foot-wide white bar across the width of the runway.[32]
- Clearway is an area beyond the paved runway, aligned with the runway centerline and under the control of the airport authorities. This area is not less than 500 ft and there are no protruding obstacles except for threshold lights provided they are not higher than 26 inches. There is a limit on the upslope of the clearway of 1.25%. The length of the clearway may be included in the length of the takeoff distance available.[33] For example, if a paved runway is 2,000 metres (6,600 ft) long and there are 400 metres (1,300 ft) of clearway beyond the end of the runway, the takeoff distance available is 2,400 metres (7,900 ft) long. When the runway is to be used for takeoff of a large airplane, the maximum permissible takeoff weight of the airplane can be based on the takeoff distance available, including clearway. Clearway allows large airplanes to take off at a heavier weight than would be allowed if only the length of the paved runway is taken into account.
Remove ads
Markings
Summarize
Perspective
This section needs additional citations for verification. (June 2022) |
There are runway markings and signs on most large runways. Larger runways have a distance remaining sign (black box with white numbers). This sign uses a single number to indicate the remaining distance of the runway in thousands of feet. For example, a 7 will indicate 7,000 ft (2,134 m) remaining. The runway threshold is marked by a line of green lights.

There are three types of runways:
- Visual runways are used at small airstrips and are usually just a strip of grass, gravel, ice, asphalt, or concrete. Although there are usually no markings on a visual runway, they may have threshold markings, designators, and centerlines. Additionally, they do not provide an instrument-based landing procedure; pilots must be able to see the runway to use it. Also, radio communication may not be available and pilots must be self-reliant.
- Non-precision instrument runways are often used at small- to medium-size airports. These runways, depending on the surface, may be marked with threshold markings, designators, centerlines, and sometimes a 1,000 ft (305 m) mark (known as an aiming point, sometimes installed at 1,500 ft (457 m)). While centerlines provide horizontal position guidance, aiming point markers provide vertical position guidance to planes on visual approach.
- Precision instrument runways, which are found at medium- and large-size airports, consist of a blast pad/stopway (optional, for airports handling jets), threshold, designator, centerline, aiming point, and 500 ft (152 m), 1,000 ft (305 m)/1,500 ft (457 m), 2,000 ft (610 m), 2,500 ft (762 m), and 3,000 ft (914 m) touchdown zone marks. Precision runways provide both horizontal and vertical guidance for instrument approaches.
Waterways may be unmarked or marked with buoys that follow maritime notation instead.[34]
For runways and taxiways that are permanently closed, the lighting circuits are disconnected. The runway threshold, runway designation, and touchdown markings are obliterated and yellow "Xs" are placed at each end of the runway and at 1,000 ft (305 m) intervals.[35]
National variants
- In Australia, Canada, the United Kingdom,[36] as well as some other countries or territories (Hong Kong and Macau) all 3-stripe and 2-stripe touchdown zones for precision runways are replaced with one-stripe touchdown zones.
- In some South American countries like Colombia, Ecuador and Peru, one 3-stripe is added and a 2-stripe is replaced with the aiming point.
- Some European countries replace the aiming point with a 3-stripe touchdown zone.
- Runways in Norway have yellow markings instead of the usual white ones. This also occurs in some airports in Japan, Sweden, and Finland. The yellow markings are used to ensure better contrast against snow.
- Runways may have different types of equipment on each end. To reduce costs, many airports do not install precision guidance equipment on both ends. Runways with one precision end and any other type of end can install the full set of touchdown zones, even if some are past the midpoint. Runways with precision markings on both ends omit touchdown zones within 900 ft (274 m) of the midpoint, to avoid ambiguity over the end with which the zone is associated.
Remove ads
Lighting
Summarize
Perspective


A line of lights on an airfield or elsewhere to guide aircraft in taking off or coming in to land or an illuminated runway is sometimes also known as a flare path.
Technical specifications


Runway lighting is used at airports during periods of darkness and low visibility. Seen from the air, runway lights form an outline of the runway. A runway may have some or all of the following:[37]
- Runway end identifier lights (REIL) – unidirectional (facing approach direction) or omnidirectional pair of synchronized flashing lights installed at the runway threshold, one on each side.
- Runway end lights – a pair of four lights on each side of the runway on precision instrument runways, these lights extend along the full width of the runway. These lights show green when viewed by approaching aircraft and red when seen from the runway.
- Runway edge lights – white elevated lights that run the length of the runway on either side. On precision instrument runways, the edge-lighting becomes amber in the last 2,000 ft (610 m) of the runway, or last third of the runway, whichever is less. Taxiways are differentiated by being bordered by blue lights, or by having green center lights, depending on the width of the taxiway, and the complexity of the taxi pattern.
- Runway centerline lighting system (RCLS) – lights embedded into the surface of the runway at 50 ft (15 m) intervals along the runway centerline on some precision instrument runways. White except the last 900 m (3,000 ft): alternate white and red for next 600 m (1,969 ft) and red for last 300 m (984 ft).[37]
- Touchdown zone lights (TDZL[23]) – rows of white light bars (with three in each row) at 30 or 60 m (98 or 197 ft) intervals on either side of the centerline for 900 m (3,000 ft).[37]
- Taxiway centerline lead-off lights – installed along lead-off markings, alternate green and yellow lights embedded into the runway pavement. It starts with green light at about the runway centerline to the position of first centerline light beyond the Hold-Short markings on the taxiway.
- Taxiway centerline lead-on lights – installed the same way as taxiway centerline lead-off Lights, but directing airplane traffic in the opposite direction.
- Land and hold short lights – a row of white pulsating lights installed across the runway to indicate hold short position on some runways that are facilitating land and hold short operations (LAHSO).[37]
- Approach lighting system (ALS) – a lighting system installed on the approach end of an airport runway and consists of a series of lightbars, strobe lights, or a combination of the two that extends outward from the runway end.
According to Transport Canada's regulations,[38] the runway-edge lighting must be visible for at least 2 mi (3 km). Additionally, a new system of advisory lighting, runway status lights, is currently being tested in the United States.[39]
The edge lights must be arranged such that:
- the minimum distance between lines is 75 ft (23 m), and maximum is 200 ft (61 m)
- the maximum distance between lights within each line is 200 ft (61 m)
- the minimum length of parallel lines is 1,400 ft (427 m)
- the minimum number of lights in the line is 8.[40]

Control of lighting system
Typically the lights are controlled by a control tower, a flight service station or another designated authority. Some airports/airfields (particularly uncontrolled ones) are equipped with pilot-controlled lighting, so that pilots can temporarily turn on the lights when the relevant authority is not available.[41] This avoids the need for automatic systems or staff to turn the lights on at night or in other low visibility situations. This also avoids the cost of having the lighting system on for extended periods. Smaller airports may not have lighted runways or runway markings. Particularly at private airfields for light planes, there may be nothing more than a windsock beside a landing strip.
Remove ads
Safety
Types of runway safety incidents include:
- Runway excursion – an incident involving only a single aircraft, where it makes an inappropriate exit from the runway (e.g. Thai Airways Flight 679).
- Runway overrun (also known as an overshoot) – a type of excursion where the aircraft is unable to stop before the end of the runway (e.g. Air France Flight 358, TAM Airlines Flight 3054, Air India Express Flight 812).
- Runway incursion – an incident involving incorrect presence of a vehicle, person or another aircraft on the runway (e.g. Aeroflot Flight 3352, Scandinavian Airlines Flight 686).
- Runway confusion – an aircraft makes use of the wrong runway for landing or takeoff (e.g. Singapore Airlines Flight 006, Western Airlines Flight 2605).
- Runway undershoot – an aircraft that lands short of the runway (e.g. British Airways Flight 38, Asiana Airlines Flight 214).
Remove ads
Surface
Summarize
Perspective
This section has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|

The choice of material used to construct the runway depends on the use and the local ground conditions. For a major airport, where the ground conditions permit, the most satisfactory type of pavement for long-term minimum maintenance is concrete. Although certain airports have used reinforcement in concrete pavements, this is generally found to be unnecessary, with the exception of expansion joints across the runway where a dowel assembly, which permits relative movement of the concrete slabs, is placed in the concrete. Where it can be anticipated that major settlements of the runway will occur over the years because of unstable ground conditions, it is preferable to install asphalt concrete surface, as it is easier to patch on a periodic basis. Fields with very low traffic of light planes may use a sod surface. Some runways make use of salt flats.
For pavement designs, borings are taken to determine the subgrade condition, and based on the relative bearing capacity of the subgrade, the specifications are established. For heavy-duty commercial aircraft, the pavement thickness, no matter what the top surface, varies from 10 to 48 in (25 to 122 cm), including subgrade.
Airport pavements have been designed by two methods. The first, Westergaard, is based on the assumption that the pavement is an elastic plate supported on a heavy fluid base with a uniform reaction coefficient known as the K value. Experience has shown that the K values on which the formula was developed are not applicable for newer aircraft with very large footprint pressures.
The second method is called the California bearing ratio and was developed in the late 1940s. It is an extrapolation of the original test results, which are not applicable to modern aircraft pavements or to modern aircraft landing gear. Some designs were made by a mixture of these two design theories. A more recent method is an analytical system based on the introduction of vehicle response as an important design parameter. Essentially it takes into account all factors, including the traffic conditions, service life, materials used in the construction, and, especially important, the dynamic response of the vehicles using the landing area.
Because airport pavement construction is so expensive, manufacturers aim to minimize aircraft stresses on the pavement. Manufacturers of the larger planes design landing gear so that the weight of the plane is supported on larger and more numerous tires. Attention is also paid to the characteristics of the landing gear itself, so that adverse effects on the pavement are minimized. Sometimes it is possible to reinforce a pavement for higher loading by applying an overlay of asphaltic concrete or portland cement concrete that is bonded to the original slab. Post-tensioning concrete has been developed for the runway surface. This permits the use of thinner pavements and should result in longer concrete pavement life. Because of the susceptibility of thinner pavements to frost heave, this process is generally applicable only where there is no appreciable frost action.
Pavement surface

Runway pavement surface is prepared and maintained to maximize friction for wheel braking. To minimize hydroplaning following heavy rain, the pavement surface is usually grooved so that the surface water film flows into the grooves and the peaks between grooves will still be in contact with the aircraft tyres. To maintain the macrotexturing built into the runway by the grooves, maintenance crews engage in airfield rubber removal or hydrocleaning in order to meet required FAA, or other aviation authority friction levels.

Pavement subsurface drainage and underdrains
Subsurface underdrains help provide extended life and excellent and reliable pavement performance. At the Hartsfield Atlanta, GA airport the underdrains usually consist of trenches 18 in (46 cm) wide and 48 in (120 cm) deep from the top of the pavement. A perforated plastic tube (5.9 in (15 cm) in diameter) is placed at the bottom of the ditch. The ditches are filled with gravel size crushed stone.[42] Excessive moisture under a concrete pavement can cause pumping, cracking, and joint failure.[43]
Surface type codes

In aviation charts, the surface type is usually abbreviated to a three-letter code.
The most common hard surface types are asphalt and concrete. The most common soft surface types are grass and gravel.
Remove ads
Length
Summarize
Perspective
This section needs additional citations for verification. (June 2022) |
A runway of at least 1,800 m (5,900 ft) in length is usually adequate for aircraft weights below approximately 100,000 kg (220,000 lb). Larger aircraft including widebodies will usually require at least 2,400 m (7,900 ft) at sea level. International widebody flights, which carry substantial amounts of fuel and are therefore heavier, may also have landing requirements of 3,200 m (10,500 ft) or more and takeoff requirements of 4,000 m (13,000 ft). The Boeing 747 is considered to have the longest takeoff distance of the more common aircraft types and has set the standard for runway lengths of larger international airports.[44]
At sea level, 3,200 m (10,500 ft) can be considered an adequate length to land virtually any aircraft. For example, at O'Hare International Airport, when landing simultaneously on 4L/22R and 10/28 or parallel 9R/27L, it is routine for arrivals from East Asia, which would normally be vectored for 4L/22R (2,300 m (7,546 ft)) or 9R/27L (2,400 m (7,874 ft)) to request 28R (4,000 m (13,123 ft)). It is always accommodated, although occasionally with a delay. Another example is that the Luleå Airport in Sweden was extended to 3,500 m (11,483 ft) to allow any fully loaded freight aircraft to take off. These distances are also influenced by the runway grade (slope) such that, for example, each 1 percent of runway down slope increases the landing distance by 10 percent.[45]
An aircraft taking off at a higher altitude must do so at reduced weight due to decreased density of air at higher altitudes, which reduces engine power and wing lift. An aircraft must also take off at a reduced weight in hotter or more humid conditions (see density altitude). In the worst case, this is colloquially referred to as hot and high operation, among the most challenging conditions for takeoff performance. Most commercial aircraft carry manufacturer's tables showing the adjustments required for a given temperature.
- In the 1980s, Leeds Bradford International Airport extended its runway to take wide-body aircraft by building an overpass over the A658 road.
- Road crossing of (Shetland) A970 with Sumburgh Airport's runway. The movable barrier closes when aircraft land or take off.
- Gibraltar International Airport's runway 09/27, used to be crossed by the one road between Gibraltar and Spain.
- A parachute may be used to slow down craft, in this case the Space Shuttle Atlantis.
Remove ads
See also
- Engineered materials arrestor system
- Helipad
- Highway strip
- ICAO recommendations on use of the International System of Units
- Instrument landing system (ILS)
- List of airports
- Pavement classification number (PCN)
- Precision approach path indicator
- Roll way, sometimes referred as a runway[46]
- Runway visual range
- Tabletop runway
- Visual approach slope indicator
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads







