Semiperfect number

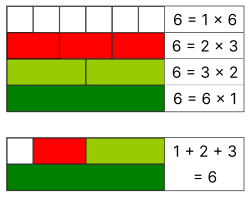
In number theory, a semiperfect number or pseudoperfect number is a natural number n that is equal to the sum of all or some of its proper divisors. A semiperfect number that is equal to the sum of all its proper divisors is a perfect number.

Semiperfect number

Demonstration, with Cuisenaire rods, of the perfection of the number 6.
Total no. of terms	infinity
First terms	6, 12, 18, 20, 24, 28, 30
OEIS index	A005835 Pseudoperfect (or semiperfect) numbers

The first few semiperfect numbers are: 6, 12, 18, 20, 24, 28, 30, 36, 40, ... (sequence A005835 in the OEIS)

Properties

• Every multiple of a semiperfect number is semiperfect.^[1] A semiperfect number that is not divisible by any smaller semiperfect number is called primitive.
• Every number of the form 2^mp for a natural number m and an odd prime number p such that p < 2^m+1 is also semiperfect.
  • In particular, every number of the form 2^m(2^m+1 − 1) is semiperfect, and indeed perfect if 2^m+1 − 1 is a Mersenne prime.
• The smallest odd semiperfect number is 945 (see, e.g., Friedman 1993).
• A semiperfect number is necessarily either perfect or abundant. An abundant number that is not semiperfect is called a weird number.
• With the exception of 2, all primary pseudoperfect numbers are semiperfect.
• Every practical number that is not a power of two is semiperfect.
• The natural density of the set of semiperfect numbers exists.^[2]

Primitive semiperfect numbers

A primitive semiperfect number (also called a primitive pseudoperfect number, irreducible semiperfect number or irreducible pseudoperfect number) is a semiperfect number that has no semiperfect proper divisor.^[2]

The first few primitive semiperfect numbers are 6, 20, 28, 88, 104, 272, 304, 350, ... (sequence A006036 in the OEIS)

There are infinitely many such numbers. All numbers of the form 2^mp, with p a prime between 2^m and 2^m+1, are primitive semiperfect, but this is not the only form: for example, 770.^[1][2] There are infinitely many odd primitive semiperfect numbers, the smallest being 945, a result of Paul Erdős:^[2] there are also infinitely many primitive semiperfect numbers that are not harmonic divisor numbers.^[1]

Every semiperfect number is a multiple of a primitive semiperfect number.

See also

• Hemiperfect number
• Erdős–Nicolas number