Small-gain theorem

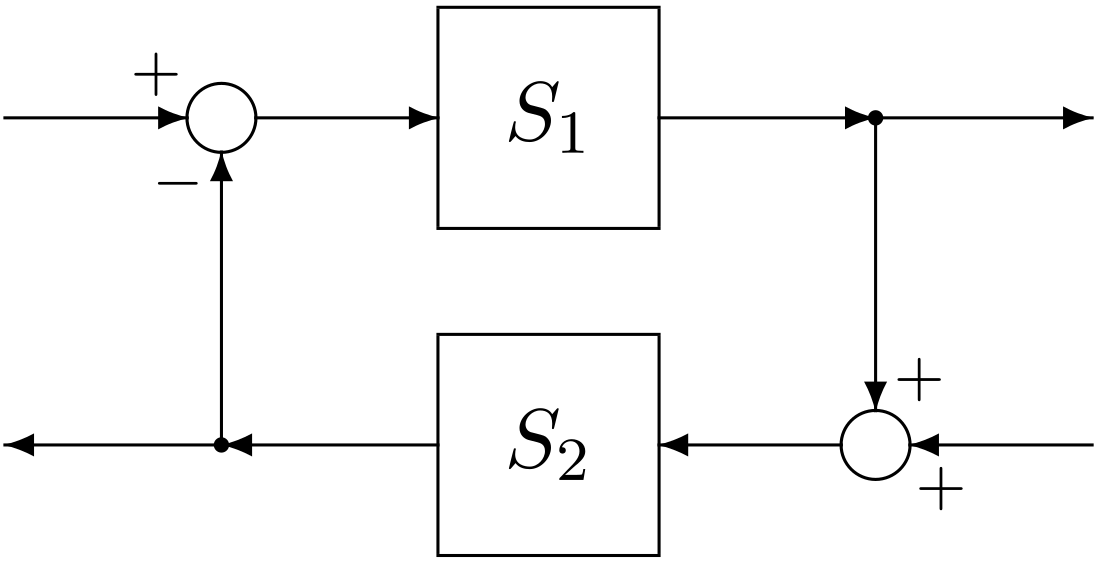
In nonlinear systems, the formalism of input-output stability is an important tool in studying the stability of interconnected systems since the gain of a system directly relates to how the norm of a signal increases or decreases as it passes through the system. The small-gain theorem gives a sufficient condition for finite-gain ${\displaystyle {\mathcal {L}}}$ stability of the feedback connection. The small gain theorem was proved by George Zames in 1966. It can be seen as a generalization of the Nyquist criterion to non-linear time-varying MIMO systems (systems with multiple inputs and multiple outputs).

Feedback connection between systems S₁ and S₂.

Theorem. Assume two stable systems ${\displaystyle S_{1}}$ and ${\displaystyle S_{2}}$ are connected in a feedback loop, then the closed loop system is input-output stable if ${\displaystyle \|S_{1}\|\cdot \|S_{2}\|<1}$ and both ${\displaystyle S_{1}}$ and ${\displaystyle S_{2}}$ are stable by themselves. (This norm is typically the ${\displaystyle {\mathcal {H}}_{\infty }}$-norm, the size of the largest singular value of the transfer function over all frequencies. Any induced Norm will also lead to the same results).^[1][2][3]

A complementing result due to Georgiou, Khammash and Megretski (1997), referred to as the large-gain theorem, quantifies the minimum loop-gain needed to stabilize an unstable, possibly nonlinear and time-varying, plant; the minimum loop-gain being 1.^[4]