Small snub icosicosidodecahedron

In geometry, the small snub icosicosidodecahedron or snub disicosidodecahedron is a uniform star polyhedron, indexed as U₃₂. It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. Its stellation core is a truncated pentakis dodecahedron. It also called a holosnub icosahedron, ß{3,5}.

Small snub icosicosidodecahedron
Type	Uniform star polyhedron
Elements	F = 112, E = 180 V = 60 (χ = −8)
Faces by sides	(40+60){3}+12{5/2}
Coxeter diagram
Wythoff symbol	| 5/2 3 3
Symmetry group	Ih, [5,3], *532
Index references	U32, C41, W110
Dual polyhedron	Small hexagonal hexecontahedron
Vertex figure	35.5/2
Bowers acronym	Seside

3D model of a small snub icosicosidodecahedron

The 40 non-snub triangular faces form 20 coplanar pairs, forming star hexagons that are not quite regular. Unlike most snub polyhedra, it has reflection symmetries.

Convex hull

Its convex hull is a nonuniform truncated icosahedron.

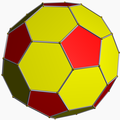Truncated icosahedron (regular faces)

Convex hull (isogonal hexagons)

Small snub icosicosidodecahedron

Cartesian coordinates

Let ${\displaystyle \xi =-{\frac {3}{2}}+{\frac {1}{2}}{\sqrt {1+4\phi }}\approx -0.1332396008261379}$ be largest (least negative) zero of the polynomial ${\displaystyle P=x^{2}+3x+\phi ^{-2}}$, where ${\displaystyle \phi }$ is the golden ratio. Let the point ${\displaystyle p}$ be given by

${\displaystyle p={\begin{pmatrix}\phi ^{-1}\xi +\phi ^{-3}\\\xi \\\phi ^{-2}\xi +\phi ^{-2}\end{pmatrix}}}$.

Let the matrix ${\displaystyle M}$ be given by

${\displaystyle M={\begin{pmatrix}1/2&-\phi /2&1/(2\phi )\\\phi /2&1/(2\phi )&-1/2\\1/(2\phi )&1/2&\phi /2\end{pmatrix}}}$.

${\displaystyle M}$ is the rotation around the axis ${\displaystyle (1,0,\phi )}$ by an angle of ${\displaystyle 2\pi /5}$, counterclockwise. Let the linear transformations ${\displaystyle T_{0},\ldots ,T_{11}}$ be the transformations which send a point ${\displaystyle (x,y,z)}$ to the even permutations of ${\displaystyle (\pm x,\pm y,\pm z)}$ with an even number of minus signs. The transformations ${\displaystyle T_{i}}$ constitute the group of rotational symmetries of a regular tetrahedron. The transformations ${\displaystyle T_{i}M^{j}}$ ${\displaystyle (i=0,\ldots ,11}$, ${\displaystyle j=0,\ldots ,4)}$ constitute the group of rotational symmetries of a regular icosahedron. Then the 60 points ${\displaystyle T_{i}M^{j}p}$ are the vertices of a small snub icosicosidodecahedron. The edge length equals ${\displaystyle -2\xi }$, the circumradius equals ${\displaystyle {\sqrt {-4\xi -\phi ^{-2}}}}$, and the midradius equals ${\displaystyle {\sqrt {-\xi }}}$.

For a small snub icosicosidodecahedron whose edge length is 1, the circumradius is

${\displaystyle R={\frac {1}{2}}{\sqrt {\frac {\xi -1}{\xi }}}\approx 1.4581903307387025}$

Its midradius is

${\displaystyle r={\frac {1}{2}}{\sqrt {\frac {-1}{\xi }}}\approx 1.369787954633799}$

The other zero of ${\displaystyle P}$ plays a similar role in the description of the small retrosnub icosicosidodecahedron.

See also

• List of uniform polyhedra
• Small retrosnub icosicosidodecahedron

External links

• Weisstein, Eric W. "Small snub icosicosidodecahedron". MathWorld.
• Klitzing, Richard. "3D star small snub icosicosidodecahedron".