Icosahedron

In geometry, an icosahedron (/ˌaɪkɒsəˈhiːdrən, -kə-, -koʊ-/ or /aɪˌkɒsəˈhiːdrən/^[1]) is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty' and ἕδρα (hédra) 'seat'. The plural can be either "icosahedra" (/-drə/) or "icosahedrons".

There are infinitely many non-similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the (convex, non-stellated) regular icosahedron—one of the Platonic solids—whose faces are 20 equilateral triangles.

Regular icosahedra

Main articles: Regular icosahedron and Great icosahedron

Two kinds of regular icosahedra: the convex and non-convex

There are two objects, one convex and one nonconvex, that can both be referred to as regular icosahedra, characterized by 30 edges and 20 triangular faces. The term "regular icosahedron" generally refers to a convex polyhedron, both a deltahedron and a Platonic solid; it is also called "icosahedron" for a plain term.^[2] A non-convex polyhedron version is the great icosahedron, a Kepler–Poinsot polyhedron. Both have icosahedral symmetry.

There are 59 stellations of a regular icosahedron according to Coxeter et al. in The Fifty-Nine Icosahedra. Being stellated means that a polyhedron extends its faces or edges until they meet to form a new polyhedron. It is done symmetrically so that the resulting figure retains the overall symmetry of the parent figure. The regular icosahedron and the great icosahedron are among them. Other stellations have more than one face in each plane or form compounds of simpler polyhedra. These are not strictly icosahedra, although they are often referred to as such.^[3]

Notable stellations of the icosahedron
Regular	Regular star	Uniform duals
(Convex) icosahedron	Great icosahedron	Small triambic icosahedron	Medial triambic icosahedron	Great triambic icosahedron
Regular compounds			Others
Compound of five octahedra	Compound of five tetrahedra	Compound of ten tetrahedra	Excavated dodecahedron	Final stellation

Pyritohedral icosahedra

Construction from the vertices of a truncated octahedron, showing internal rectangles.

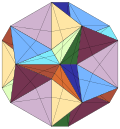
A regular icosahedron can be distorted or marked up as a lower pyritohedral symmetry,^[4][5] and is called a snub octahedron, snub tetratetrahedron, snub tetrahedron, and pseudo-icosahedron.^[6] This can be seen as an alternated truncated octahedron. If all the triangles are equilateral, the symmetry can also be distinguished by colouring the 8 and 12 triangle sets differently.Pyritohedral symmetry has the symbol (3*2), [3⁺,4], with order 24. Tetrahedral symmetry has the symbol (332), [3,3]⁺, with order 12. These lower symmetries allow geometric distortions from 20 equilateral triangular faces, instead having 8 equilateral triangles and 12 congruent isosceles triangles. These symmetries offer Coxeter diagrams: and respectively, each representing the lower symmetry to the regular icosahedron , (*532), [5,3] icosahedral symmetry of order 120.

The Cartesian coordinates of the 12 vertices can be defined by the vectors defined by all the possible cyclic permutations and sign-flips of coordinates of the form (2, 1, 0). These coordinates represent the truncated octahedron with alternated vertices deleted. This construction is called a snub tetrahedron in its regular icosahedron form, generated by the same operations carried out starting with the vector (ϕ, 1, 0), where ϕ is the golden ratio.^[5]

Progressions between an octahedron, pseudoicosahedron, and cuboctahedron. The cuboctahedron can flex this way even if its edges (but not its faces) are rigid.

A regular icosahedron is topologically identical to a cuboctahedron with its 6 square faces bisected on diagonals with pyritohedral symmetry. The icosahedra with pyritohedral symmetry constitute an infinite family of polyhedra which include the cuboctahedron, regular icosahedron, Jessen's icosahedron, and double cover octahedron. Cyclical kinematic transformations occur among the members of this family.

Other icosahedra

Other icosahedra, which include convex and non-convex, are the following, alongside their descriptions:

• 
  Jessen's icosahedron sometimes called "Jessen's orthogonal icosahedron": a polyhedron with eight equilateral triangles and twelve isosceles faces icosahedron as its faces. Arranged differently, the figure is non-convex and has right dihedral angles.
• 
  Rhombic icosahedron: a zonohedron made up of 20 congruent rhombs. It can be derived from the rhombic triacontahedron by removing 10 middle faces. Even though all the faces are congruent, the rhombic icosahedron is not face-transitive.
• 
  A pyramid with 19 triangular faces and 1 dodecagonal base.
• 
  A prism with 18 lateral faces and 2 dodecagonal bases.
• 
  An antiprism with a nine-sided polygonal base.
• 
  A bipyramid with twenty-sided triangular faces.
• 
  Gyroelongated triangular cupola: A Johnson solid with 16 triangles, 3 pentagon, and 1 hexagon.
• 
  An elongated triangular orthobicupola is a Johnson solid with 8 triangles and 12 squares. A similar Johnson solid with the same number and kinds of faces is an elongated triangular gyrobicupola, but its construction is shown differently by rotating one of its triangular cupola.
• 
  A parabiaugmented dodecahedron is a Johnson solid with 10 triangles and 10 pentagons. The number and kinds of faces is the same as a metabiaugmented dodecahedron. The difference between these two is the construction, attaching a pentagonal pyramid to the face of a regular dodecahedron differently.
• 
  Triangular hebesphenorotunda: the last Johnson solid with 13 equilateral triangles, 3 squares, 3 pentagons, and 1 hexagon.

See also

• Truncated icosahedron
• 600-cell
• Icosoku
• Icosahedral twins - Nanoparticles which are often close to perfect icosahedra.