Top Qs
Timeline
Chat
Perspective
Steric 6-cubes
From Wikipedia, the free encyclopedia
Remove ads
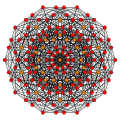
In six-dimensional geometry, a steric 6-cube is a convex uniform 6-polytope. There are unique 4 steric forms of the 6-cube.
Steric 6-cube
| Steric 6-cube | |
|---|---|
| Type | uniform 6-polytope |
| Schläfli symbol | t0,3{3,33,1} h4{4,34} |
| Coxeter-Dynkin diagram | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 3360 |
| Vertices | 480 |
| Vertex figure | |
| Coxeter groups | D6, [33,1,1] |
| Properties | convex |
Alternate names
- Runcinated demihexeract
- Runcinated 6-demicube
- Small prismated hemihexeract (Acronym: sophax) (Jonathan Bowers)[1]
Cartesian coordinates
The Cartesian coordinates for the 480 vertices of a steric 6-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±1,±1,±3)
with an odd number of plus signs.
Images
Related polytopes
Remove ads
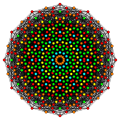
Stericantic 6-cube
Alternate names
- Runcitruncated demihexeract
- Runcitruncated 6-demicube
- Prismatotruncated hemihexeract (Acronym: pithax) (Jonathan Bowers)[2]
Cartesian coordinates
The Cartesian coordinates for the 2880 vertices of a stericantic 6-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±3,±3,±5)
with an odd number of plus signs.
Images
Remove ads
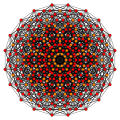
Steriruncic 6-cube
Alternate names
- Runcicantellated demihexeract
- Runcicantellated 6-demicube
- Prismatorhombated hemihexeract (Acronym: prohax) (Jonathan Bowers)[3]
Cartesian coordinates
The Cartesian coordinates for the 1920 vertices of a steriruncic 6-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±1,±3,±5)
with an odd number of plus signs.
Images
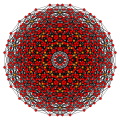
Steriruncicantic 6-cube
Alternate names
- Runcicantitruncated demihexeract
- Runcicantitruncated 6-demicube
- Great prismated hemihexeract (Acronym: gophax) (Jonathan Bowers)[4]
Cartesian coordinates
The Cartesian coordinates for the 5760 vertices of a steriruncicantic 6-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±3,±5,±7)
with an odd number of plus signs.
Images
Remove ads
Related polytopes
There are 47 uniform polytopes with D6 symmetry, 31 are shared by the B6 symmetry, and 16 are unique:
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads