Symmetric relation

A symmetric relation is a type of binary relation. Formally, a binary relation R over a set X is symmetric if:^[1]

${\displaystyle \forall a,b\in X(aRb\Leftrightarrow bRa),}$

Transitive binary relations v t e
Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Total, Semiconnex Anti- reflexive Equivalence relation Y ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Preorder (Quasiorder) ✗ ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Partial order ✗ Y ✗ ✗ ✗ ✗ Y ✗ ✗ Total preorder ✗ ✗ Y ✗ ✗ ✗ Y ✗ ✗ Total order ✗ Y Y ✗ ✗ ✗ Y ✗ ✗ Prewellordering ✗ ✗ Y Y ✗ ✗ Y ✗ ✗ Well-quasi-ordering ✗ ✗ ✗ Y ✗ ✗ Y ✗ ✗ Well-ordering ✗ Y Y Y ✗ ✗ Y ✗ ✗ Lattice ✗ Y ✗ ✗ Y Y Y ✗ ✗ Join-semilattice ✗ Y ✗ ✗ Y ✗ Y ✗ ✗ Meet-semilattice ✗ Y ✗ ✗ ✗ Y Y ✗ ✗ Strict partial order ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Strict weak order ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Strict total order ✗ Y Y ✗ ✗ ✗ ✗ Y Y Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Definitions, for all ${\displaystyle a,b}$ and ${\displaystyle S\neq \varnothing$ :} ${\displaystyle {\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}aRb{\text{ and }}&bRa\\\Rightarrow a={}&b\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ or }}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}\min S\\{\text{exists}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\vee b\\{\text{exists}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\wedge b\\{\text{exists}}\end{aligned}}}$ ${\displaystyle aRa}$ ${\displaystyle {\text{not }}aRa}$ ${\displaystyle {\begin{aligned}aRb\Rightarrow \\{\text{not }}bRa\end{aligned}}}$
Y indicates that the column's property is always true for the row's term (at the very left), while ✗ indicates that the property is not guaranteed in general (it might, or might not, hold). For example, that every equivalence relation is symmetric, but not necessarily antisymmetric, is indicated by Y in the "Symmetric" column and ✗ in the "Antisymmetric" column, respectively. All definitions tacitly require the homogeneous relation ${\displaystyle R}$ be transitive: for all ${\displaystyle a,b,c,}$ if ${\displaystyle aRb}$ and ${\displaystyle bRc}$ then ${\displaystyle aRc.}$ A term's definition may require additional properties that are not listed in this table.

where the notation aRb means that (a, b) ∈ R.

An example is the relation "is equal to", because if a = b is true then b = a is also true. If R^T represents the converse of R, then R is symmetric if and only if R = R^T.^[2]

Symmetry, along with reflexivity and transitivity, are the three defining properties of an equivalence relation.^[1]

Examples

In mathematics

• "is equal to" (equality) (whereas "is less than" is not symmetric)
• "is comparable to", for elements of a partially ordered set
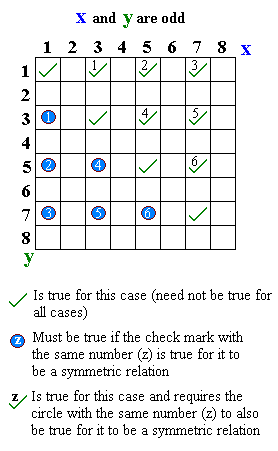
• "... and ... are odd":

Outside mathematics

• "is married to" (in most legal systems)
• "is a fully biological sibling of"
• "is a homophone of"
• "is a co-worker of"
• "is a teammate of"

Relationship to asymmetric and antisymmetric relations

Symmetric and antisymmetric relations

By definition, a nonempty relation cannot be both symmetric and asymmetric (where if a is related to b, then b cannot be related to a (in the same way)). However, a relation can be neither symmetric nor asymmetric, which is the case for "is less than or equal to" and "preys on").

Symmetric and antisymmetric (where the only way a can be related to b and b be related to a is if a = b) are actually independent of each other, as these examples show.

Mathematical examples

	Symmetric	Not symmetric
Antisymmetric	equality	divides, less than or equal to
Not antisymmetric	congruence in modular arithmetic	// (integer division), most nontrivial permutations

Non-mathematical examples

	Symmetric	Not symmetric
Antisymmetric	is the same person as, and is married	is the plural of
Not antisymmetric	is a full biological sibling of	preys on

Properties

• A symmetric and transitive relation is always quasireflexive.^[a]
• One way to count the symmetric relations on n elements, that in their binary matrix representation the upper right triangle determines the relation fully, and it can be arbitrary given, thus there are as many symmetric relations as n × n binary upper triangle matrices, 2^n(n+1)/2.^[3]

Number of n-element binary relations of different types

Elem­ents	Any	Transitive	Reflexive	Symmetric	Preorder	Partial order	Total preorder	Total order	Equivalence relation
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3,994	4,096	1,024	355	219	75	24	15
n	2n2		2n(n−1)	2n(n+1)/2			∑n k=0 k!S(n, k)	n!	∑n k=0 S(n, k)
OEIS	A002416	A006905	A053763	A006125	A000798	A001035	A000670	A000142	A000110

Note that S(n, k) refers to Stirling numbers of the second kind.

Notes

1. If xRy, the yRx by symmetry, hence xRx by transitivity. The proof of xRy ⇒ yRy is similar.

References

1. Biggs, Norman L. (2002). Discrete Mathematics. Oxford University Press. p. 57. ISBN 978-0-19-871369-2.
2. "MAD3105 1.2". Florida State University Department of Mathematics. Florida State University. Retrieved 30 March 2024.
3. Sloane, N. J. A. (ed.). "Sequence A006125". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.

See also

• Commutative property – Property of some mathematical operations
• Symmetry in mathematics
• Symmetry – Mathematical invariance under transformations