Tamari lattice

In mathematics, the Tamari lattice of order n, introduced by Dov Tamari (1962) and sometimes notated T_n or Y_n, is a partially ordered set in which the elements consist of all ways of bracketing a sequence of n+1 letters using n pairs of parentheses, with the ordering induced by only rightward applications of the associative law ((xy)z) → (x(yz)). For instance, T₃ contains five elements (((ab)c)d), ((ab)(cd)), ((a(bc))d), (a((bc)d)), and (a(b(cd))), with (((ab)c)d) < ((ab)(cd)) < (a(b(cd))) and (((ab)c)d) < ((a(bc))d) < (a((bc)d)) < (a(b(cd))). (The outermost pair of parentheses is redundant and often omitted when naming the elements of T_n, as in the depiction of T₄ shown in the figure.)

Tamari lattice of order 4

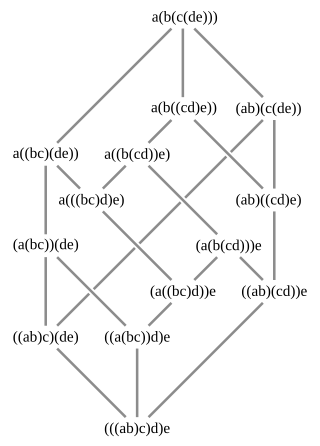
The number of elements in the Tamari lattice of order n is the nth Catalan number C_n. Its Hasse diagram is isomorphic to the skeleton of the associahedron of dimension n-1.

The lattice property for the order (i.e., that any two bracketings have a join and meet) is non-trivial and was first established rigorously by (Friedman & Tamari 1967), with another simpler proof later given by (Huang & Tamari 1972).

The Tamari lattice can be described in several other equivalent ways:

• It is the poset of binary trees with n nodes and n+1 leaves, ordered by tree rotation operations.
• It is the poset of triangulations of a convex n-gon, ordered by flip operations that substitute one diagonal of the polygon for another.
• It is the poset of sequences of n integers a₁, ..., a_n, ordered coordinatewise, such that i ≤ a_i ≤ n and if i ≤ j ≤ a_i then a_j ≤ a_i (Huang & Tamari 1972).
• It is the poset of ordered forests, in which one forest is earlier than another in the partial order if, for every j, the jth node in a preorder traversal of the first forest has at least as many descendants as the jth node in a preorder traversal of the second forest (Knuth 2005).

Notation and indexing

The notation Y_n is sometimes used for the Tamari lattice of order n (Chapoton 2005), which has the mnemonic value that the elements of the lattice may be considered as binary trees with n Y-shaped binary nodes. Note that the corresponding associahedron of dimension n-1 is notated K_n+1 since the indexing is by the number of leaves in the binary trees that form its vertices, rather than by the number of nodes.

References

• Chapoton, F. (2005), "Sur le nombre d'intervalles dans les treillis de Tamari", Séminaire Lotharingien de Combinatoire (in French), 55 (55): 2368, arXiv:math/0602368, Bibcode:2006math......2368C, MR 2264942.
• Csar, Sebastian A.; Sengupta, Rik; Suksompong, Warut (2014), "On a Subposet of the Tamari Lattice", Order, 31 (3): 337–363, arXiv:1108.5690, doi:10.1007/s11083-013-9305-5, MR 3265974.
• Early, Edward (2004), "Chain lengths in the Tamari lattice", Annals of Combinatorics, 8 (1): 37–43, doi:10.1007/s00026-004-0203-9, MR 2061375.
• Friedman, Haya; Tamari, Dov (1967), "Problèmes d'associativité: Une structure de treillis finis induite par une loi demi-associative", Journal of Combinatorial Theory (in French), 2 (3): 215–242, doi:10.1016/S0021-9800(67)80024-3, MR 0238984.
• Geyer, Winfried (1994), "On Tamari lattices", Discrete Mathematics, 133 (1–3): 99–122, doi:10.1016/0012-365X(94)90019-1, MR 1298967.
• Huang, Samuel; Tamari, Dov (1972), "Problems of associativity: A simple proof for the lattice property of systems ordered by a semi-associative law", Journal of Combinatorial Theory, Series A, 13: 7–13, doi:10.1016/0097-3165(72)90003-9, MR 0306064.
• Knuth, Donald E. (2005), "Draft of Section 7.2.1.6: Generating All Trees", The Art of Computer Programming, vol. IV, p. 34.
• Tamari, Dov (1962), "The algebra of bracketings and their enumeration", Nieuw Archief voor Wiskunde, Series 3, 10: 131–146, MR 0146227.