Thue number

In the mathematical area of graph theory, the Thue number of a graph is a variation of the chromatic index, defined by Alon et al. (2002) and named after mathematician Axel Thue, who studied the squarefree words used to define this number.

The Thue number of the 5-cycle is four.

Alon et al. define a nonrepetitive coloring of a graph to be an assignment of colors to the edges of the graph, such that there does not exist any even-length simple path in the graph in which the colors of the edges in the first half of the path form the same sequence as the colors of the edges in the second half of the path. The Thue number of a graph is the minimum number of colors needed in any nonrepetitive coloring.^[1]

Variations on this concept involving vertex colorings or more general walks on a graph have been studied by several authors.^[2]

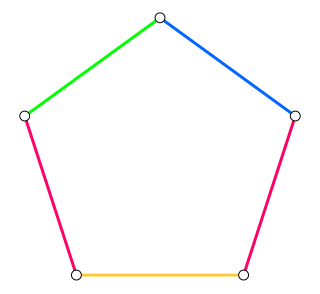
Example

Consider a pentagon, that is, a cycle ${\displaystyle C_{5}}$ of five vertices. If its edges are colored with two colors, some two adjacent edges will have the same color ${\displaystyle x}$; the path formed by those two edges will have the repetitive color sequence ${\displaystyle xx}$. If its edges are colored with three colors, one of the three colors will be used only once; the path of four edges formed by the other two colors will either have two consecutive edges or will form the repetitive color sequence ${\displaystyle xyxy}$. However, all repetitions can be avoided by using four colors, with one color repeated on two non-adjacent edges. Therefore, the Thue number of ${\displaystyle C_{5}}$ is four.^[1]

Results

Alon et al. use the Lovász local lemma to prove that the Thue number of any graph is at most quadratic in its maximum degree; they provide an example showing that for some graphs this quadratic dependence is necessary. In addition they show that the Thue number of a path of four or more vertices is exactly three, that the Thue number of any cycle is at most four, and that the Thue number of the Petersen graph is exactly five.^[1]

The cycles ${\displaystyle C_{5}}$, ${\displaystyle C_{7}}$, ${\displaystyle C_{9}}$, ${\displaystyle C_{10}}$, ${\displaystyle C_{14}}$, and ${\displaystyle C_{17}}$ have Thue number four.^[1] Resolving a conjecture of Alon et al., Currie showed that all other cycles have Thue number three.^[3]

Computational complexity

Testing whether a coloring has a repetitive path is in NP, so testing whether a coloring is nonrepetitive is in co-NP, and Manin showed that it is co-NP-complete. The problem of finding such a coloring belongs to ${\displaystyle \Sigma _{2}^{P}}$ in the polynomial hierarchy, and again Manin showed that it is complete for this level.^[4]