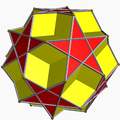
Truncated great dodecahedron

In geometry, the truncated great dodecahedron is a nonconvex uniform polyhedron, indexed as U₃₇. It has 24 faces (12 pentagrams and 12 decagons), 90 edges, and 60 vertices.^[1] It is given a Schläfli symbol t{5,5/2}.

Truncated great dodecahedron
Type	Uniform star polyhedron
Elements	F = 24, E = 90 V = 60 (χ = −6)
Faces by sides	12{5/2}+12{10}
Coxeter diagram
Wythoff symbol	2 5/2 | 5 2 5/3 | 5
Symmetry group	Ih, [5,3], *532
Index references	U37, C47, W75
Dual polyhedron	Small stellapentakis dodecahedron
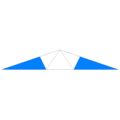
Vertex figure	10.10.5/2
Bowers acronym	Tigid

3D model of a truncated great dodecahedron

Related polyhedra

It shares its vertex arrangement with three other uniform polyhedra: the nonconvex great rhombicosidodecahedron, the great dodecicosidodecahedron, and the great rhombidodecahedron; and with the uniform compounds of 6 or 12 pentagonal prisms.

Nonconvex great rhombicosidodecahedron	Great dodecicosidodecahedron	Great rhombidodecahedron
Truncated great dodecahedron	Compound of six pentagonal prisms	Compound of twelve pentagonal prisms

This polyhedron is the truncation of the great dodecahedron:

The truncated small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 faces, 12 pentagons from the truncated vertices and 12 overlapping as (truncated pentagrams).

Name	Small stellated dodecahedron	Truncated small stellated dodecahedron	Dodecadodecahedron	Truncated great dodecahedron	Great dodecahedron
Coxeter-Dynkin diagram
Picture

---

Small stellapentakis dodecahedron

Small stellapentakis dodecahedron
Type	Star polyhedron
Face
Elements	F = 60, E = 90 V = 24 (χ = −6)
Symmetry group	Ih, [5,3], *532
Index references	DU37
dual polyhedron	Truncated great dodecahedron

3D model of a small stellapentakis dodecahedron

The small stellapentakis dodecahedron (or small astropentakis dodecahedron) is a nonconvex isohedral polyhedron. It is the dual of the truncated great dodecahedron. It has 60 intersecting triangular faces.

See also

• List of uniform polyhedra

References

1. Maeder, Roman. "37: truncated great dodecahedron". MathConsult.

Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208

External links

• Weisstein, Eric W. "Truncated great dodecahedron". MathWorld.
• Weisstein, Eric W. "Small stellapentakis dodecahedron". MathWorld.
• Uniform polyhedra and duals

Animated truncation sequence from {5⁄2, 5} to {5, 5⁄2}