Top Qs
Timeline
Chat
Perspective
Order-5 truncated pentagonal hexecontahedron
Convex polyhedron with 72 faces From Wikipedia, the free encyclopedia
Remove ads
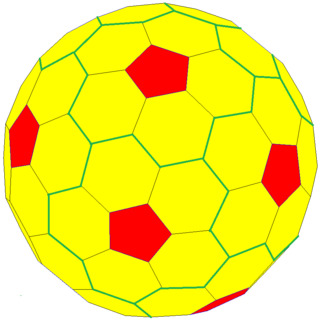
The order-5 truncated pentagonal hexecontahedron is a convex polyhedron with 72 faces: 60 hexagons and 12 pentagons triangular, with 210 edges, and 140 vertices. Its dual is the pentakis snub dodecahedron.
| Order-5 truncated pentagonal hexecontahedron | |
|---|---|
 | |
| Conway | t5gD or wD |
| Goldberg | {5+,3}2,1 |
| Fullerene | C140 |
| Faces | 72: 60 hexagons 12 pentagons |
| Edges | 210 |
| Vertices | 140 |
| Symmetry group | Icosahedral (I) |
| Dual polyhedron | Pentakis snub dodecahedron |
| Properties | convex, chiral |
| Net |  |
It is Goldberg polyhedron {5+,3}2,1 in the icosahedral family, with chiral symmetry. The relationship between pentagons steps into 2 hexagons away, and then a turn with one more step.
Remove ads
Construction
It is explicitly called a pentatruncated pentagonal hexecontahedron since only the valence-5 vertices of the pentagonal hexecontahedron are truncated.[2]
Its topology can be constructed in Conway polyhedron notation as t5gD and more simply wD as a whirled dodecahedron, reducing original pentagonal faces and adding 5 distorted hexagons around each, in clockwise or counter-clockwise forms. This picture shows its flat construction before the geometry is adjusted into a more spherical form. The snub can create a (5,3) geodesic polyhedron by k5k6.
Remove ads
Related polyhedra
The whirled dodecahedron creates more polyhedra by basic Conway polyhedron notation. The zip whirled dodecahedron makes a chamfered truncated icosahedron, and Goldberg (4,1). Whirl applied twice produces Goldberg (5,3), and applied twice with reverse orientations produces goldberg (7,0).
Remove ads
See also
- Truncated pentagonal icositetrahedron t4gC
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads