Snub (geometry)

In geometry, a snub is an operation applied to a polyhedron. The term originates from Kepler's names of two Archimedean solids, for the snub cube (cubus simus) and snub dodecahedron (dodecaedron simum).^[1]

The two snubbed Archimedean solids

Snub cube or Snub cuboctahedron

Snub dodecahedron or Snub icosidodecahedron

Two chiral copies of the snub cube, as alternated (red or green) vertices of the truncated cuboctahedron.

A snub cube can be constructed from a rhombicuboctahedron by rotating the 6 blue square faces until the 12 white square faces become pairs of equilateral triangle faces.

Transforming rhombicuboctahedron into a snub cube visualized.

In general, snubs have chiral symmetry with two forms: with clockwise or counterclockwise orientation. By Kepler's names, a snub can be seen as an expansion of a regular polyhedron: moving the faces apart, twisting them about their centers, adding new polygons centered on the original vertices, and adding pairs of triangles fitting between the original edges.

The terminology was generalized by Coxeter, with a slightly different definition, for a wider set of uniform polytopes.

Conway snubs

John Conway explored generalized polyhedron operators, defining what is now called Conway polyhedron notation, which can be applied to polyhedra and tilings. Conway calls Coxeter's operation a semi-snub.^[2]

In this notation, snub is defined by the dual and gyro operators, as s = dg, and it is equivalent to an alternation of a truncation of an ambo operator. Conway's notation itself avoids Coxeter's alternation (half) operation since it only applies for polyhedra with even-sided faces.

Snubbed regular figures

Forms to snub	Polyhedra			Euclidean tilings		Hyperbolic tilings
Names	Tetrahedron	Cube or octahedron	Icosahedron or dodecahedron	Square tiling	Hexagonal tiling or Triangular tiling	Heptagonal tiling or Order-7 triangular tiling
Images
Snubbed form Conway notation	sT	sC = sO	sI = sD	sQ	sH = sΔ	sΔ7
Image

In 4-dimensions, Conway suggests the snub 24-cell should be called a semi-snub 24-cell because, unlike 3-dimensional snub polyhedra are alternated omnitruncated forms, it is not an alternated omnitruncated 24-cell. It is instead actually an alternated truncated 24-cell.^[3]

Coxeter's snubs, regular and quasiregular

Snub cube, derived from cube or cuboctahedron

	Seed	Rectified r	Truncated t	Alternated h
Name	Cube	Cuboctahedron Rectified cube	Truncated cuboctahedron Cantitruncated cube	Snub cuboctahedron Snub rectified cube
Conway notation	C	CO rC	tCO trC or trO	htCO = sCO htrC = srC
Schläfli symbol	{4,3}	${\displaystyle {\begin{Bmatrix}4\\3\end{Bmatrix}}}$ or r{4,3}	${\displaystyle t{\begin{Bmatrix}4\\3\end{Bmatrix}}}$ or tr{4,3}	${\displaystyle ht{\begin{Bmatrix}4\\3\end{Bmatrix}}=s{\begin{Bmatrix}4\\3\end{Bmatrix}}}$ htr{4,3} = sr{4,3}
Coxeter diagram		or	or	or
Image

Coxeter's snub terminology is slightly different, meaning an alternated truncation, deriving the snub cube as a snub cuboctahedron, and the snub dodecahedron as a snub icosidodecahedron. This definition is used in the naming of two Johnson solids: the snub disphenoid and the snub square antiprism, and of higher dimensional polytopes, such as the 4-dimensional snub 24-cell, with extended Schläfli symbol s{3,4,3}, and Coxeter diagram .

A regular polyhedron (or tiling), with Schläfli symbol ${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$, and Coxeter diagram , has truncation defined as ${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$, and , and has snub defined as an alternated truncation ${\displaystyle ht{\begin{Bmatrix}p,q\end{Bmatrix}}=s{\begin{Bmatrix}p,q\end{Bmatrix}}}$, and . This alternated construction requires q to be even.

A quasiregular polyhedron, with Schläfli symbol ${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$ or r{p,q}, and Coxeter diagram or , has quasiregular truncation defined as ${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$ or tr{p,q}, and or , and has quasiregular snub defined as an alternated truncated rectification ${\displaystyle ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$ or htr{p,q} = sr{p,q}, and or .

For example, Kepler's snub cube is derived from the quasiregular cuboctahedron, with a vertical Schläfli symbol ${\displaystyle {\begin{Bmatrix}4\\3\end{Bmatrix}}}$, and Coxeter diagram , and so is more explicitly called a snub cuboctahedron, expressed by a vertical Schläfli symbol ${\displaystyle s{\begin{Bmatrix}4\\3\end{Bmatrix}}}$, and Coxeter diagram . The snub cuboctahedron is the alternation of the truncated cuboctahedron, ${\displaystyle t{\begin{Bmatrix}4\\3\end{Bmatrix}}}$, and .

Regular polyhedra with even-order vertices can also be snubbed as alternated truncations, like the snub octahedron, as ${\displaystyle s{\begin{Bmatrix}3,4\end{Bmatrix}}}$, , is the alternation of the truncated octahedron, ${\displaystyle t{\begin{Bmatrix}3,4\end{Bmatrix}}}$, and . The snub octahedron represents the pseudoicosahedron, a regular icosahedron with pyritohedral symmetry.

The snub tetratetrahedron, as ${\displaystyle s{\begin{Bmatrix}3\\3\end{Bmatrix}}}$, and , is the alternation of the truncated tetrahedral symmetry form, ${\displaystyle t{\begin{Bmatrix}3\\3\end{Bmatrix}}}$, and .

	Seed	Truncated t	Alternated h
Name	Octahedron	Truncated octahedron	Snub octahedron
Conway notation	O	tO	htO or sO
Schläfli symbol	{3,4}	t{3,4}	ht{3,4} = s{3,4}
Coxeter diagram
Image

Coxeter's snub operation also allows n-antiprisms to be defined as ${\displaystyle s{\begin{Bmatrix}2\\n\end{Bmatrix}}}$ or ${\displaystyle s{\begin{Bmatrix}2,2n\end{Bmatrix}}}$, based on n-prisms ${\displaystyle t{\begin{Bmatrix}2\\n\end{Bmatrix}}}$ or ${\displaystyle t{\begin{Bmatrix}2,2n\end{Bmatrix}}}$, while ${\displaystyle {\begin{Bmatrix}2,n\end{Bmatrix}}}$ is a regular n-hosohedron, a degenerate polyhedron, but a valid tiling on the sphere with digon or lune-shaped faces.

Snub hosohedra, {2,2p}

Image
Coxeter diagrams							... ...
Schläfli symbols	s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,12}	s{2,14}	s{2,16}...	s{2,∞}
	sr{2,2} ${\displaystyle s{\begin{Bmatrix}2\\2\end{Bmatrix}}}$	sr{2,3} ${\displaystyle s{\begin{Bmatrix}2\\3\end{Bmatrix}}}$	sr{2,4} ${\displaystyle s{\begin{Bmatrix}2\\4\end{Bmatrix}}}$	sr{2,5} ${\displaystyle s{\begin{Bmatrix}2\\5\end{Bmatrix}}}$	sr{2,6} ${\displaystyle s{\begin{Bmatrix}2\\6\end{Bmatrix}}}$	sr{2,7} ${\displaystyle s{\begin{Bmatrix}2\\7\end{Bmatrix}}}$	sr{2,8}... ${\displaystyle s{\begin{Bmatrix}2\\8\end{Bmatrix}}}$...	sr{2,∞} ${\displaystyle s{\begin{Bmatrix}2\\\infty \end{Bmatrix}}}$
Conway notation	A2 = T	A3 = O	A4	A5	A6	A7	A8...	A∞

The same process applies for snub tilings:

Triangular tiling Δ	Truncated triangular tiling tΔ	Snub triangular tiling htΔ = sΔ
{3,6}	t{3,6}	ht{3,6} = s{3,6}

Examples

Snubs based on {p,4}

Space	Spherical		Euclidean	Hyperbolic
Image
Coxeter diagram								...
Schläfli symbol	s{2,4}	s{3,4}	s{4,4}	s{5,4}	s{6,4}	s{7,4}	s{8,4}	...s{∞,4}

Quasiregular snubs based on r{p,3}

Conway notation	Spherical				Euclidean	Hyperbolic
Image
Coxeter diagram								...
Schläfli symbol	sr{2,3}	sr{3,3}	sr{4,3}	sr{5,3}	sr{6,3}	sr{7,3}	sr{8,3}	...sr{∞,3}
	${\displaystyle s{\begin{Bmatrix}2\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}3\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}4\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}5\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}6\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}7\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}8\\3\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}\infty \\3\end{Bmatrix}}}$
Conway notation	A3	sT	sC or sO	sD or sI	sΗ or sΔ

Quasiregular snubs based on r{p,4}

Space	Spherical		Euclidean	Hyperbolic
Image
Coxeter diagram								...
Schläfli symbol	sr{2,4}	sr{3,4}	sr{4,4}	sr{5,4}	sr{6,4}	sr{7,4}	sr{8,4}	...sr{∞,4}
	${\displaystyle s{\begin{Bmatrix}2\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}3\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}4\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}5\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}6\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}7\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}8\\4\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}\infty \\4\end{Bmatrix}}}$
Conway notation	A4	sC or sO	sQ

Nonuniform snub polyhedra

Nonuniform polyhedra with all even-valance vertices can be snubbed, including some infinite sets; for example:

Snub bipyramids sdt{2,p}

Snub square bipyramid
Snub hexagonal bipyramid

Snub rectified bipyramids srdt{2,p}

Snub antiprisms s{2,2p}

Image				...
Schläfli symbols	ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}...
	ssr{2,2} ${\displaystyle ss{\begin{Bmatrix}2\\2\end{Bmatrix}}}$	ssr{2,3} ${\displaystyle ss{\begin{Bmatrix}2\\3\end{Bmatrix}}}$	ssr{2,4} ${\displaystyle ss{\begin{Bmatrix}2\\4\end{Bmatrix}}}$	ssr{2,5}... ${\displaystyle ss{\begin{Bmatrix}2\\5\end{Bmatrix}}}$

Coxeter's uniform snub star-polyhedra

Snub star-polyhedra are constructed by their Schwarz triangle (p q r), with rational ordered mirror-angles, and all mirrors active and alternated.

Snubbed uniform star-polyhedra

s{3/2,3/2}	s{(3,3,5/2)}	sr{5,5/2}	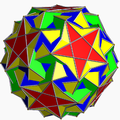s{(3,5,5/3)}	sr{5/2,3}
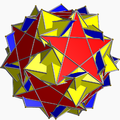sr{5/3,5}	s{(5/2,5/3,3)}	sr{5/3,3}	s{(3/2,3/2,5/2)}	s{3/2,5/3}

Coxeter's higher-dimensional snubbed polytopes and honeycombs

In general, a regular polychoron with Schläfli symbol ${\displaystyle {\begin{Bmatrix}p,q,r\end{Bmatrix}}}$, and Coxeter diagram , has a snub with extended Schläfli symbol ${\displaystyle s{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$, and .

A rectified polychoron ${\displaystyle {\begin{Bmatrix}p\\q,r\end{Bmatrix}}}$ = r{p,q,r}, and has snub symbol ${\displaystyle s{\begin{Bmatrix}p\\q,r\end{Bmatrix}}}$ = sr{p,q,r}, and .

Examples

Orthogonal projection of snub 24-cell

There is only one uniform convex snub in 4-dimensions, the snub 24-cell. The regular 24-cell has Schläfli symbol, ${\displaystyle {\begin{Bmatrix}3,4,3\end{Bmatrix}}}$, and Coxeter diagram , and the snub 24-cell is represented by ${\displaystyle s{\begin{Bmatrix}3,4,3\end{Bmatrix}}}$, Coxeter diagram . It also has an index 6 lower symmetry constructions as ${\displaystyle s\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}}$ or s{3^1,1,1} and , and an index 3 subsymmetry as ${\displaystyle s{\begin{Bmatrix}3\\3,4\end{Bmatrix}}}$ or sr{3,3,4}, and or .

The related snub 24-cell honeycomb can be seen as a ${\displaystyle s{\begin{Bmatrix}3,4,3,3\end{Bmatrix}}}$ or s{3,4,3,3}, and , and lower symmetry ${\displaystyle s{\begin{Bmatrix}3\\3,4,3\end{Bmatrix}}}$ or sr{3,3,4,3} and or , and lowest symmetry form as ${\displaystyle s\left\{{\begin{array}{l}3\\3\\3\\3\end{array}}\right\}}$ or s{3^1,1,1,1} and .

A Euclidean honeycomb is an alternated hexagonal slab honeycomb, s{2,6,3}, and or sr{2,3,6}, and or sr{2,3^[3]}, and .

Another Euclidean (scaliform) honeycomb is an alternated square slab honeycomb, s{2,4,4}, and or sr{2,4^1,1} and :

The only uniform snub hyperbolic uniform honeycomb is the snub hexagonal tiling honeycomb, as s{3,6,3} and , which can also be constructed as an alternated hexagonal tiling honeycomb, h{6,3,3}, . It is also constructed as s{3^[3,3]} and .

Another hyperbolic (scaliform) honeycomb is a snub order-4 octahedral honeycomb, s{3,4,4}, and .

See also

• Snub polyhedron

Polyhedron operators

• v
• t
• e

Seed	Truncation	Rectification	Bitruncation	Dual	Expansion	Omnitruncation	Alternations
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q} s{q,p}	ht012{p,q} sr{p,q}