Top Qs
Timeline
Chat
Perspective
Chamfer (geometry)
Geometric operation which truncates the edges of polyhedra From Wikipedia, the free encyclopedia
Remove ads
In geometry, a chamfer or edge-truncation is a topological operator that modifies one polyhedron into another. It separates the faces by reducing them, and adds a new face between each two adjacent faces (moving the vertices inward). Oppositely, similar to expansion, it moves the faces apart outward, and adds a new face between each two adjacent faces; but contrary to expansion, it maintains the original vertices.
This article needs additional citations for verification. (March 2025) |
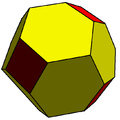
Unchamfered, slightly chamfered, and chamfered cube
Historical crystal models of slightly chamfered Platonic solids
For a polyhedron, this operation adds a new hexagonal face in place of each original edge.
In Conway polyhedron notation, chamfering is represented by the letter "c". A polyhedron with e edges will have a chamfered form containing 2e new vertices, 3e new edges, and e new hexagonal faces.
Remove ads
Platonic solids
Summarize
Perspective
Left to right: chamfered tetrahedron, cube, octahedron, dodecahedron, and icosahedron
Chamfers of five Platonic solids are described in detail below.

- chamfered tetrahedron or alternated truncated cube: from a regular tetrahedron, this replaces its six edges with congruent flattened hexagons; or alternately truncating a cube, replacing four of its eight vertices with congruent equilateral-triangle faces. This is an example of Goldberg polyhedron GPIII(2,0) or {3+,3}2,0, containing triangular and hexagonal faces. Its dual is the alternate-triakis tetratetrahedron.[2]
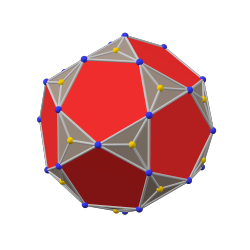
- chamfered cube: from a cube, the resulting polyhedron has twelve hexagonal and six square centrally symmetric faces, a zonohedron.[3] This is also an example of the Goldberg polyhedron GPIV(2,0) or {4+,3}2,0. Its dual is the tetrakis cuboctahedron. A twisty puzzle of the DaYan Gem 7 is the shape of a chamfered cube.[4]
- chamfered octahedron or tritruncated rhombic dodecahedron: from a regular octahedron by chamfering,[5] or by truncating the eight order-3 vertices of the rhombic dodecahedron, which become congruent equilateral triangles, and the original twelve rhombic faces become congruent flattened hexagons. It is a Goldberg polyhedron GPV(2,0) or {5+,3}2,0. Its dual is triakis cuboctahedron.[2]
pentakis icosidodecahedron and triakis icosidodecahedron
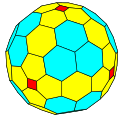
- chamfered dodecahedron: by chamfering a regular dodecahedron, the resulting polyhedron has 80 vertices, 120 edges, and 42 faces: 12 congruent regular pentagons and 30 congruent flattened hexagons. GPV(2,0) = {5+,3}2,0. The structure resembles C60 fullerene.[6] Its dual is the pentakis icosidodecahedron.[2]
- chamfered icosahedron or tritruncated rhombic triacontahedron: by chamfering a regular icosahedron, or truncating the twenty order-3 vertices of the rhombic triacontahedron. The hexagonal faces of the cI can be made equilateral, but not regular, with a certain depth of truncation. Its dual is the triakis icosidodecahedron.[2]
Remove ads
Regular tilings
 Square tiling, Q {4,4} |
 Triangular tiling, Δ {3,6} |
 Hexagonal tiling, H {6,3} |
 Rhombille, daH dr{6,3} |
 |
 |
 |
 |
| cQ | cΔ | cH | cdaH |
Relation to Goldberg polyhedra
The chamfer operation applied in series creates progressively larger polyhedra with new faces, hexagonal, replacing the edges of the current one. The chamfer operator transforms GP(m,n) to GP(2m,2n).
A regular polyhedron, GP(1,0), creates a Goldberg polyhedra sequence: GP(1,0), GP(2,0), GP(4,0), GP(8,0), GP(16,0)...
The truncated octahedron or truncated icosahedron, GP(1,1), creates a Goldberg sequence: GP(1,1), GP(2,2), GP(4,4), GP(8,8)...
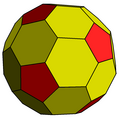
A truncated tetrakis hexahedron or pentakis dodecahedron, GP(3,0), creates a Goldberg sequence: GP(3,0), GP(6,0), GP(12,0)...
See also
References
Sources
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads