Two-point equidistant projection

The two-point equidistant projection or doubly equidistant projection is a map projection first described by Hans Maurer in 1919 and Charles Close in 1921.^[1][2] It is a generalization of the much simpler azimuthal equidistant projection. In this two-point form, two locus points are chosen by the mapmaker to configure the projection. Distances from the two loci to any other point on the map are correct: that is, they scale to the distances of the same points on the sphere.

Two-point equidistant projection of Eurasia. All distances are correct from the two points (45°N, 40°E) and (30°N, 110°E).

Two-point equidistant projection of the entire world with Tissot's indicatrix of deformation. The two points are Rome, Italy and Luoyang, China.

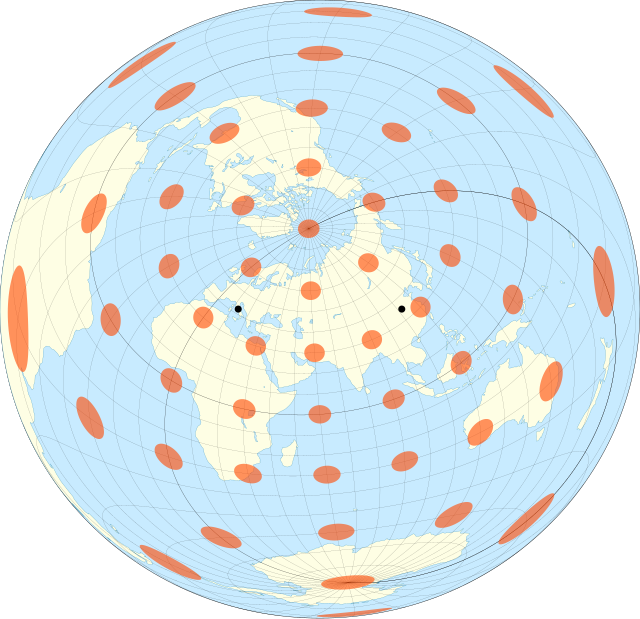
The two-point equidistant projection maps a family of confocal spherical conics onto two families of planar ellipses and hyperbolas.^[3]

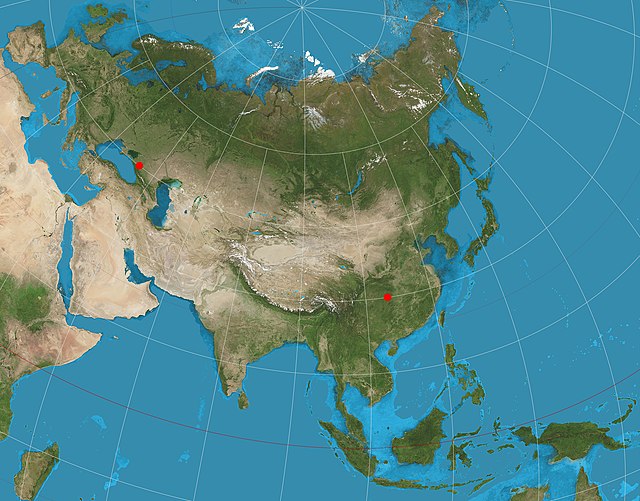
The projection has been used for all maps of the Asian continent by the National Geographic Society atlases since 1959,^[4] though its purpose in that case was to reduce distortion throughout Asia rather than to measure from the two loci.^[5] The projection sometimes appears in maps of air routes. The Chamberlin trimetric projection is a logical extension of the two-point idea to three points, but the three-point case only yields a sort of minimum error for distances from the three loci, rather than yielding correct distances. Tobler extended this idea to arbitrarily large number of loci by using automated root-mean-square minimization techniques rather than using closed-form formulae.^[6]

The projection can be generalized to an ellipsoid of revolution by using geodesic distance.^[7]

See also

• List of map projections
• Chamberlin trimetric projection
• 3D projection