Top Qs
Timeline
Chat
Perspective
Tzolkinex
Eclipse cycle equal to a period of two saros cycles From Wikipedia, the free encyclopedia
Remove ads
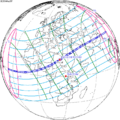
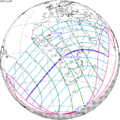
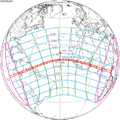
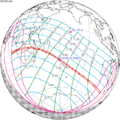
The tzolkinex is an eclipse cycle equal to a period of two saros (13,170.636 days) minus one inex (10,571.946 days). As consecutive eclipses in an inex series belongs to the next consecutive saros series, each consecutive tzolkinex belongs to the previous saros series.
This article needs additional citations for verification. (March 2025) |
The tzolkinex is equal to 2598.691 days (about 7 years, 1 month and 12 days). It is related to the tritos in that a period of one tritos plus one tzolkinex is exactly equal to one saros. It is also related to the inex in that a period of one inex plus one tzolkinex is exactly equal to two saros.
It corresponds to:
- 88 synodic months
- 95.49723 draconic months
- 7.49723 eclipse years (15 eclipse seasons)
- 94.31081 anomalistic months.
Because of the non-integer number of anomalistic month each eclipse varies in type, i.e. total vs. annular, and greatly varies in length. From remainder of 0.31081, being near 1⁄3, every third tzolkinex comes close to an even number of anomalistic months, but occurs during a different season, and in the opposite hemisphere, thus they may be of the same type (annular vs. total) but otherwise do not have a similar character.
Remove ads
Details
Summarize
Perspective
It was first studied by George van den Bergh (1951). The name was suggested by Felix Verbelen (2001) because its length is nearly 10 Tzolk'ins (260-day periods).[1]
It alternates hemispheres with each cycle, occurring at alternating nodes, each successive occurrence is one saros less than the last.
Remove ads
See also
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads