Top Qs
Timeline
Chat
Perspective
Up to
Mathematical statement of uniqueness, except for an equivalent structure From Wikipedia, the free encyclopedia
Remove ads
Two mathematical objects a and b are called "equal up to an equivalence relation R"
- if a and b are related by R, that is,
- if aRb holds, that is,
- if the equivalence classes of a and b with respect to R are equal.
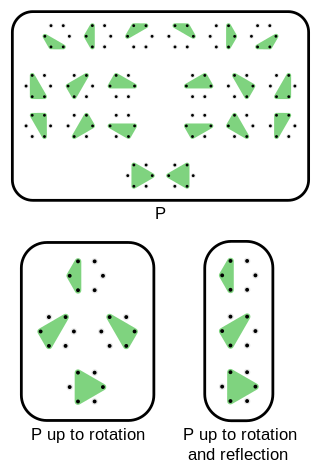
This figure of speech is mostly used in connection with expressions derived from equality, such as uniqueness or count. For example, "x is unique up to R" means that all objects x under consideration are in the same equivalence class with respect to the relation R.
Moreover, the equivalence relation R is often designated rather implicitly by a generating condition or transformation. For example, the statement "an integer's prime factorization is unique up to ordering" is a concise way to say that any two lists of prime factors of a given integer are equivalent with respect to the relation R that relates two lists if one can be obtained by reordering (permuting) the other.[1] As another example, the statement "the solution to an indefinite integral is sin(x), up to addition of a constant" tacitly employs the equivalence relation R between functions, defined by fRg if the difference f−g is a constant function, and means that the solution and the function sin(x) are equal up to this R. In the picture, "there are 4 partitions up to rotation" means that the set P has 4 equivalence classes with respect to R defined by aRb if b can be obtained from a by rotation; one representative from each class is shown in the bottom left picture part.
Equivalence relations are often used to disregard possible differences of objects, so "up to R" can be understood informally as "ignoring the same subtleties as R ignores". In the factorization example, "up to ordering" means "ignoring the particular ordering".
Further examples include "up to isomorphism", "up to permutations", and "up to rotations", which are described in the Examples section.
In informal contexts, mathematicians often use the word modulo (or simply mod) for similar purposes, as in "modulo isomorphism".
Objects that are distinct up to an equivalence relation defined by a group action, such as rotation, reflection, or permutation, can be counted using Burnside's lemma or its generalization, Pólya enumeration theorem.
Remove ads
Examples
Summarize
Perspective
Tetris

Consider the seven Tetris pieces (I, J, L, O, S, T, Z), known mathematically as the tetrominoes. If you consider all the possible rotations of these pieces — for example, if you consider the "I" oriented vertically to be distinct from the "I" oriented horizontally — then you find there are 19 distinct possible shapes to be displayed on the screen. (These 19 are the so-called "fixed" tetrominoes.[2]) But if rotations are not considered distinct — so that we treat both "I vertically" and "I horizontally" indifferently as "I" — then there are only seven. We say that "there are seven tetrominoes, up to rotation". One could also say that "there are five tetrominoes, up to rotation and reflection", which accounts for the fact that L reflected gives J, and S reflected gives Z.
Eight queens

In the eight queens puzzle, if the queens are considered to be distinct (e.g. if they are colored with eight different colors), then there are 3709440 distinct solutions. Normally, however, the queens are considered to be interchangeable, and one usually says "there are 3,709,440 / 8! = 92 unique solutions up to permutation of the queens", or that "there are 92 solutions modulo the names of the queens", signifying that two different arrangements of the queens are considered equivalent if the queens have been permuted, as long as the set of occupied squares remains the same.
If, in addition to treating the queens as identical, rotations and reflections of the board were allowed, we would have only 12 distinct solutions "up to symmetry and the naming of the queens". For more, see Eight queens puzzle § Solutions.
Polygons
The regular n-gon, for a fixed n, is unique up to similarity. In other words, the "similarity" equivalence relation over the regular n-gons (for a fixed n) has only one equivalence class; it is impossible to produce two regular n-gons which are not similar to each other.
Group theory
In group theory, one may have a group G acting on a set X, in which case, one might say that two elements of X are equivalent "up to the group action"—if they lie in the same orbit.
Another typical example is the statement that "there are two different groups of order 4 up to isomorphism", or "modulo isomorphism, there are two groups of order 4". This means that, if one considers isomorphic groups "equivalent", there are only two equivalence classes of groups of order 4, prototypically the cyclic group of order 4 and the Klein four-group.
Nonstandard analysis
A hyperreal x and its standard part st(x) are equal up to an infinitesimal difference.
Remove ads
See also
Look up up to in Wiktionary, the free dictionary.
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
